
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ПОТОКИ СОБЫТИЙ. ХАРАКТЕРИСТИКИ ПОТОКОВПотоком событий называется последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени. Важной характеристикой потока событий является его интенсивность λ - среднее число событий, приходящихся на единицу времени. Интенсивность потока может быть постоянной (λ = const) или переменной, т.е. зависящей от времени t, например, поток машин на автостраде днем интенсивнее, чем ночью. Поток событий называется регулярным, если события следуют одно за другим через определенные, равные промежутки времени (например, выход изделий из производящего автомата). На практике чаще встречаются потоки нерегулярные, со случайными интервалами. Поток событий называется стационарным, если его вероятностные характеристики не зависят от времени. В частности средняя интенсивность λ стационарного потока должна быть постоянной. Поток событий называется потоком без последействия, если для любых двух непересекающихся участков времени t1 и t2 число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой. По сути, это означает, что события, образующие поток, появляются в те или иные моменты времени независимо друг от друга, и каждое порождается своими собственными причинами. Например, поток пассажиров, входящих в метро, практически не имеет последействия. А вот поток пассажиров, выходящих из метро, - поток с последействием, т.к. его интенсивность зависит от графика движения поездов метро. Поток событий называется ординарным, если события в нем появляются поодиночке, а не группами, по нескольку событий сразу. Если поток ординарен, то вероятностью попадания на малый участок времени Δt двух и более событий можно пренебречь.  Поток событий называется простейшим (пуассоновским), если он обладает сразу тремя свойствами: стационарен, ординарен и не имеет последействия. Название «простейший» обусловлено тем, что процессы, связанные с такими потоками, имеют наиболее простое математическое описание. Между прочим, самый простой на первый взгляд, регулярный поток не является простейшим, т.к. обладает последействием: моменты появления событий в таком потоке связаны жесткой функциональной зависимостью. Без специальных усилий по поддержанию его регулярности такой поток существовать не может. Всякая СМО предназначена для обслуживания потока заявок, поступающих в случайные моменты времени. Обслуживание заявки продолжается какое-то, вообще говоря, случайное время Tобс, после чего канал освобождается и готов к приему следующей заявки. Случайный характер потока заявок и времен их обслуживания приводит к тому, что в определенные моменты времени на входе СМО скапливается излишне большое число заявок (они либо становятся в очередь, либо покидают СМО необслуженными), в другие же периоды времени СМО будет работать с недогрузкой или вообще простаивать.
Рассмотрим одноканальную СМО с неограниченной очередью, показанную на рисунке
Если обозначить среднее время пребывания требований в очереди w рассматривать СМО как очередь q, то, используя формулу Литтла можно найти среднее количество требований в очереди:
Если обозначить среднее время обслуживания в устройстве и рассматривать СМО как устройство S, то, используя формулу Литтла можно найти среднее количество требований в устройстве:
Всегда имеет место уравнение T = w+, где Т - среднее время пребывания требований в СМО с одним устройством обслуживания. Коэффициент загрузки определяет, какую часть времени устройство было занято на протяжении всего времени наблюдения за СМО. Для обозначения СМО используются три параметра для первых параметров: X/Y/Z, где X - распределение времени поступления; Y – распределение времени обслуживания; Z- число обслуживающих устройств. В теории СМО некоторые аналитические решения были получены для систем вида D/D/l, M/M/1 и М/G/l. Для других значений параметров систем обслуживания аналитические решения не были получены, то есть эта проблема мотивирует использование моделирования. Самая известная модель - это так называемая СМО типа М/М/1, где М - марковские процессы распределения времени поступления и обслуживания с одним устройством. Например, в системе М/М/1 время между двумя поступлениями в систему требований и время обслуживания имеют экспоненциальные распределения. Такая СМО иногда используется как модель для одного процессора компьютерной системы или как стандартное устройство ввода-вывода (например, магнитный диск). Система D/D/1 - детерминированная система, тогда как D/M/1 – смешанная. Если о системе мало известно, это обозначается какG/G/m, то есть система с произвольными распределениями и m устройствами. Изучая любую систему, важно оценить характер ее рабочей нагрузки (например, при моделировании компьютерной системы важно знать: когда новые программы (задачи) поступают в систему; сколько времени нужно процессору для выполнения любой из них; как часто программа обращается к устройству ввода-вывода). Этот процесс можно отобразить графиком работы системы (графический метод моделирования), на котором показаны входы задач в систему, ресурсы к которым они обращаются, как долго задачи их используют и т.д. Если описанный сценарий зафиксирован соответствующим графиком и часто возникает в моделируемой системе, то тогда он целиком отвечает выборке, которая получена методом измерений при наблюдении за работой компьютера. Тем не менее, моделирование при использовании такого описания рабочей нагрузки только воссоздает результаты работы этого специфического сценария. Этого недостаточно для выполнения системой других сценариев. Даже незначительное несоответствие заданному сценарию может привести к драматическим последствиям работы компьютера. Часто рабочая нагрузка на систему определяется одним или несколькими распределениями вероятностей в отличие от заданных сценариев. Например, можно бросать монету каждые 15 мин на протяжении операции исследования системы, и если монета падает лицевой стороной, то новая задача поступает в систему в этот момент времени. Если монета падает обратной стороной, то никакая задача не поступает в систему. Это пример метода розыгрыша случайной величины (метод Монте-Карло), который используется для моделирования вероятностных систем. В компьютерном моделировании «бросание монеты» можно генерировать методом случайных чисел. Если выявлены статистические закономерности и используются соответствующие распределения вероятностей для определения рабочей нагрузки на систему, а также применяются соответствующие статистические методы анализа результатов моделирования, то полученные результаты относятся к более широкому диапазону рабочих нагрузок, чем подход с использованием определенного сценария.
ВЫВОД ФОРМУЛ ЛИТТЛА Выведем одну важную формулу, связывающую (для предельного стационарного режима) среднее число заявок Lсист, находящихся в системе массового обслуживания (т. е. обслуживаемых или стоящих в очереди), и среднее время пребывания заявки в системе Wсист. Рассмотрим любую СМО (одноканальную, многоканальную, марковскую, немарковскую, с неограниченной или с ограниченной очередью) и связанные с нею 2 потока событий: поток заявок, прибывающих в СМО, и поток заявок, покидающих СМО. Если в системе установился предельный, стационарный режим, то среднее число заявок, прибывающих в СМО за единицу времени, равно среднему числу заявок, покидающих ее: оба потока имеют одну и ту же интенсивность λ. Обозначим: Х(t)—число заявок, прибывших в СМО до момента t, Y(t) — число заявок, покинувших СМО до момента t.
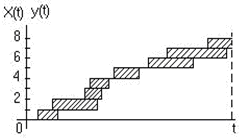
И та, и другая функции являются случайными и меняются скачком (увеличиваются на единицу) в моменты приходов заявок (X(t)) и уходов заявок (У(t)). Вид функций X(t) и У(t) показан на рис.1; обе линии — ступенчатые, верхняя — X(t), нижняя — Y(t). Очевидно, что для любого момента t их разность Z(t) = Х(t) —Y(t) есть не что иное, как число заявок, находящихся в СМО. Когда линии X(t) и У(t) сливаются, в системе нет заявок. Рассмотрим очень большой промежуток времени Т (мысленно продолжив график далеко за пределы чертежа) и вычислим для него среднее число заявок, находящихся в СМО. Оно будет равно интегралу от функции Z(t) на этом промежутке, деленному на длину интервала Т: Но этот интеграл представляет собой не что иное, как площадь фигуры, заштрихованной на рис.1. Фигура состоит из прямоугольников, каждый из которых имеет высоту, равную единице, и основание, равное времени пребывания в системе соответствующей заявки (первой, второй и т. д.). Обозначим эти времена t1, t2 ,... Правда, в конце промежутка Т некоторые прямоугольники войдут в заштрихованную фигуру не полностью, а частично, но при достаточно большом Т эти мелочи не будут играть роли. Таким образом, можно считать, что Но величина Т λ есть не что иное, как среднее число заявок, пришедших за время Т. Если мы разделим сумму всех времен t на среднее число заявок, то получим среднее время пребывания заявки в системе Wсист. Итак, L= λ W, откуда Wсист = Lсист / λ. (1) Это и есть замечательная формула Литтла: для любой СМО, при любом характере потока заявок, при любом распределении времени обслуживания, при любой дисциплине обслуживания среднее время пребывания заявки в системе равно среднему числу заявок в системе, деленному на интенсивность потока заявок. Точно таким же образом выводится вторая формула Литтла, связывающая среднее время пребывания заявки в очереди Wоч и среднее число заявок в очереди Lоч: Wоч =Lоч / λ. Для вывода достаточно вместо нижней линии из рис.1 взять функцию U(t) — количество заявок, ушедших до момента Т не из системы, а из очереди (если заявка, пришедшая в систему, не становится в очередь, а сразу идет под обслуживание, можно все же считать, что она становится в очередь, но находится в ней нулевое время). Формулы Литтла играют большую роль в теории массового обслуживания.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 796. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

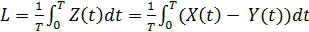
 , где сумма распространяется на все заявки, пришедшие за время Т. Разделим и умножим правую часть на интенсивность λ:
, где сумма распространяется на все заявки, пришедшие за время Т. Разделим и умножим правую часть на интенсивность λ:  .
.