
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ВЕРОЯТНОСТИ СОСТОЯНИЙ. ОБЩЕЕ ПРАВИЛО СОСТАВЛЕНИЯ УРАВНЕНИЙ КОЛМОГОРОВАРассмотрим стационарный случайный процесс с дискретным состоянием и непрерывным временем. Все переходы из состояния в состояние происходят под действием каких-то потоков событий. Если все эти потоки простейшие, то процесс, протекающий в системе, можно считать мартовским. Пусть система S имеет n возможных состояний Задача: составить уравнения, описывающие вероятности состояний поведения данной системы. Правило составлений уравнений Колмогорова: В левой части каждого из уравнений стоит производная по времени от вероятности данного состояния. В правой части стоит сумма произведений всех состояний, из которых возможен переход в данное состояние, на интенсивности соответствующих потоков событий минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного состояния. Например, для графа состояний, приведенного на рис. 1, уравнения Колмогорова имеют вид:
Т.к. в правой части системы каждое слагаемое входит 1 раз со знаком
Следовательно, одно из уравнений системы можно отбросить и заменить уравнением (1.2.1). Чтобы получить конкретное решение надо знать начальные условия, т.е. значения вероятностей в начальный момент времени.
МАРКОВСКИЙ ПРОЦЕСС Процесс, протекающий в физической системе, называется марковским (или процессом без последействия), если для каждого момента времени вероятность любого состояния системы в будущем зависит только от состояния системы в настоящий момент  Рассмотрим элементарный пример марковского случайного процесса. По оси абсцисс
Схема возможных переходов для этого процесса показана на рис
Покажем, что этот процесс - марковский. Действительно, представим себе, что в какой-то момент времени |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 337. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


 .
.
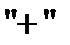 и 1 раз со знаком
и 1 раз со знаком 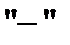 , то, складывая все
, то, складывая все  уравнений, получим, что
уравнений, получим, что ,
, ,
,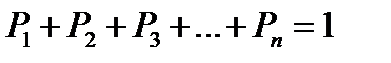 . (1.2.1)
. (1.2.1)



 и не зависит от того, каким образом система пришла в это состояние.
и не зависит от того, каким образом система пришла в это состояние. случайным образом перемещается точка
случайным образом перемещается точка  . В момент времени
. В момент времени 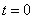 точка
точка  и остается там в течение одной секунды. Через секунду бросается монета; если выпал герб - точка
и остается там в течение одной секунды. Через секунду бросается монета; если выпал герб - точка 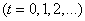 и счетным множеством состояний
и счетным множеством состояний

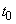 система находится, например, в состоянии
система находится, например, в состоянии  - на одну единицу правее начала координат. Возможные положения точки через единицу времени будут
- на одну единицу правее начала координат. Возможные положения точки через единицу времени будут  и
и 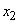 с вероятностями 1/2 и 1/2; через две единицы -
с вероятностями 1/2 и 1/2; через две единицы -  ,
,  с вероятностями 1/4, ½, 1/4 и так далее. Очевидно, все эти вероятности зависят только от того, где находится точка в данный момент
с вероятностями 1/4, ½, 1/4 и так далее. Очевидно, все эти вероятности зависят только от того, где находится точка в данный момент