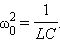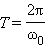СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ

1 Ушаков П.А. Цепи и сигналы электросвязи: учебник для студ. учреждений сред.проф. образования. – М.: Издательский центр «Академия», 2010. – 352 с. ISBN 978-5-7695-5669-2

2 Каганов В.И. Радиотехнические цепи и сигналы. Компьютеризированный курс. Учебное пособие. – М.: ФОРУМ, 2011. – 432 с. ISBN5-8199-0151-7

ЛАБОРАТОРНАЯ РАБОТА 1 ИЗМЕРЕНИЕ ПАРАМЕТРОВ СВОБОДНЫХ КОЛЕБАНИЙВ КОНТУРЕ

Цель работы: Ознакомиться с методикой получения свободных колебаний. Изучить связь параметров контура с характером свободных колебаний.

Студент должен:

знать:

- параметры и характеристика свободных колебаний;

- виды потерь в реальном колебательном контуре;

- условия возникновения колебаний;

- математическое описание тока и напряжения;

- способы графического представления тока и напряжения;

уметь:

- решать задачи по определению параметров и характеристик свободных колебаний;

- снимать временные диаграммы напряжений на элементах контура;

- анализировать результаты измерений и расчетов.

Приборы и оборудование:ПК, программное обеспечение EWBMultisim12.0, MathCad 12. Виртуальный генератор импульсов, осциллограф.

ЗАДАНИЕ ДЛЯ ВЫПОЛНЕНИЯ

Осуществить компьютерное моделирование свободных затухающих колебаний в контуре и установить влияние параметров контура на параметры затухающих колебаний

ОСНОВНЫЕ ПОЛОЖЕНИЯ

В электрических цепях, так же как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания. Простейшей электрической системой, способной совершать свободные колебания, является последовательный RLC-контур (рисунок 1).

Рисунок 1 – Последовательный RLC-контур

Когда ключ K находится в положении 1, конденсатор заряжается до напряжения ε. После переключения ключа в положение 2 начинается процесс разрядки конденсатора через резистор R и катушку индуктивности L. При определенных условиях этот процесс может иметь колебательный характер.

Закон Ома для замкнутой RLC-цепи, не содержащей внешнего источника тока, записывается в виде:

(1)

где U = q/C – напряжение на конденсаторе,

       q – заряд конденсатора,

       J = dq/dt– ток в цепи.

В правой части этого соотношения стоит ЭДС самоиндукции катушки. Если в качестве переменной величины выбрать заряд конденсатора q (t), уравнение, описывающее свободные колебания в RLC-контуре, может быть приведено к следующему виду:

(2)

Рассмотрим сначала случай, когда в контуре нет потерь электромагнитной энергии (R = 0). Тогда

(3)

Здесь принято обозначение:

(4)

Уравнение (3) описывает свободные колебания в LC-контуре в отсутствие затухания. На рисунке приведены графики изменения заряда q(t) конденсатора, а также графики тока J (t) за один период колебаний.

Рисунок 2 – График изменения заряда q (t) конденсатора и график изменения тока J (t) за один период колебаний

В отсутствие затухания свободные колебания в электрическом контуре являются гармоническими, то есть происходят по закону

Параметры L и C колебательного контура определяют только собственную частоту свободных колебаний

(6)

Амплитуда q₀ и начальная фаза φ₀ определяются начальными условиями, то есть тем способом, с помощью которого система была выведена из состояния равновесия. При свободных колебаниях происходит периодическое превращение электрической энергии W_э, запасенной в конденсаторе, в магнитную энергию W_м катушки и наоборот. Если в колебательном контуре нет потерь энергии, то полная электромагнитная энергия системы остается неизменной:

(7)

Все реальные контуры содержат электрическое сопротивление R. Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в джоулево тепло, и колебания становятся затухающими (рисунок 7.3).

Рисунок 3 – Затухающие колебания в контуре

Затухающие колебания в электрическом контуре аналогичны затухающим колебаниям груза на пружине при наличии вязкого трения, когда сила трения изменяется прямо пропорционально скорости тела: F_тр = – βυ. Коэффициент β в этой формуле аналогичен сопротивлению R электрического контура. Уравнение свободных колебаний в контуре при наличии затухания имеет вид

(8)

Физическая величина δ = R / 2L называется коэффициентом затухания. Решением этого дифференциального уравнения является функция

(9)

которая содержит множитель exp (–δt), описывающий затухание колебаний.

Скорость затухания зависит от электрического сопротивления R контура.

Интервал времени, в течение которого амплитуда колебаний уменьшается в e ≈ 2,7 раза, называется временем затухания.

Затухание контура d – это отношение активного сопротивления контура к его волновому сопротивлению.

(10)

Добротность контура – это величина обратная зату­ханию.

Добротность Q колебательной системы (RLC-контура):

(11)

где N – число полных колебаний, совершаемых системой за время затухания τ. Добротности Q любой колебательной системы, способной совершать свободные колебания, может быть дано энергетическое определение:

(12)

Добротность электрических контуров, применяемых в радиотехнике, обычно порядка нескольких десятков и даже сотен.

Следует отметить, что собственная частота ω свободных колебаний в контуре с не очень высокой добротностью несколько меньше собственной частоты ω₀ идеального контура с теми же значениями L и C. Но при Q ≥ (5÷10) этим различием можно пренебречь.

Затухание колебаний происходит по закону

где U_m0 – амплитуда колебаний в начальный момент времени,

       e – основание натуральных логарифмов; 

       t– текущее время;

       δ=r/2L – коэффициент затухания.

Логарифмический декремент затухания θ- натуральный логарифм отношения двух соседних амплитуд, отличающихся на период колебаний Т0

(14)

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1 Собрать схему исследования, приведенную на рисунке 4, подключив измерительные приборы: осциллограф, вольтметр, генератор прямоугольных импульсов.

Рисунок 4 – Схема исследования

2 Установить параметры. Подать напряжение питания 10В. Вклю­чить импульсный генератор, установив частоту колебаний 8 кГц, длительность положительного прямоугольного импульса 100 мкс и амплитуду импульса 5В.

3 Рассчитать параметры колебаний. По данной величине индуктивности контура и конденсатора рассчитать периоды и частоты собственных колебаний для трех значений емкости контура: минимальной, средней и максимальной по формулам (4) и (6). Результаты расчета занести в таблицу 1.

Таблица 1 – Практические результаты

4 Снять осциллограммы напряжений. Включить осциллограф, получить на его экране устой­чивое изображение свободных колебаний для трех значений емкости контура. С помощью осциллографа измерить период свободных колебаний. Результаты измерений занести в таблицу 1.   

5 Произвести измерение параметров затухающих коле­баний контура. Для этого получить устойчивое изображение колебаний на экране осциллографа, зарисовать их, измерить с по­мощью осциллографа три соседних амплитуды колебаний Результаты измерений занести в таблицу 2. По данным измерений вычислить логарифмический декремент затухания, добротность и затухание контура, выражение (14). Указанные измерения и вычисления произвести при следующих условиях:

а) при минимальном значении емкости и отключенном реостате;

б) при минимальном значении емкости контура и включенном добавочном резисторе (реостате) R=100 Ом;

в) при максимальном значении емкости контура и отклю­ченном добавочном резисторе;

г) при максимальном значении емкости контура и включен­ном добавочном резисторе.

Результаты измерений и вычислений занести в таблицу 2.

Таблица 2 – Результаты измерений параметров затухающих колебаний.