
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Анализ основных принципов оптимальности, форм компромиссов и методов решения на основе понятий стабильности и эффективностиВ соответствии с понятиями стабильности и эффективности многие из существующих принципов оптимальности связаны с тремя базовыми: оптимальность на основе гарантированных подходов, коалиционного равновесия и кооперативных соглашений. Принцип оптимальности на основе гарантированных решений базируется на исследовании максиминных и минимаксных задач и равновесных (седловых) решений. Принцип оптимальности на основе коалиционного равновесия связан с игровыми подходами в виде скалярного Нэш-равновесия, векторных равновесий (в частности, «сильного» равновесия, векторного Нэш-равновесия, Принцип оптимальности на основе кооперативных соглашений содержит два основных взаимосвязанных направления: векторная оптимизация для определения множества Парето-решений (без структурных свойств ММС)(скаляризация, лексикографическая оптимизация, пороговая оптимизация и принцип сложности, оптимизация на основе конусов доминирования, среднеквадратическая оптимизация и др.) и исследование кооперативной игры в форме характеристической функции (с элементами учета структуры ММС: коллективной и индивидуальной рациональности и т.д.) (С-ядро, Н-ядро, решение Нэймана–Моргенштерна (Н-М-решение), решение на основе вектора дележа Шепли, с учетом и без учета платежей и др.). Причем решаются задачи получения множества Парето и выбора кооперативного (эффективного) компромисса (принцип сложности, Известны также определенные результаты по комбинированию стабильных и эффективных решений (некоторые условия их совпадения, методы доминирования, некоторые методы комбинирования Парето-решений, максиминных решений, Нэш-решений, предостережений типа «угроз-контругроз», работы по анализу условий вступления в коалицию и др.).  Обзор существующих подходов и методов приведен в [54] и разделен по главам. Кроме того, рекомендуются авторские рефераты некоторых фундаментальных и обзорных работ по неантагонистическим играм с анализом и дополнениями: Э.М. Вайсборда–В.Н. Жуковского [32], Э.Й. Вилкаса [39], Ю.Б. Гермейера [84], Н.С. Кукушкина–В.В. Морозова [137], Э. Мулена [158]. В частности, в работе [84] для игр в нормальной форме на основе субъективного и объективного описания обстановки игры (см. стр. 2–3 реферата [84] и сноску в п.1.2) и понятия стратегий с информационным, смешанным расширением с использованием побочных платежей и с учетом способов обмена информацией (см. стр. 3–6 реферата [84]) приводится детальный анализ принципов оптимальности (принципов выбора рациональных стратегий). При этом учитываются информационные условия, степень коллективности действий и потребности практики (см. стр. 8–14 реферата работы [84]): оптимизация критерия коалиции-кооперации; оптимизация с осреднением; принцип максимина с позиции оперирующей стороны; принцип максимина в сочетании с коалиционной оптимизацией и оптимизацией с осреднением; получение абсолютно-оптимальной стратегии; получение стратегии наказания и поощрения; принцип гарантированного результата при обмене информацией в многошаговых играх с фиксированной последовательностью принимаемых решений; строгое и нестрогое (не единственность) равновесие и его связь с максимином, абсолютно-оптимальными стратегиями. Сделаны выводы о более общих свойствах равновесия, чем решения в БДИ. Приведен подробный анализ преимуществ и недостатков коалиций и методов их организации (см. стр. 15–22 реферата [84]). Далее приводится краткий библиографический перечень некоторых классических и современных направлений. В рамках методов исследования гарантированных решений (максиминных и минимаксных задач) наиболее известны следующие конструктивные направления (полностью см. [54]: обзоры глав 7, 8 по антагонистическим играм). Это направления: Н.Н. Красовского–А.И. Субботина–А.Г. Ченцова–В.Д. Батухтина, В.М. Кейна, а также Е.А. Ивановой–Е.М. Воронова–А.В. Савина, например [15, 76, 111, 118, 129, 130, 245] [см. обзор гл. 7], на основе принципа экстремального направления областей достижимости; Р. Айзекса–Р. Беллмана–Ж.М. Андерсона, Д. Блекуэлла [см. обзор гл. 7] на основе динамического программирования и анализа сингулярностей нелинейных задач управления; В.Ф. Демьянова–В.Н. Малоземова–В.В. Федорова [94, 250], связанного с н/д условиями минимакса и максимина с аналитическими и численными методами определения решений; Л.С. Понтрягина–А.М. Летова–А.М. Баткова–Д.С. Иргера–В.М. Александрова–А.Д. Шараборова, а также Е.М. Воронова–В.А. Карабанова–А.П. Карпенко–А.П. Маслова [209, 210] [см. также обзор главы 8] и [3, 26, 27, 61–66] на основе детерминированного и стохастического принципа максимума или комбинации принципа максимума и фильтрации; А.Б. Куржанского [140] на основе методов наблюдения и управления ансамблем траекторий; Л.А. Петросяна–О.А. Малафеева–Г.В. Томского [см. обзор главы 7] и [199] на основе непрерывно-дискретных динамических игр; Ф.П. Черноусько, А.А. Меликяна [257], посвященное исследованию задач управления и поиска с перерывом поступления информации, эллипсоидными оценками и применением областей достижимости и неопределенности; А.Н. Лысенко, например [98], на основе аналитического конструирования и линейного наблюдения; Ю.Б. Гермейера [83] с глубоким анализом информационно-тактических свойств гарантирующих решений в исследовании операций; А. Брайсона, М. Берковица, У. Флеминга [278] на основе вариационных подходов; В. Явина – стохастическое преследование и уклонение [420] и др. В [54] проведен подробный анализ неантагонистических игр.В рамках подходов на основе коалиционного равновесия: обзор по Нэш-оптимизации дан в главе 2, обзор по векторным равновесиям, коалиционному равновесию и V-решениям дан в главах 3,4. Обзор по методам векторной оптимизации дан в главе 3, анализ кооперативной игры на основе характеристической функции дан в главе 5. Развернутый обзор по существующим подходам на основе СТЭК дан в главе 6. Кроме ряда фундаментальных и обзорных работ по неантагонистическим играм, например, Э.М. Вайсборда–В.Н. Жуковского [32], Э.Й. Вилкаса [39], Ю.Б. Гермейера [84], Н.С. Кукушкина–В.В. Морозова [137], Э. Мулена [168], следует отметить следующих авторов, чьи результаты внесли вклад в развитие неантагонистических игр и анализ работ которых дан в обзорах [54]: В.Ф. Бирюков, В.И. Борисов, Н.Н. Воробьев, В.М. Гаврилов, Ю.Б. Гермейер, В.В. Гороховик, А.Н. Джафаров, В.В. Дружинин, Г.И. Дюбин, В.Ю. Зверев, Ю.М. Ермольев, А.П. Карпенко, А.Ф. Кононенко, В.Ф. Крапивин, В.В. Кротов, А.Б. Куржанский, О.И. Ларичев, Ц.Г. Литовченко, Р. Льюс, Л.Н. Лысенко, Н.Н. Моисеев, А.А. Меликян, О. Моргенштерн, Д. Нейман, В.Д. Ногин, В.Н. Опойцев, Г. Оуэн, Р.А. Поляк, В.П. Пацюков, Л.А. Петросян, В.В. Подиновский, М.Е. Примак, Л.С. Понтрягин, Х. Райфа, Л.А. Растригин, Т. Саати, М.Е. Салуквадзе, В.А. Серов, Э.Р. Смольяков, Е.В.Смирнова, И.М. Соболь, Р.Б. Статников, В.Г. Суздаль, Г.В. Томский, А.Л. Топчишвили, Н.Т. Тынянский, М.М. Хрусталев, Ф.Л. Черноусько, S.L. Anderson, T.Basar, L.D. Berkovitz, I.H. Case, E.L. Dockher, I.V. Friedman, D. Ghose, I.C. Harsanyi, A. Haurie, S. Jorgensen, G. Leitman, M. Margiacco, H. Mukai, J. Nash, V. Pareto, L.F. Pau, B. Petrovic, V.R. Prasad, A. Ray, J.K. Sengupta, L.S. Shapley, R.Selten, H.L. Stalford, A.W. Starr, D. Yeung, J. Yong, P. Yu, L.S. Zazemba и др. Следует отметить, что распределение принципов оптимальности по элементу классификации игр на игры с противоположными и непротивоположными интересами (неантагонистические игры) является условным, так как, к примеру, минимаксные (или максиминные) подходы могут быть применены и в играх с непротивоположными интересами при недостатке информации о партнерах, при формировании характеристической функции и арбитражной схемы. Более того, в цитированной работе [84] ряд постановок и условий для игр с непротивоположными интересами сформированы на основе обобщенного автором принципа гарантированного результата. В качестве второго примера «перемешивания» принципов конфликтного взаимодействия является условность их отношения к стратегическим и нестратегическим (кооперативным) играм. Так, из определения 1.9 следует, что единая коалиция действия кооперации порождает единую стратегию, которая совпадает с ситуацией, в отличие от определения 1.3. Понятие стратегии теряет смысл [190, стр. 17], и принятие решения в кооперативной игре принимает вид нормативного договорного акта (обязательного соглашения [168]). Результатом соглашения становится совместное получение «справедливого» дележа. Но подобный результат может быть получен после создания коалиции-кооперации, а в процессе ее организации решаются задачи стратегического характера. Во-первых, необходимо создать механизм обеспечения устойчивости коалиции-кооперации при неудовлетворенности участников кооперации результатами дележа и, во-вторых, обеспечить наилучшие для всех объектов условия дележа введением «арбитражной» [84] характеристической функции объекта (определение 1.8). Более детально вопрос образования коалиций-коопераций, как одной из основ компромиссов, рассмотрен в обзоре главы шесть, но уже здесь имеет смысл упомянуть, что, например, в фундаментальной работе [84] обсуждаются три степени коллективности действий (см. стр. 6 реферата [84]) и три формы объединения в коалицию с повышением степени коллективности (см. стр. 7–8 реферата [84]), анализируются (см. стр. 15–22 реферата [84]) девять условий образования коалиции, три условия невозможности коалиции, обсуждаются шесть трудностей их организации, причем часть трудностей преодолевается применением формализации (определение 1.8) и введением понятия игры с повторением, на базе которой формируется условие устойчивости кооперативного решения в коалиции. Конструктивны в этом направлении и результаты работы [137]. Отмечается, что принципы конфликтного взаимодействия, принципы кооперативной оптимальности, элементы классификации взаимосвязаны в рамках практической задачи и эти взаимосвязи порождают различные формы компромисса. Можно выделить ряд свойств задач управления ММС, которые свидетельствуют о необходимости формирования компромиссов и создают определенную основу для этого: · наличие в целевой эффективности ММС индивидуальных и общих интересов; · изменение информационных условий в ММС (неполнота информации и информационное «перемирие» с добровольным обменом (при наличии искажений – «блефа») и «добыванием» информации, связь субъективной и объективной информационных ситуаций); · возможности и условия образования коалиций и различных коалиционных структур в ММС для повышения индивидуальной и общей эффективности в ММС на основе предостережения (наказания и поощрения); · комбинации стабильных и эффективных решений на основе необязательных соглашений или обязательной договорной основе (например, выбор наиболее эффективного стабильного решения, стабильного среди эффективных и др.); · стремление ММС к предельному целевому качеству с обеспечением минимальной межуровневой конфликтности (между «арбитром» и «линейкой» равнозначных объектов – коалиций ММС) на основе обобщенного гомеостаза и т.д. Как указано выше, эти и другие вопросы детально обсуждаются и развиваются в главе шесть и в [54]. 1.5. Основные определения эффективности и стабильности. Целью данной работы является изучение методов и алгоритмов стабильного и эффективного управления, способов формирования стабильно-эффективных компромиссов ММС (СТЭК ММС) с последующим применением средств автоматизированного проектирования и реализацией методов в прикладных задачах. Определения стабильности и эффективности, используемые в работе, без ограничения общности сформулируем в рамках параметризованных управлений и/или процедур принятия решения, причем на общий вектор параметров где Понятия эффективного управления базируется на Парето-оптимальном решении, Определение 1.11.Пусть множество индексов коалиции Определение 1.12.Пусть Пусть
Рис. 1.3. Парето- и На рис. 1.3 для Из рис. 1.3 видно, что прямоугольный конус типа конуса с вершиной в точке С1 удовлетворяет всей области П-Парето-решений, а «узкий» конус с вершиной С2 выделяет на Парето-области подобласть Определение 1.13.Набор параметров где Стабильные решения формируются в виде гарантирующих решений, скалярного равновесия по Нэшу, векторных равновесий (векторное равновесие по Нэшу, Определение 1.14.Набор решений где Определение 1.15(частный случай определения 1.14). Если
Определение 1.16.Набор параметров Определение 1.17. Набор векторов параметров на множестве P допустимых коалиционных структур существует возможность создания контркоалиции Определение 1.18.Набор параметров Определение 1.19. Набор векторов параметров Определения стабильных и эффективных решений позволили далее описать методы поиска этих решений на основе математического и алгоритмического обеспечения (см. главы 2–5, 7, 8 данного исследования и работу [54]). На рис. 1.4а представлены восемь основных методов и алгоритмов. Данные методы и алгоритмы были реализованы в рамках разработанных программных систем (глава 9): · ПС «МОМДИС» (многокритериальной оптимизации многообъектных динамических систем с разработкой методов и алгоритмов определения Нэш, Парето, УКУ, Шепли и др. решений) в программной среде «MATLAB»; · ПС «FILTR» (оптимизация стохастических антагонистических моделей в интегро-дифференциальной форме) на основе фильтрации и управления); · ПС «ГАРАНТИЯ-М» (программная реализация программно-корректи-руемого закона управления на основе экстремального прицеливания) в программной среде DELPHI; · ПС в «MATLAB» (проработка алгоритмов поиска векторного равновесия). На рис. 1.4а справа указана степень проработки каждого алгоритма в соответствии с рис. 1.4б.
Рис. 1.4а. Применяемые методы и алгоритмы взаимодействия объектов и коалиций
Рис. 1.4б. Схема, иллюстрирующая уровень проработки алгоритма
Рис. 1.4в. Классификация СТЭК Для ряда алгоритмов были исследованы возможности их параллельной реализации (см. главу 9). На рис. 1.4в дана классификация стабильно-эффективных компромиссов (СТЭК) ММС на основе необязательных соглашений Мулена и строгой договорной основе (см. главу 6). Рис. 1.5 иллюстрирует смысл компромиссов на основе комбинации Парето–Нэш–УКУ–Шепли-подходов.
Рис. 1.5. Компромиссы на основе комбинации Парето-Нэш-УКУ-Шепли-подходов: СТЭКи заключаются в выборе недоминируемого наиболее эффективного Нэш-решения (точка Н), формировании Парето–Нэш-области компромиссов (ПНОК) на основе прямоугольного конуса СНД, границей которой является Парето-граница. В области ПНОК выбираются УКУ-решения в той или иной степени близости к точке Шепли либо к «идеальной» точке. Участникам игры имеет смысл выполнять необязательные соглашения в связи с устойчивостью ситуации в точке УКУ-решения. В рамках обязательных соглашений рассматриваются комбинации арбитражных схем с УКУ–Нэш-равновесием, среднеквадратических решений с точкой Шепли и др. (см. гл. 6). Игровые подходы имеют большую значимость в развитии интеллектуальных систем управления (ИСУ) [215], в состав которых входят, по меньшей мере, два присущих лишь ИСУ блока: динамическая экспертная система (ДЭС) и подсистема предельного целевого качества (ППЦК). Кроме необходимости пополнения базы знаний ДЭС разрабатываемыми игровыми алгоритмами, с одной стороны, и интеллектуализации компромиссов с учетом возможностей ИСУ, с другой стороны, в настоящее время разрабатывается концепция формирования ППЦК на основе игровых компромиссов в ММС и обобщенного гомеостаза [46, 216, 412] (см. гл. 6, 12), а также на основе игровых компромиссов в иерархических системах [218]. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 357. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
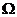 -равновесия и др.), коалиционного равновесия на основе
-равновесия и др.), коалиционного равновесия на основе  -оптимизация, дележ по Шепли, среднеквадратическая стратегия, арбитражная схема и др.).
-оптимизация, дележ по Шепли, среднеквадратическая стратегия, арбитражная схема и др.).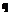 наложены ограничения
наложены ограничения  , где
, где ,
, .
.

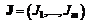 . Вектор
. Вектор 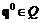 оптимален по Парето, если из условия
оптимален по Парето, если из условия  следует либо
следует либо  , либо система неравенств несовместна и хотя бы одно из неравенств противоположного смысла.
, либо система неравенств несовместна и хотя бы одно из неравенств противоположного смысла. .
. – новый векторный показатель вида
– новый векторный показатель вида  . Тогда оптимальное по Парето множество для
. Тогда оптимальное по Парето множество для  совпадает с
совпадает с  .
.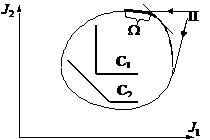
 -оптимальность
-оптимальность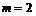 приведены два конуса
приведены два конуса 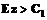 и
и  .
.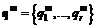 называется оптимальным по Шепли, если обеспечивает
называется оптимальным по Шепли, если обеспечивает  , где
, где  – функция Шепли, которая, например, при
– функция Шепли, которая, например, при 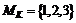 имеет вид [152]
имеет вид [152]
 – характеристическая функция, как точка равновесия по Нэшу (см. определение 1.14). Например,
– характеристическая функция, как точка равновесия по Нэшу (см. определение 1.14). Например,  означает:
означает:  ,
,  ,
, 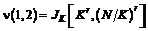 .
. является равновесным по Нэшу относительно скалярного показателя
является равновесным по Нэшу относительно скалярного показателя  , который является функцией эффективности коалиции
, который является функцией эффективности коалиции  , если для любого
, если для любого ,
,  ,
,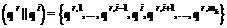 .
. и цели антагонистические, т.е.
и цели антагонистические, т.е. 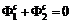 , то равновесие по Нэшу превращается в седловую точку
, то равновесие по Нэшу превращается в седловую точку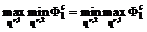 .
. называется гарантирующим решением для показателя
называется гарантирующим решением для показателя  коалиции
коалиции 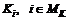 , если
, если 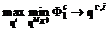 .
.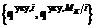 , где
, где  называется коалиционным равновесием (V-решением в форме угроз-контругроз (УКУ)) при показателе коалиции
называется коалиционным равновесием (V-решением в форме угроз-контругроз (УКУ)) при показателе коалиции  , если при попытке коалиции
, если при попытке коалиции 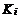 улучшить свой показатель (угроза –
улучшить свой показатель (угроза – 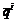 )
)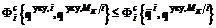
 , для которой реализуется контругроза
, для которой реализуется контругроза 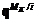
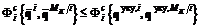 ;
; .
. 
 является равновесным по Нэш относительно векторного показателя
является равновесным по Нэш относительно векторного показателя  , где
, где 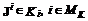 (фиксированная коалиционная структура), если набор
(фиксированная коалиционная структура), если набор  и
и  из условия
из условия  следует лишь
следует лишь 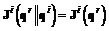 (т.е. на векторе
(т.е. на векторе  имеет место Парето-оптимальность).
имеет место Парето-оптимальность). называется W-равновесным относительно векторного показателя
называется W-равновесным относительно векторного показателя  , где
, где  , если
, если  и
и  из условия
из условия  , где
, где  , следует либо
, следует либо  , либо его несовместность (т.е. на векторе
, либо его несовместность (т.е. на векторе 


