
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Общее определение игры. Частные классы игрДостаточное общее определение игры дано в работах Э.Й. Вилкаса [39] и Н.Н. Воробьева [43] (см., например, реферат работы [39] в приложении к работе1). Определение 1.1 [26]. Игрой называетсянабор где N – произвольное множество игроков, Индивидуальные предпочтения, как правило, формируются на некоторых отображениях Множество Определение 1.2. Коалиционной структурой (разбиение множества N) называется такое семейство коалиций Если игроки разбились на коалиции и эти коалиции выбрали свои стратегии, то считается, что игра Г разыграна. Определение 1.3. Для любой коалиционной структуры P набор стратегий При реализации ситуации  Замечание 1.1. При отсутствии коалиций
Более полное представление об игровых структурах дают следующие два обобщения определения 1.1: 1) Могут иметь место пересекающиеся коалиции. Тогда пункт два определения 1.2 выполняется, например, для всех 2) С учетом определения игры по Н.Н. Воробьеву [43], когда действия и интересы представляются в разных коалиционных структурах Определение 1.4. Игрой с разными наборами коалиций действия и интересов называется набор с реализацией Кроме исхода игры, вводится понятие состояния игры и множества стратегий ставятся в зависимость от состояния игры. Определение 1.5[39]. Динамической игрой называется набор где Реализация динамической игры состоит из последовательности состояний игры Данная формулировка [39] расширяет обычное понятие динамической игры. В обычных динамических играх – основная проблема в обмене информацией между участниками игры, а коалиции образуются по предписанным правилам или до начала игры. Обычная динамическая игра в нормальной форме соответствует одному шагу игры в определении 1.5. В рамках определения 1.1 можно сформировать, как частные случаи, определения бескоалиционных, коалиционных и кооперативных игр. Так, если зафиксировать во множестве коалиционных структур
Определение 1.6.Бескоалиционной игрой при фиксированном Р называется набор где Р – фиксированное разбиение, Аналогичное описание коалиционной игры приводит к следующему определению. Определение 1.7. Коалиционной игрой называется набор
Для получения определения кооперативной игры вводится характеристическая функция Определение 1.8. Кооперативная игра на основе характеристической функции где
Частный случай кооперативной игры может быть сформулирован на основе векторной оптимизации. Определение 1.9 [32]. Кооперативной игрой называется набор где И, наконец, в плане иерархических игр один или несколько игроков ограничивают множество исходов остальных за счет права первого хода. Остальные игроки в зависимости от условий разыгрывают игру в рамках одного из четырех классов игр. В работе Э.Н. Вайсборда, В.И. Жуковского [32] предложено следующее определение. Определение 1.10 [32]. Иерархической игрой называется набор где N – число игроков в игре, L – число игроков, имеющих право первого хода, |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 379. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,
,  (1.1)
(1.1)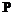 – множество коалиционных структур
– множество коалиционных структур  , K – коалиция – группа игроков, которой приписаны действия и интересы,
, K – коалиция – группа игроков, которой приписаны действия и интересы,  – произвольное множество стратегий коалиции
– произвольное множество стратегий коалиции  (при любом Р:
(при любом Р: 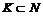 ); S – произвольное множество всех исходов игры на
); S – произвольное множество всех исходов игры на 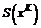 – множество возможных исходов на
– множество возможных исходов на  ,
,  — транзитивное отношение предпочтения коалиции
— транзитивное отношение предпочтения коалиции 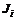 из
из 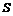 , которые являются функциями выигрыша (потерь). Тогда предпочтительность исхода
, которые являются функциями выигрыша (потерь). Тогда предпочтительность исхода  по сравнению с исходом
по сравнению с исходом  (
(  ) означает, что
) означает, что  для всех
для всех  .
. позволяет каждой коалиции оценивать, как выбор коалицией K конкретной стратегии
позволяет каждой коалиции оценивать, как выбор коалицией K конкретной стратегии  изменяет множество возможных исходов.
изменяет множество возможных исходов.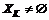 для всех
для всех  (и
(и 
 для всех K,
для всех K,  , (1.2)
, (1.2) для любого
для любого  .
. называется ситуацией в игре.
называется ситуацией в игре. множество исходов сужается до
множество исходов сужается до 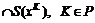 . Далее предполагается, что последнее множество исходов состоит из единственного элемента [39].
. Далее предполагается, что последнее множество исходов состоит из единственного элемента [39].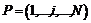 ,
,  получаем частный случай определения 1.1
получаем частный случай определения 1.1 .
.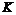 и
и  , кроме некоторых `
, кроме некоторых `  . Если две пересекающиеся коалиции `
. Если две пересекающиеся коалиции `  и `
и ` 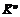 выбирают стратегии одновременно, то они должны обменяться информацией для согласования своего выбора, т.е. они действуют как коалиция`
выбирают стратегии одновременно, то они должны обменяться информацией для согласования своего выбора, т.е. они действуют как коалиция`  . Следовательно, для таких коалиций необходимо задавать
. Следовательно, для таких коалиций необходимо задавать  , из которого осуществляется одновременный выбор стратегий коалициями
, из которого осуществляется одновременный выбор стратегий коалициями  и
и  соответственно, причем
соответственно, причем  ,
,  , ситуация
, ситуация  порождает исход
порождает исход  , отношения предпочтения формируются над коалициями
, отношения предпочтения формируются над коалициями  , а исходное определение 1.1 игры принимает вид следующего определения.
, а исходное определение 1.1 игры принимает вид следующего определения. (1.3)
(1.3) ,
,  , (1.4)
, (1.4) ,
, 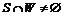 – произвольные множества игроков, коалиционных структур, неокончательных состояний игры и множества окончательных исходов игры;
– произвольные множества игроков, коалиционных структур, неокончательных состояний игры и множества окончательных исходов игры;  – произвольное множество стратегий коалиции
– произвольное множество стратегий коалиции  ;
;  – множество исходов (как окончательных, так и неокончательных) после применения коалицией стратегий
– множество исходов (как окончательных, так и неокончательных) после применения коалицией стратегий  ;
;  и коалиционных структур
и коалиционных структур  в данных состояниях и выбранных ситуаций
в данных состояниях и выбранных ситуаций  ,
, 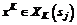
 , причем в ситуациях
, причем в ситуациях  возможны исходы из S, в том числе
возможны исходы из S, в том числе 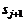 , а в ситуации
, а в ситуации 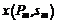 – только из W. То есть из
– только из W. То есть из  следует
следует 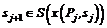 ,
,  ,
,  .
. ), то на фиксированной структуре
), то на фиксированной структуре  (на N) коалиции (игроки) независимо друг от друга выбирают свои стратегии
(на N) коалиции (игроки) независимо друг от друга выбирают свои стратегии 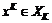 ,
,  . Пусть предпочтения коалиций (игроков) представлены их функциями выигрыша
. Пусть предпочтения коалиций (игроков) представлены их функциями выигрыша  на множестве ситуаций
на множестве ситуаций  . Ситуации становятся исходами игры. Выбор стратегии `
. Ситуации становятся исходами игры. Выбор стратегии `  коалицией K (игроком i) ограничивает множество исходов до множества стратегий
коалицией K (игроком i) ограничивает множество исходов до множества стратегий .
. , (1.5)
, (1.5) или
или 
 , при отсутствии разбиения Р¹ Æ – набор
, при отсутствии разбиения Р¹ Æ – набор . (1.6)
. (1.6) , (1.7)
, (1.7) (при любом множестве Р
(при любом множестве Р  .
. ,
,  всех подмножеств множества игроков N,
всех подмножеств множества игроков N,  .
. согласно силе коалиции
согласно силе коалиции  , (1.8)
, (1.8) ;
;  ;
;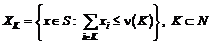 ;
;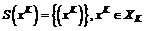 ;
;  означает
означает 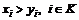 .
.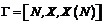 , (1.9)
, (1.9) – множество ситуаций.
– множество ситуаций. , (1.10)
, (1.10)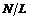 – число координируемых игроков,
– число координируемых игроков,  – общее множество стратегий,
– общее множество стратегий,  – множество стратегий координируемых игроков.
– множество стратегий координируемых игроков.