
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Математическая модель конфликтной ситуации в ММСВ соответствии с определениями игры математическая модель конфликтной ситуации должна содержать четыре компоненты: математическая модель ММС с выбором описания и управляющих сил, векторный целевой показатель, характер коалиционных объединений и принцип конфликтного взаимодействия на основе стабильности и эффективности. Далее последовательно раскрывается модель конфликтной ситуации в форме дифференциальной игры в нормальной форме, когда выбор стратегий связан с выбором управлений, которые однозначно определяют исход в виде значения вектора показателей игры. 1.3.1. Математическая модель ММС с выбором описания Математическое описание ММС.В качестве основного описания ММС принимается система динамико-алгебраических связей где N – число объектов в ММС; Выражения (1.11) характеризуют динамические связи (а), алгебраические связи (б), вектор выхода (в) и функцию принятия решения и управления (г). Управление Свойства правых частей (1.11а), (1.11б) типичные (см., например, реферат работы [32] в приложении к1), в основном, это непрерывность и дифференцируемость, а для (1.11а) – выполнение условий Липшица.  О выборе управляющих сил.Как известно, существуют три основных способа задания управляющих сил: 1) Вектор параметров 2) Программное управление 3) Закон управления (или позиционное управление) Свойства управлений и множеств управлений варьируются, но типичные свойства можно найти, например в [32] (см. реферат [32] в приложении к1). Наиболее желаемые свойства U – это свойства выпуклости и компактности (или слабой компактности) [121]. Ввиду сложности краевых задач в ММС имеет смысл ориентироваться на комбинацию приближенных гибких вычислительных схем и классических оптимизационных структур управления, например, математического программирования и оперативного управления [203], с существенной параметризацией управляющих сил во временных интервалах их приложения. Поэтому, кроме трех указанных, рассматриваются следующие комбинации в представлении управляющих сил. 4) Параметризированное векторное программное управление где при этом Возможны обобщения (1.13а), (1.13б). Так, например, функции где Если управление (1.13а) непрерывное, то управление (1.13б) кусочно-непрерывное. Типичный частный вид последнего при fj(t) = 1 на 5) Параметризованный закон управления (стратегия) где 6) Программно-корректируемый закон управления (ПКЗУ) (стратегия) при заданном разбиении отрезка где на отрезке Замечание 1.2.Данный ПКЗУ отличается от кусочно-программной стратегии Л.А. Петросяна [199] где 7) Параметризованный ПКЗУ, который получается на основе комбинации 4 и 6, например, в виде (1.16), где с разбиением При параметризации управления и дискретизации временного интервала Во-первых, в точной задаче рассматривается, как правило, класс управлений с конечным числом точек разрыва первого рода, к которым принадлежат и аппроксимированные управления. Во-вторых, существенным является свойство сжатия функциональной связи показателей с управляющими силами, когда ограниченным структурным изменениям управляющих сил соответствует малое изменение значений показателей. Данное свойство грубости часто имеет место в задачах управления. В-третьих, очевидно, что при сведении исходной задачи к конечномерной задаче нелинейного программирования результат уточняется при определенном увеличении размерности вектора параметров. В этом случае контролируемые приближения для некоторых классов систем могут быть обеспечены, например, на основе спектральных методов развитых в работах В.В. Солодовникова, В.В. Семенова, А.Н. Дмитриева, Н.Д. Егупова и других [см., например, работу А.И. Трофимова, Н.Д. Егупова, А.Н. Дмитриева. Методы теории автоматического управления. – М.: Энергоатомиздат, 1997. – 654 с.]. Следует также отметить, что параметризация управляющих сил позволяет на основе параметрических сетей, например [238], преодолевать возрастающие трудности глобальной оптимизации в многокритериальных задачах, приближенно оценивать существование и единственность решения и назначать начальное приближение для локального поиска точного решения. В этом случае методы и алгоритмы приобретают, по меньшей мере, двухэтапную структуру. На первом этапе на основе сетевых подходов оценивается множество решений и выбирается начальное приближение в «выгодной» локальной области. На втором этапе на основе начального приближения решается точная задача определения параметризованного оптимального управления или управления в форме 2,3. 1.3.2. Векторный целевой показатель Целевые свойства ММС характеризуются вектором который представляет собой сложную функциональную связь с указанными величинами. Типичным видом i-й функции выигрыша (потерь) является функционал на Свойства (1.19) даны в приложении к работе1 (см. реферат работы [32], стр. 4). Кроме непрерывности (1.19) по (x, u) и дифференцируемости по управлению, желаемыми свойствами являются вогнутость-квазивогнутость (выпуклость-квазивыпуклость) функционала (1.19) на множестве управлений. При общих свойствах целевого вектора проблема глобальной оптимизации может быть преодолена, как отмечалось в п. 1.3.1, на основе двухэтапной структуры методов оптимизации с сетевым глобальным анализом и приближенным решением на первом этапе и точным локальным решением на втором. Несовпадение размерности J с числом объектов означает, что некоторые объекты имеют векторную цель. Размерность показателя будет совпадать с числом объектов в ММС, если показатель каждого объекта скаляризуется. 1.3.3. Коалиционная структура действий и интересов ММС Пусть Тогда где r есть, например, размерность множества индексов вектора параметров (после параметризации управлений) или множества индексов управлений (без параметризации); где m – размерность множества индексов вектора показателей. В свою очередь, каждой Далее ограничиваемся Тогда разбиение где R – множество индексов, например, управлений, М – множество индексов вектора показателей. Показатель каждой коалиции принимает, как правило, один из двух видов: причем сумма индексов Коалиционные управления без параметризации принимают вид выражения (1.11а) преобразуются к виду × Показатель в варианте (1.23б) где В рамках введенной модели конфликта обозначения в определении 1.1 имеют следующие соответствия: · множество стратегий · множество исходов-состояний · множество возможных исходов-состояний · предпочтения коалиции 1.3.4. Принципы конфликтного взаимодействия. В общем случае имеют место пять принципов конфликтного взаимодействия: · антагонизм · бескоалиционное взаимодействие; · коалиционное взаимодействие; · кооперативное взаимодействие; · иерархическое взаимодействие (с правом первого хода). Так как ММС, по определению, является системой равнозначных объектов (горизонтальный набор на рис. 1.1), то задачи с правом первого хода в данной работе не рассматриваются. Уже данное перечисление показывает, что свойства конфликтных взаимодействий робастны, так как позволяют делать здравые оценки эффективности в условиях неопределенности среды, неопределенности «активного партнера» и неопределенности цели с учетом характера неопределенности и конфликтности. Как известно, в данных принципах конфликтного взаимодействия заложены три фундаментальных понятия теории игр: стабильность, эффективность и стабильно-эффективный компромисс. Стабильность ММС – это обеспечение устойчивых (уравновешенных по целям) процессов функционирования и проектирования многообъектных структур в условиях конфликтности (несогласованности) и/или неопределенности. Эффективность ММС – это достижение максимального целевого качества объектов, коалиций и ММС в целом на основе устойчивого и рационального коалицианирования. По меткому замечанию Ю.Б. Гермейера [83, 84]: «Классическая теория игр в части теории принятия решений преждевременно и чрезмерно заформализована». Данный недостаток сказывается во многих приложениях, в которых, как правило, требуется комбинирование указанных принципов взаимодействия, что в свою очередь требует преодоления информационно-тактических несостыковок данных подходов. Поэтому вопросы формирования компромиссов еще полностью не сняты.
Рис. 1.2. Частная классификация дифференциальных игр Cтабильно-эффективный компромисс в ММС (СТЭК ММС) – это объединение стабильности и эффективности в рамках множества решений – от полного совпадения данных свойств в одной точке пространства J(или U) до обеспечения возможной степени сближения в условиях информационно-тактических расширений соглашений. СТЭК ММС дополняют СТЭК в иерархических системах (СТЭК ИС), где реализуется право первого хода на основе субъективной информации, что составляет тему отдельного исследования. Частная классификация дифференциальных игр с выделением учитываемых в работе свойств, которая обобщает модель конфликтной ситуации, дана на рис. 1.2, где АДИ, БДИ и т.д. – вид взаимодействия в дифференцированной игре (ДИ). Стохастические условия учтены в одном из классов АДИ (гл. 8). |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 378. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (1.11)
(1.11)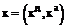 – вектор состояния ММС с
– вектор состояния ММС с  – динамическими и
– динамическими и  – алгебраическими состояниями;
– алгебраическими состояниями;  – множество состояний; y – вектор выхода ММС;
– множество состояний; y – вектор выхода ММС;  – вектор управления ММС;
– вектор управления ММС;  – вектор параметров ММС, которые характеризуют параметрическую неопределенность в (1.11а–в) и возможную параметризацию в (1.11г).
– вектор параметров ММС, которые характеризуют параметрическую неопределенность в (1.11а–в) и возможную параметризацию в (1.11г). , (1.12)
, (1.12)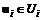 – подвектор управления i-м объектом ММС.
– подвектор управления i-м объектом ММС.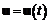 ;
; ,
,  , где
, где

 :
:  ,
,  ;
; 
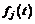 – непрерывные функции, заданные на отрезке
– непрерывные функции, заданные на отрезке  (1.13а) или на отрезке
(1.13а) или на отрезке  (1.13б);
(1.13б);  – интервал применения слагаемого управления
– интервал применения слагаемого управления 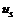 (1.13б)
(1.13б)
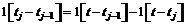 и
и  – заданное разбиение отрезка
– заданное разбиение отрезка  . Для сохранения числа l интервалов параметризации (1.13б) на каждом отрезке [tj-1,T] достаточно (1.13б) представить в виде
. Для сохранения числа l интервалов параметризации (1.13б) на каждом отрезке [tj-1,T] достаточно (1.13б) представить в виде (1.13в)
(1.13в) .
. . (1.14)
. (1.14)

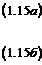
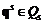 ,
,  – заданные непрерывные функции.
– заданные непрерывные функции.
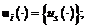
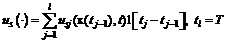 , (1.16)
, (1.16) – допустимое программное управление
– допустимое программное управление 
 и реализуемое на
и реализуемое на 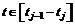 .
.
 – программное управление на
– программное управление на  при фиксированном значении
при фиксированном значении 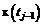 .
. (1.17)
(1.17) на отрезке
на отрезке 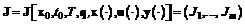 , (1.18)
, (1.18)
 . (1.19)
. (1.19) – коалиционная структура действий и интересов с размерностью
– коалиционная структура действий и интересов с размерностью 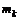 множества
множества  индексов коалиций в каждой, где
индексов коалиций в каждой, где  .
. , (1.20)
, (1.20) , (1.21)
, (1.21)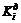 соответствует, например, при полной параметризации вектор параметров
соответствует, например, при полной параметризации вектор параметров 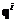 (или вектор
(или вектор 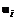 без параметризации). Каждой
без параметризации). Каждой  соответствует целевой вектор
соответствует целевой вектор  .
. .
. , (1.22)
, (1.22) ; (1.23а)
; (1.23а) ,
, 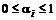 ,
,  , (1.23б)
, (1.23б) равна m.
равна m.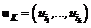 ,
,  , (1.24)
, (1.24)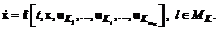 (1.25)
(1.25)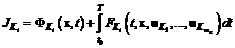 , (1.26)
, (1.26) ;
;  .
. множество
множество 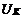 ;
;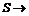 множество траекторий
множество траекторий  на множестве ситуаций
на множестве ситуаций 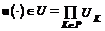 , или отображение Х, U на множество показателей
, или отображение Х, U на множество показателей  ;
; множество возможных траекторий вектора
множество возможных траекторий вектора  на множестве ситуаций
на множестве ситуаций  при фиксированном управлении
при фиксированном управлении 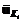 , где
, где  , или множество значений
, или множество значений  на множестве U;
на множестве U;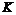 представлены максимизацией функции выигрыша (минимизацией потерь)
представлены максимизацией функции выигрыша (минимизацией потерь)  на множестве
на множестве 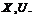
 ;
;