
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Каноническое уравнение эллипса.ОПР: Эллипсом называется геометрическое место точек, для каждой из которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами, есть данное число 2а, большее, чем расстояние между фокусами=2с ( F1, F2 – фокусы эллипса; расстояние между F1, F2, равное 2с – фокусное расстояние; а – большая полуось; О – середина F1F2 – центр эллипса, F1F2 – первая (фокальная) ось; прямая, проходящая через О ^ F1F2 – вторая ось. Теорема: Каноническое уравнение эллипса имеет вид
½F1M½+½F2M½³½F1F2½. При a=c, точка М принадлежит [F1,F2], при a>c , точка М не принадлежит [F1,F2]. Дан эллипс. Построим его каноническое уравнение. Введем систему координат. Начало возьмем совпадающее с центром эллипса, ось абсцисс направим по фокальной оси, ось ординат направим по второй оси. F1=(-с,0), F2=(с,0), М=(x,y) ½F1M½+½F2M½=2aÞ
Докажем, что если точка (х, у) удовлетворяет полученному уравнению, то она принадлежит эллипсу, то есть r1+r2=2a, где r1, r2 – фокальные радиусы. Из уравнения Получим Из уравнения Тогда ½a+ex½<a+ex. Аналогично ½a-ex½<a-ex. Тогда r1+r2= a+ex +a-ex =2a. ◄
Каноническое уравнение гиперболы. ОПР: Гиперболой называется геометрическое место точек, модуль разности расстояний каждой из которых до двух данных точек – есть положительное и постоянное число 2а. ½½F1M½-½F2M½½=2a, где M – любая точка гиперболы.  F1, F2 – фокусы гиперболы; расстояние между F1, F2, равное 2с – фокусное расстояние; а – большая полуось; О – середина F1F2 – центр гиперболы; F1F2 – первая (действительная) ось; прямая, проходящая через О ^ F1F2 – вторая (мнимая) ось. Эксцентриситет гиперболы
►½½F1M½-½F2M½½£½F1F2½. Дана гипербола. Построим ее каноническое уравнение. Введем систему координат. Начало возьмем совпадающее с центром гиперболы, ось абсцисс направим по фокальной оси, ось ординат направим по второй оси. Тогда F1=(-с,0), F2=(с,0), М=(x,y)
Докажем, что если точка (х, у) удовлетворяет полученному уравнению, то она принадлежит гиперболе, то есть r1+r2=2a, где r1, r2 – фокальные радиусы. Из уравнения Получим Из уравнения 1. x³0, тогда r1=а+ех, r2= -(а-ех), ½r1-r2½= 2a. 2. x<0, тогда r1= -а-ех, r2= а-ех, ½r1-r2½= 2a. ◄
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 278. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 - эксцентриситет эллипса). ½F1M½+½F2M½=2a, где M – любая точка эллипса.
- эксцентриситет эллипса). ½F1M½+½F2M½=2a, где M – любая точка эллипса.
 ► Из неравенства треугольника:
► Из неравенства треугольника: ,
,




 ,
, 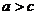 по определению
по определению 
 , b – малая полуось.
, b – малая полуось.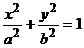 - каноническое уравнение эллипса.
- каноническое уравнение эллипса. .
. , и подставим значение y2 в r1.
, и подставим значение y2 в r1. .
. (так как 0<e<1).
(так как 0<e<1).
 Теорема: Каноническое уравнение гиперболы имеет вид:
Теорема: Каноническое уравнение гиперболы имеет вид: 
 Þ
Þ  ,
,


 ,
, 
 , b – малая полуось.
, b – малая полуось. получим
получим  , и подставим значение y2 в r1.
, и подставим значение y2 в r1. .
. .
.