
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теорема об общем уравнении плоскости в пространстве.Пусть в пространстве задана аффинная система координат. Уравнение Ax+By+Cz+D=0 (*) является уравнением плоскости тогда и только тогда, когда A, B, C – постоянные коэффициенты не равные нулю одновременно. ► Необходимость. Пусть (*) – уравнение некоторой плоскость
Пусть
Разкладывая определитель по элементам первой строки, получим
Следовательно, уравнение плоскости где Достаточность. Пусть (*) – уравнение первой степени. Для определенности будем считать, что
Так как уравнение (*) совпадает с уравнением плоскости Аналогично доказывается справедливость теоремы, если
Параметрическое уравнение плоскости: Выражая компланарность векторов В самом деле, из компланарности указанных векторов и неколлинеарности векторов Представляя полученное векторное равенство в координатах, получим параметрическое уравнение плоскости
t, u – действительные числа. Придавая различные значения для t и u, получим точки, принадлежащего плоскости  Нормальный вектор и теорема о расстоянии от точки до плоскости. Рассмотрим прямоугольную систему координат. ОПР: нормалью к плоскости называется перпендикулярный вектор, проведенный к плоскости из начала координат. Пусть в прямоугольной декартовой системе координат плоскость Любое уравнение Ax+By+Cz+D=0 плоскости
В самом деле
►Очевидно, что
Тогда С другой стороны имеем:
КРИВЫЕ ВТОРОГО ПОРЯДКА. Канонические ур-ия эллипса, гиперболы и параболы. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 275. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .Эту плоскость можно задать точкой
.Эту плоскость можно задать точкой  и направляющим подпространством
и направляющим подпространством  . Тогда имеем:
. Тогда имеем:
 Так как
Так как  , то
, то

 имеет вид: Ax+By+Cz+D=0,
имеет вид: Ax+By+Cz+D=0,
 . Зададим плоскость
. Зададим плоскость  и имела направляющими векторами вектор
и имела направляющими векторами вектор  и вектор
и вектор  Заметим, что координаты точки
Заметим, что координаты точки  удовлетворяют уравнению (*), а координаты векторов
удовлетворяют уравнению (*), а координаты векторов 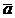 и
и  удовлетворяют уравнению Ax+By+Cz+D=0. По предыдущему пункту доказательства
удовлетворяют уравнению Ax+By+Cz+D=0. По предыдущему пункту доказательства 
 или
или  .◄
.◄ через параметры, получим параметрическое уравнение плоскости.
через параметры, получим параметрическое уравнение плоскости. , где t и u – однозначно определяемые числа (параметры т. М).
, где t и u – однозначно определяемые числа (параметры т. М).
 (1)
(1) Если в этом уравнении имеет место равенство
Если в этом уравнении имеет место равенство  , т.е.
, т.е.  , то уравнение называется нормальным уравнением плоскости.
, то уравнение называется нормальным уравнением плоскости.
 - нормально уравнение прямой плоскости
- нормально уравнение прямой плоскости 
 Теорема: Пусть плоскость
Теорема: Пусть плоскость  - произвольная точка. Тогда
- произвольная точка. Тогда 
 , где
, где  .
. - с одной стороны.
- с одной стороны. . Отсюда следует, что:
. Отсюда следует, что:  ◄
◄