
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
При решении задач без выводаЗакон Кулона (сила F взаимодействия двух точечных неподвижных зарядов Q1 и Q2)
где e - относительная диэлектрическая проницаемость среды; Линейная t и поверхностная s плотности заряда
Напряженность электрического поля: а) через величину пробного заряда q, внесенного в электрическое поле
где б) созданного точечным зарядом Q на расстоянии r от него
в) образованного бесконечной прямой равномерно заряженной нитью на расстоянии r от нее
где t - линейная плотность заряда на нити; г) образованного бесконечной равномерно заряженной плоскостью
где s - поверхностная плотность заряда; д) образованного разноименно заряженными параллельными бесконечными плоскостями (поле плоского конденсатора)
е) образованного заряженной сферой радиуса R
где r – расстояние от центра сферы Связь между напряженностью
Теорема Гаусса (поток ФЕ вектора напряженности электрического поля через замкнутую поверхность S, охватывающую точечные заряды Qi)
Потенциал электрического поля
где Wn – потенциальная энергия пробного заряда q, внесенного в это поле. Потенциал электрического поля, созданного точечным зарядом Q
Напряженность и потенциал поля, создаваемого проводящей заряженной сферой радиусом R на расстоянии r от центра сферы а) Е = 0, б) в) где Q – заряд сферы. Напряженность и потенциал поля, создаваемые системой точечных зарядов (принцип суперпозиции электрических полей): 
где Связь потенциала j с напряженностью а) б) в) Напряженность и потенциал электрического поля, создаваемого распределенными зарядами:
где Работа перемещения заряда q в электрическом поле
Энергия W взаимодействия системы точечных зарядов Q1, Q2, …, Qn
здесь ji – потенциал поля, создаваемого всеми (n-1) зарядами (за исключением i–ого), где расположен заряд Qi. Электрический момент диполя
где Электрическая емкость уединенного проводника и конденсатора:
где Q – заряд, сообщенный проводнику (пластине конденсатора); j - потенциал проводника; Электрическая емкость: а) уединенной проводящей сферы радиуса R
б) плоского конденсатора
где S – площадь одной пластины; d – расстояние между пластинами. Энергия уединенного заряженного проводника:
где C – емкость проводника; j - потенциал проводника (j¥ = 0). Энергия заряженного конденсатора
где U – разность потенциалов на обкладках конденсатора. Электроемкость системы конденсаторов: а) при параллельном соединении
б) при последовательном соединении
Сила и плотность электрического тока
где dQ – заряд, прошедший через конечное сечение проводника за время dt; dS – элемент площади поперечного сечения проводника. Сопротивление R и проводимость G проводника
где r -удельное сопротивление; l –длина проводника; g - удельная проводимость; S – площадь поперечного сечения. Сопротивление системы проводников: а) б) где Ri – сопротивление i – ого проводника. Закон Ома: а) б) в) Законы Кирхгофа: а) б) где Закон Джоуля – Ленца (количество теплоты Q, выделившееся на сопротивлении R за время t при прохождении через него электрического тока):
Полная мощность, развиваемая источником постоянного тока
Полезная мощность PR, выделяемая на внешнем сопротивлении R
КПД источника тока
Примеры решения задач Пример 1. Два точечных электрических заряда Q1 = 10 нКл и Q2= -20 нКл находятся в среде с диэлектрической проницаемостью ε = 2 на расстоянии d = 10 см друг от друга. Определить напряженность Е и потенциал j поля, создаваемого этими зарядами в точке А, удаленной от заряда Q1 на расстояние r1=10 см и от заряда Q2 на расстояние r2 =7 см.
Решение: Согласно принципу суперпозиции электрических полей, каждый заряд создает электрическое поле независимо от присутствия в пространстве других зарядов. Поэтому напряженность Модули напряженности электрических полей, создаваемых точечными зарядами Q1 и Q2 в среде с диэлектрической проницаемостью e рассчитываются по формулам: Вектор Модуль вектора где a -угол между векторами
В данном случае во избежание громоздких записей удобно значение cosa вычислить отдельно:
Подставляя выражение Е1 из уравнения (3.1) и Е2 из уравнения (3.2) в (3.3) и вынося общий множитель 1/(4pee0) за знак корня, получаем В соответствии с принципом суперпозиции электрических полей потенциал j результирующего поля, создаваемого двумя зарядами Q1 и Q2, равен алгебраической сумме потенциалов Потенциал электрического поля, создаваемого точечным зарядом Q на расстоянии r от него, выражается формулой В нашем случае согласно формулам (3.5) и (3.6) получим
Произведем проверку единиц измерения:
Произведем вычисления:
Ответ: Напряженность и потенциал в точке А соответственно равны Е = 5,6×104 В/м, j = -835 В. Пример 2. На тонком стержне длиной l = 40 см находится равномерно распределенный электрический заряд. На продолжении оси стержня на расстоянии а = 20 см от ближайшего конца находится точечный заряд Q1 = 4 нКл, который взаимодействует со стержнем с силой F = 10 мкН. Определить линейную плотность t заряда на стержне.

Решение: Выделим из стержня (рис. 3.2) малый участок dr с зарядом dQ =tdr, где t - линейная плотность заряда. Этот заряд можно рассматривать как точечный. Тогда, согласно закону Кулона для точечных зарядов в вакууме, сила взаимодействия
Интегрируя это выражение в пределах от а до a+l получим,
Откуда
Произведем проверку единиц измерения:
Произведем вычисления:
Ответ: Линейная плотность заряда на стержне t = 83,3×10-9 Кл/м = 83,3 нКл/м.
Решение: Работа A внешней силы по перемещению заряда q из точки поля с потенциалом j1 в другую точку с потенциалом j2 равна по абсолютной величине, но противоположна по знаку работе Работа сил электрического поля определяется по формуле
Тогда где j1 – потенциал в начальной точке; j2 – потенциал в конечной точке. Потенциал, создаваемый заряженным шаром радиусом R в точке на расстоянии r от его поверхности, определяется по формуле где Q = 4spR2 – заряд шара. Потенциал j1 в бесконечно удаленной точке (при r ® ¥) будет равна нулю. Воспользуемся выражением (3.8) для потенциала j2 и подставим в формулу (3.7); после преобразований получим
Проверим единицы измерения:
Расчет:
Ответ: Работа перемещения заряда из бесконечности в данную точку поля равна А = 2×10-4 Дж. Пример 4. Между пластинами плоского конденсатора, находящимися на расстоянии d0 = 1 см, приложена разность потенциалов U1 = 200 В. К одной из пластин конденсатора прилегает плоскопараллельная стеклянная пластина (e1 = 7) толщиной d1 = 9 мм. Конденсатор отключают от источника напряжения и после этого вынимают пластину. Определить разность потенциалов между пластинами конденсатора. Во сколько раз изменится энергия конденсатора?
Решение: Разность потенциалов между пластинами конденсатора в случае отключения его от источника напряжения находится из условия, что заряд на его пластинах остается неизменным, то есть где С1 и С2 – емкости конденсатора; U1 и U2 – разности потенциалов. В условиях данной задачи конденсатор вначале является слоистым и его емкость С1 находится по формуле, используемой для определения емкости батареи последовательно соединенных конденсаторов где S – площадь пластин; e1 и e2 – диэлектрические проницаемости стекла и воздуха; d1 – толщина стеклянной пластины; d0 – зазор между пластинами. После удаления стеклянной пластины из зазора конденсатор становится простейшим плоским конденсатором с емкостью Разность потенциалов U2, которая устанавливается после удаления из зазора стеклянной пластины, определим из формулы (3.9), подставляя в нее формулы (3.10) и (3.11) и производя соответствующие преобразования: Энергия заряженного конденсатора:
Изменение энергии конденсатора найдем, узнав отношение энергии конденсаторов: Это отношение можно определить двумя способами: 1. Если подставить выражение для входящих в отношение (3.13) величин, то после преобразований и вычислений получим:
2. Отношение (3.13) можно представить в виде
Так как по условию С1U1= C2U2 (см.(3.9)), то
Делаем проверку единиц измерения:
Расчет:
Ответ: После выемки стеклянной пластины разность потенциалов между пластинами конденсатора станет равной 875 В, а энергия увеличится в 4,38 раза.
Решение: Используем Закон Ома для полной цепи: где R – сопротивление внешней цепи; r – внутреннее сопротивление источника тока. Мощность Р, выделяемая во внешней цепи, определяется по формуле Таким образом, мощность зависит от внешнего сопротивления цепи R. Мощность будет максимальной при таком значении R, при котором производная dР/dR обращается в нуль. Возьмем первую производную и приравняем к нулю: Тогда получим R = r. Определим r. Максимальный ток возникает при коротком замыкании цепи, т.е. когда внешнее сопротивление R = 0. Исходя из этого, Подставив уравнение (3.17) в уравнение (3.15) и выполнив преобразования, получим: Проверка единиц измерения:
Расчет:
Ответ: Максимальная мощность, выделяемая во внешней цепи, равна 15 Вт. Пример 6. Сила тока в проводнике сопротивлением R = 20 Ом нарастает в течении времени Dt = 2 с по линейному закону от I0 = 0 до I = 6 А (рис. 3.6). Определить теплоту Q, выделившуюся в этом проводнике за вторую секунду.
Решение: Закон Джоуля – Ленца в виде Здесь сила тока I является некоторой функцией времени. В данном случае где
С учетом формулы (3.20) формула (3.19) примет вид Для определения теплоты, выделившейся за конечный интервал времени Dt, выражение (3.21) надо проинтегрировать в пределах от t1 до t2:
Проверка единиц измерения:
Расчет:
Ответ: За вторую секунду в проводнике выделится 420 Дж теплоты.
Задачи Таблица вариантов к контрольной работе №3
Темы задач (для каждого варианта): в первой задаче – взаимодействие зарядов, закон Кулона; во второй - напряженность электростатического поля; в третьей – потенциал, разность потенциалов электростатического поля, работа сил электростатического поля по перемещению зарядов; в четвертой – электроемкость, конденсаторы, энергия электростатического поля; в пятой – законы постоянного тока, соединение проводников; в шестой – работа и мощность тока, закон Джоуля-Ленца.
301. На расстоянии r = 20 см друг от друга расположены два точечных положительных заряда Q1 =10∙10-8 Кл и Q2 =15∙10-8 Кл. На каком расстоянии от меньшего заряда помещен пробный точечный заряд, если он находится в равновесии? Укажите, какой знак должен иметь этот заряд. 302. Точечные тела массами m1 = 5 г и m2 = 1 г заряжены. Заряд первого тела равен Q1 = 3∙10-12 Кл, заряд второго надо определить. Известно, что сила их кулоновского отталкивания уравновешивается силой гравитационного притяжения. 303. Два точечных заряда находятся в воде (e1 = 81) на некотором расстоянии друг от друга, взаимодействуя с некоторой силой. Во сколько раз необходимо изменить расстояние между ними, чтобы они взаимодействовали с такой же силой в среде с диэлектрической проницаемостью ε2 = 6. 304. В вершинах равностороннего треугольника со стороной а = 4 см находятся равные точечные заряды Q = 2×10-9 Кл. Найти равнодействующую сил, действующих на четвертый заряд Q4 = 10-9 Кл, помещенный на середине одной из сторон треугольника.
305. Два заряда взаимодействуют в вакууме на расстоянии r1 = 0,2 м с такой же силой, как и в трансформаторном масле на расстоянии r2 = 13,5 см. Какова диэлектрическая проницаемость трансформаторного масла? 306. Два шарика массами по m =1 мг подвешены на шелковых нитях длиной l = 1 м в одной точке. При сообщении шарикам зарядов они разошлись на r = 4 см. Определить заряд каждого шарика и силу их электростатического отталкивания. 307. На расстоянии d = 0,2 м находятся два точечных заряда: Q1 = -25 нКл и Q2 = 50 нКл. Определить силу F, действующую на заряд Q3 = 10 нКл, удаленный от обоих зарядов на одинаковое расстояние, равное d. 308. В вершинах правильного треугольника со стороной а = 20 см находятся заряды Q1 = 10 мкКл, Q2 = 20 мкКл и Q3 = -35 мкКл. Определить силу F, действующую на заряд Q1 со стороны двух других зарядов.
309. На шелковых нитях длиной l = 1 м висят, соприкасаясь друг с другом, два шарика малого диаметра; масса шариков по m = 0,1 г каждый. На какое расстояние разойдутся шарики, если каждому из них сообщить заряд Q = 4×10-9 Кл? Принять g = 10 м/с2. 310.Два одинаково заряженных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на угол a. Шарики погружают в масло. Какова плотность r масла, если угол расхождения нитей при погружении в масло остается неизменным? Плотность материала шариков rо = 1,5×103 кг/м3, диэлектрическая проницаемость масла e = 2,2. 311. Найти напряженность электрического поля в точке, лежащей посередине между точечными зарядами Q1 = 18×10-9 Кл и Q2 = 16×10-9 Кл. Расстояние между зарядами равно r = 0,2 м. 312. Электрическое поле создано двумя точечными зарядами Q1 = 5 нКл и Q2 = -10 нКл. Расстояние между зарядами d = 0,3 м. Определить напряженность электрического поля в точке, удаленной на r1 = 0,4 м от первого заряда ина r2 = 0,5 м от второго заряда. 313. В трех вершинах квадрата со стороной а = 0,5 м находятся одинаковые положительные заряды по Q = 5×10–9 Кл каждый. Найти напряженность поля в четвертой вершине. 314. Найти напряженность электрического поля на расстоянии r = 2×10-8 см от одновалентного иона. Одновалентный ион создает электрическое поле с напряженностью Е: Е = |q|/4*π*ε*ε0*r2 (1). Заряд одновалентного иона равен по абсолютной величине заряду электрона: |q| = 1,6*10-19 Кл. 1/4*π*ε0 = 9*109 м/Ф, ε = 1 диэлектрическая проницаемость воздуха. Тогда, подставив численные значения в выражение (1), получим окончательный результат: Е = 36*109 В/м = 36 ГВ/м. Ответ: Е = 36*109 В/м = 36 ГВ/м. 315. Электрическое поле создано двумя точечными зарядами Q1 = 40 нКл и Q2 = -10 нКл, находящимися на расстоянии d = 10 см друг от друга. Определить напряженность электрического поля в точке, удаленной от первого заряда на r1 = 12 см и от второго заряда на r2 = 6 см. 316. Тонкая нить несет равномерно распределенный по длине заряд (t = 20 мкКл/м). Вблизи средней части нити на расстоянии r = 1 см, малом по сравнению с ее длиной, находится точечный заряд q = 0,1 мкКл. Определить силу, действующую на заряд. 317. Расстояние между двумя длинными тонкими проволоками, расположенными параллельно друг другу, d = 20 см. Проволоки равномерно заряжены разноименными зарядами с линейной плотностью t = 150 нКл/м. Какова напряженность поля в точке, удаленной на r = 30 см как от первой, так и от второй проволоки. 318. Тонкий стержень длиной l = 20 см имеет линейную плотность заряда t = 200 нКл/м. Найти напряженность электрического поля в точке, находящейся на расстоянии r = 50 см от стержня против его середины.
319. Электрическое поле создано двумя бесконечными параллельными пластинами, несущими одинаковый равномерно распределенный по площади заряд (s = 10 нКл/м2). Определить напряженность E электрического поля: 1) между пластинами, 2) вне пластин. 320. Электрическое поле создано двумя бесконечными параллельными пластинами, несущими равномерно распределенный по площади заряд с поверхностными плотностями s1 = 10 нКл/м2 и s2 = 30 нКл/м2. Определить напряженность E электрического поля: 1) между пластинами; 2) вне пластин. 321. На окружности радиусом R = 20 см на одинаковом расстоянии расположены электрические заряды Q1 = 4,8×10-6 Кл, Q2 = Q3 = 1,6×10-6 Кл, Q4 = -1,6×10-6 Кл. Определить потенциал электрического поля, образованного всеми зарядами в центре окружности. 322. Два точечных электрических заряда Q1 = 2,64×10-9 Кл и Q2 = 3,3×10-9 Кл находятся в вакууме на расстоянии r1 = 0,6 м друг от друга. Какую работу надо совершить, чтобы сблизить эти заряды до расстояния r2 = 25 см. 323. Определить потенциал электрического поля в точке, удаленной от зарядов Q1 = - 0,2 мкКл и Q2 = 0,5 мкКл соответственно на расстояния r1 = 15 см и r2 = 25 см. 324. На какое расстояние могут сблизиться два электрона, если они движутся навстречу друг другу с относительной скоростью 108 см/с? 325. Шарик массой т = 0,1 г и зарядом q =10×10-9 Кл перемещается из точки А с потенциалом jА = 1600 В, в точку Б, потенциал которой равен нулю. Чему равна его скорость в точке А, если в точке Б она стала равной VБ = 40 см/с? 326. Бесконечная длинная тонкая нить несет равномерно распределенный по длине заряд с линейной плотностью t = 0,1 мкКл/м. Определить разность потенциалов двух точек поля, удаленных от нити на расстояния r1 = 3 см и r2 = 5 см. 327. Вычислить потенциальную энергию системы двух точечных зарядов Q1 = 10 нКл и Q2 = 1 нКл, находящихся на расстоянии r = 1 см друг от друга. 328. Металлический шарик диаметром d = 2 см заряжен отрицательно до потенциала j = 300 В. Сколько электронов находится на поверхности шарика? 329. 50 одинаковых капель ртути, заряженных до потенциала j = 20 В, сливаются в одну большую каплю. Каков потенциал образовавшейся капли? 330.На расстоянии r1 = 4 см от бесконечно длинной заряженной нити находится точечный заряд q = 1×10-9 Кл. Под действием поля заряд перемещается до расстояния r2 = 2 см, при этом совершается работа А = 5×10‑6 Дж. Найти линейную плотность заряда t нити. 331. Разность потенциалов между пластинами плоского конденсатора равна U = 90 В. Площадь каждой пластины S = 60 см2, заряд Q = 10-9 Кл. На каком расстоянии находятся пластины друг от друга? 332. Электрон, пройдя в плоском конденсаторе путь от одной пластины к другой, приобретает скорость V = 108 см/с. Расстояние между пластинами d = 5,3 мм. Найти разность потенциалов между пластинами, напряженность электрического поля внутри конденсатора и поверхностную плотность заряда на пластинах. 333. Два одинаковых плоских воздушных конденсатора емкостью С = 100 пФ каждый соединены в батарею последовательно. Определить, насколько изменится емкость батареи, если пространство между пластинами одного из конденсаторов заполнить парафином с диэлектрической проницаемостью e = 2. 334. К плоскому воздушному конденсатору площадь пластин которого S = 100 см2, приложено напряжение U = 150 В, при этом заряд конденсатора оказался равным Q = 10-9 Кл. Определить емкость конденсатора, энергию, запасенную в нем, и расстояние между пластинами. 335. Между пластинами плоского конденсатора расстояние d1 = 2 см, разность потенциалов U1 = 300 В. Как изменится разность потенциалов, если пластины раздвинуть до расстояния d2 = 4 см (поле считать однородным)? 336. Плоский конденсатор с площадью пластин S = 200 см2 каждая заряжен до разности потенциалов U = 2 кВ. Расстояние между пластинами d = 2 см; диэлектрик – стекло имеет диэлектрическую проницаемость e = 7. Определить энергию поля конденсатора и плотность энергии поля. 337. Конденсатор емкостью С = 30 мкФ был заряжен до разности потенциалов U = 60 В. После отключения от источника питания конденсатор был параллельно соединен с другим незаряженным конденсатором емкостью С2 = 50 мкФ. Какое количество энергии первого конденсатора израсходуется на образование искры в момент присоединения второго конденсатора? 338. Плоский воздушный конденсатор емкостью С = 1,1×10-8 Ф заряжен до разности потенциалов U = 300 В. После отключения от источника напряжения расстояние между пластинами конденсатора увеличили в 2 раза. Определить: 1) разность потенциалов на обкладках конденсатора после их раздвигания; 2) работу внешних сил по раздвиганию пластин. 339. Вычислить энергию электростатического поля металлического шара, которому сообщен заряд Q = 10 нКл, если диаметр шара D = 20 см. 340. Пространство между пластинами плоского конденсатора объемом V = 20 см3 заполнено диэлектриком (e =7). Пластины конденсатора присоединены к источнику напряжения. При этом поверхностная плотность связанных зарядов на диэлектрике s = 8×10-6 Кл/м2. Какую работу надо совершить против сил электрического поля, если удаление диэлектрика производится после отключения источника напряжения? 341.Определить плотность тока в железном проводе длиной l = 10 м, если провод находится под напряжением U = 120 В. Удельное сопротивление железа r = 9,8×10-8 Ом×м. 342. Участок электрической цепи составлен из трех кусков провода одинаковой длины, изготовленных из одного и того же материала, соединенных последовательно. Сечения кусков провода равны S1 = 2 мм2, S2 = 4 мм2 и S3 = 6 мм2. Разность потенциалов на концах участка U = 12 В. Найти разность потенциалов на каждом куске провода. 343.Аккумуляторная батарея, замкнутая на реостат сопротивлением R = 20 Ом, создает в нем ток I1 = 1,5 А. Если сопротивление реостата увеличить в 4 раза, то ток станет равным I2 = 0,5 А. Определить ЭДС и внутреннее сопротивление источника, а также силу тока короткого замыкания. 344. Две группы из трех последовательно соединенных элементов соединены параллельно. ЭДС каждого элемента e = 1,2 В, внутреннее сопротивление r = 0,2 Ом. Полученная батарея замкнута на внешнее сопротивление R = 1,5 Ом. Найти силу тока во внешней цепи. 345.Какое сопротивление R нужно подключить к n = 5 одинаковым последовательно соединенным источникам с внутренним сопротивлением r = 0,2 Ом, чтобы потребляемая полезная мощность была максимальной? 346. Источник постоянного тока с ЭДС e =120 В и внутренним сопротивлением r = 1 Ом включен в цепь. Какую наибольшую мощность может развить источник во внешней части цепи? При каком сопротивлении внешней части цепи это происходит? Чему равен КПД источника в этом случае? 347.Определить число электронов, проходящих за время t = 10 с через поперечное сечение площадью S = 10 мм2 железной проволоки с удельным сопротивлением r = 9,8×10-8 Ом, длиной l = 20 м при напряжении на ее концах U = 20 В, а также мощность тока. 348.ЭДС батареи e = 12 В. При силе тока I = 4 А КПД батареи h = 0,6. Определить внутреннее сопротивление батареи. 349.ЭДС батареи e = 6 В. Наибольшая сила тока, которую может дать батарея, 350. ЭДС батареи e = 36 В, внутреннее сопротивление r = 3 Ом. Найти сопротивление внешней цепи, если известно, что в ней выделяется мощность P = 20 Вт. Определить КПД батареи. 351. Сила тока в проводнике сопротивлением R = 20 Ом нарастает в течение времени Dt = 2 с по линейному закону от I1 = 0 до I2 = 6 А. Определить количество теплоты Q1, выделившееся в этом проводнике за первую секунду; количество теплоты Q2, выделившееся за вторую секунду; а также количество теплоты Q, выделившееся за две секунды. 352. За время t = 30 с при равномерно возрастающей силе тока от нуля до некоторого максимума, в проводнике сопротивлением R = 5 Ом выделилось количество теплоты Q = 4 кДж. Определить скорость нарастания силы тока и заряд, протекающий в проводнике. 353. Сила тока в проводнике сопротивлением R = 8 Ом за время t = 20 с равномерно возрастает от I1 = 2 А до I2 = 10 А. Определить количество теплоты, выделившееся за это время и заряд, протекающий в проводнике. 354. В проводнике за время t = 40 с при равномерном возрастании силы тока от I1 = 1 А до I2 = 5 А выделилось количество теплоты Q = 5 кДж. Найти сопротивлениепроводника и заряд, протекающий в проводнике. 355. За время t = 8 с при равномерно возрастающей силе тока в проводнике сопротивлением R = 4 Ом выделилось количество теплоты Q = 500 Дж. Определить заряд q, протекающий в проводнике, если сила тока в момент времени t = 0 равна I0 = 0,5 А. 356. Резистор сопротивлением R = 8 Ом подключен к двум параллельно соединенным источникам тока с ЭДС e1 = 2,2 В и e2 = 2,4 В и внутренними сопротивлениями r1 = 0,8 Ом и r2 = 0,2 Ом. Определить силу тока I в этом резисторе и напряжение U на зажимах второго источника тока. 357.Сила тока в проводнике сопротивлением R = 10 Ом изменяется со временем по закону 358.Сила тока в проводнике изменяется со временем по закону 359.Определить количество теплоты Q, выделившееся за время t = 10 с в проводнике сопротивлением R = 10 Ом, если сила тока в нем, равномерно уменьшаясь, изменилась от I1 = 10 А до I2 = 0. 360.Сила тока в цепи изменяется со временем по закону
Электромагнетизм |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 794. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 ,
, – электрическая постоянная; r – расстояние между зарядами.
– электрическая постоянная; r – расстояние между зарядами.


 – сила, действующая на пробный заряд;
– сила, действующая на пробный заряд;
 ,
, ,
, ;
;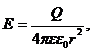
 .
. электрического поля и электрической индукцией
электрического поля и электрической индукцией 
 .
.
 ,
, .
. (при r < R);
(при r < R); ,
,  ,
,  ,
, 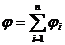 ,
, ,
,  - напряженность и потенциал в данной точке электрического поля, создаваемого зарядом.
- напряженность и потенциал в данной точке электрического поля, создаваемого зарядом. или
или  в общем случае;
в общем случае; в случае однородного поля;
в случае однородного поля; в случае поля, обладающего центральной или осевой симметрией.
в случае поля, обладающего центральной или осевой симметрией. ,
, ,
, - единичный вектор, направленный из точки, где находится заряд dQ, в рассматриваемую точку поля.
- единичный вектор, направленный из точки, где находится заряд dQ, в рассматриваемую точку поля. .
.
 ,
, - плечо диполя (векторная величина, направленная от отрицательного заряда к положительному и численно равная расстоянию между зарядами).
- плечо диполя (векторная величина, направленная от отрицательного заряда к положительному и численно равная расстоянию между зарядами). ,
,  ,
, – разность потенциалов пластин конденсатора.
– разность потенциалов пластин конденсатора. ;
; ,
, ,
,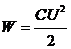 ,
, или
или  ;
;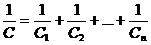 или
или  .
. ,
,  ,
, ,
,  ,
, - при последовательном соединении;
- при последовательном соединении; - при параллельном соединении,
- при параллельном соединении, - для участка цепи, не содержащего ЭДС, где j1-j2 =U – разность потенциалов на концах участка цепи; R – сопротивление участка цепи;
- для участка цепи, не содержащего ЭДС, где j1-j2 =U – разность потенциалов на концах участка цепи; R – сопротивление участка цепи; - для участка цепи, содержащего ЭДС, где e - ЭДС источника тока; Rполн – полное сопротивление участка (сумма внешних и внутренних сопротивлений);
- для участка цепи, содержащего ЭДС, где e - ЭДС источника тока; Rполн – полное сопротивление участка (сумма внешних и внутренних сопротивлений); для замкнутой (полной) цепи, где R – внешнее сопротивление цепи; r – внутреннее сопротивление цепи.
для замкнутой (полной) цепи, где R – внешнее сопротивление цепи; r – внутреннее сопротивление цепи. - первый закон;
- первый закон; - второй закон,
- второй закон, - алгебраическая сумма сил токов, сходящихся в узле;
- алгебраическая сумма сил токов, сходящихся в узле;  алгебраическая сумма произведений сил токов на сопротивления участков;
алгебраическая сумма произведений сил токов на сопротивления участков; 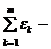 алгебраическая сумма ЭДС.
алгебраическая сумма ЭДС. .
. .
. .
.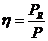 .
.
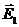 и
и  полей, создаваемых каждым зарядом в отдельности:
полей, создаваемых каждым зарядом в отдельности: .
. , (3.1)
, (3.1) (3.2)
(3.2) , (3.3)
, (3.3) и
и 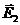 в треугольнике А
в треугольнике А  .
.
 . (3.4)
. (3.4) . (3.5)
. (3.5) или
или  .
.
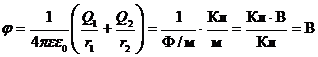 .
.
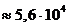 B/м;
B/м;
 .
. .
. .
.

 .
.
 сил поля по перемещению заряда между этими точками поля, то есть
сил поля по перемещению заряда между этими точками поля, то есть
 .
. , (3.7)
, (3.7) , (3.8)
, (3.8) .
. .
. .
.
 , (3.9)
, (3.9) , (3.10)
, (3.10) . (3.11)
. (3.11) . (3.12)
. (3.12) .
. . (3.13)
. (3.13) .
. .
. .
. .
.

 Пример 5. Определить максимальную мощность, которая может выделяться во внешней цепи, питаемой от батареи с ЭДС 12 В, если наибольшая сила тока, которую может дать батарея, равна
Пример 5. Определить максимальную мощность, которая может выделяться во внешней цепи, питаемой от батареи с ЭДС 12 В, если наибольшая сила тока, которую может дать батарея, равна 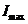 = 5 А.
= 5 А. , (3.14)
, (3.14) . Преобразуем это выражение, используя формулу (3.14):
. Преобразуем это выражение, используя формулу (3.14): . (3.15)
. (3.15) . (3.16)
. (3.16) , откуда
, откуда 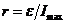 , значит
, значит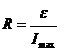 . (3.17)
. (3.17) . (3.18)
. (3.18)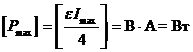 .
. .
.
 справедлив для постоянного тока (I = const). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого интервала времени и записывается в виде
справедлив для постоянного тока (I = const). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого интервала времени и записывается в виде . (3.19)
. (3.19) , (3.20)
, (3.20) – сила тока в начальный момент времени, k – коэффициент пропорциональности, характеризующий скорость изменения силы тока. Как видно из рис. 3.6
– сила тока в начальный момент времени, k – коэффициент пропорциональности, характеризующий скорость изменения силы тока. Как видно из рис. 3.6 .
. . (3.21)
. (3.21) .
. .
. Дж.
Дж. Определить максимальную мощность, которая выделится во внешней цепи, и КПД батареи.
Определить максимальную мощность, которая выделится во внешней цепи, и КПД батареи. , где
, где  = 20 А, a = 102 с-1. Определить количество теплоты, выделившееся в проводнике за время t = 10-2 с.
= 20 А, a = 102 с-1. Определить количество теплоты, выделившееся в проводнике за время t = 10-2 с. . Найти заряд Q, проходящий через поперечное сечение проводника за время t, равное половине периода T, если начальная сила тока I0 = 1 А, циклическая частота w = 50p с-1.
. Найти заряд Q, проходящий через поперечное сечение проводника за время t, равное половине периода T, если начальная сила тока I0 = 1 А, циклическая частота w = 50p с-1.