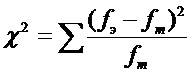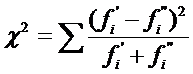Оценка достоверности отличий.

Одной из наиболее часто встречающихся задач при обработке данных является оценка достоверности отличий между двумя или более рядами значений. В математической статистике существует ряд способов для этого.

Степень выявленного различия желательно оценивать, опираясь на содержательные критерии. Вместе с тем, для психологического исследования весьма характерно наличие множества показателей, которые, по существу, являются условными баллами, и валидность оценивания с их помощью еще предстоит доказать. Чтобы избежать большей произвольности, в таких случаях также приходится опираться на статистические параметры.

Пожалуй, наиболее распространено для этого использование сигмы. Разницу между двумя значениями в одну сигму и более можно считать достаточно выраженной. Если сигма подсчитана для ряда значений более 35, то достаточно выраженной можно рассматривать и разницу в 0.5 сигмы. Однако, для ответственных выводов о том, насколько велика разница между значениями, лучше использовать строгие критерии.

При использовании в качестве измерительных интервальных щкал достоверность различий средних арифметических можно оценить по достаточно эффективному параметрическому критерию Стьюдента (t). Он вычисляется по формуле:

где: M₁ и M₂ – значения сравниваемых средних арифметических, m₁ и m₂ – соответствующие величины статистических ошибок средних арифметических.

Значения критерия Стьюдента для трех уровней значимости (p) приведены в Приложении № . Число степеней свободы определяется по формуле:d = n₁ + n₂ – 2, где n₁ и n₂ – объемы сравниваемых выборок. С уменьшением объемов выборок (n < 10) критерий Стьюдента становится чувствительным к форме распределения исследуемого признака в генеральной совокупности. Поэтому в сомнительных случаях рекомендуется использовать непараметрические методы или сравнивать полученные значения с критическими (приведенными в таблице) для более высокого уровня значимости.

Решение о достоверности различий принимается в том случае, если вычисленная величина t_d превышает табличное значение для данного числа степеней свободы. В тексте публикации или научного отчета указывают наиболее высокий уровень значимости из трех: 0.05, 0.01 или 0.001. Если превышены 0.05 и 0.01, то пишут (обычно в скобках) р = 0.01 или р < 0.01. Это означает, что оцениваемые различия все же случайны только с вероятностью не более 1 из 100 шансов. Если превышены табличные значения для всех трех уровней: 0.05, 0.01 или 0.001, то указывают р = 0.001 или р < 0.001, что означает случайность выявленных различий между средними не более 1 из 1000 шансов.

Следует помнить, что при любом численном значении критерия достоверности различий между средними этот показатель оценивает не степень выявленного различия (она оценивается по самой разности между средними), а лишь статистическую достоверность его, т.е. право распространять полученный на основе сопоставления выборок вывод о наличии разницы на все явления (весь процесс) в целом. Низкий вычисленный критерий различия не может служить доказательством отсутствия различия между двумя признаками (явлениями) ибо его значимость (степень вероятности) зависит не только от величины средних, но и от численности сравниваемых выборок. Он говорит не об отсутствии различия, а о том, что при данной величине выборок оно статистически недостоверно: слишком велик шанс, что разница при данных условиях определения случайна, слишком мала вероятность его достоверности.

Для порядковых и номинальных шкал применяются непараметрические критерии, с помощью которых сравниваются не обобщающие показатели выборок (в случае с интервальными шкалами в качестве таковых выступают параметры распределения), а сопоставляются распределения частот. Непараметрические критерии можно применять и для интервальных данных, т.к. эти критерии не требуют анализа формы распределения, т.е. не рассчитаны только на нормальное распределение (подобно критерию Стьюдента и Фишера). Наконец, применение их предпочтительно с точки зрения простоты математического аппарата.

Критерий χ² («хи-квадрат») Пирсона используется для сравнения частот двух распределений: двух эмпирических или эмпирического и теоретического.

где ƒэ  - эмпирическая частота (частоты), соответствующая определённому (определённым) разрядам;

 ƒт - теоретическая (ожидаемая) частота.

где ƒ_i^’ и ƒ_i^’’ – частоты двух сопоставляемых выборок.

Полученные величины критерия сравниваются с табличными значениями для того или иного уровня значимости (Табл. Приложения 1).

где Cumƒ_i^’ и Cumƒ_i^’’ – накопленные к i–му разряду частоты.

Многофункциональные критерии (Сидоренко Е.В., 1996, гл. 5) используются по отношению к самым разнообразным признакам, выборкам и задачам. Они построены на сопоставлении долей, выраженных в долях единицы или в процентах. Суть их состоит в определении того, какая доля наблюдений (реакций, выборов, испытуемых и т.п.) в данной выборке характеризуется интересующим исследователя эффектов и какая доля этим эффектом не характеризуется.

Биномиальный критерий m применяется в том случае, когда обследована лишь одна выборка испытуемых объёмом не более 300 (в некоторых задачах – не более 50) единиц. Он позволяет оценить, насколько эмпирическая частота (m) наблюдений, в которых проявляется интересующий нас эффект, превышает теоретическую, среднестатистическую или какую-то заданную частоту. Порядок его применения прост: эмпирическая частота m сравнивается с критическим значением m_кр, найденным с помощью Таблицы №__ (Приложение 1). Если m равен или превышает m_кр, то различия достоверны.

где φ₁ – угол, соответствующий большей % доле;

φ₂ - угол, соответствующий меньшей % доле;

n₁ – количество наблюдений в выборке 1;

n₂ – количество наблюдений в выборке 2.

По таблицам Приложения 1 либо определяем, какому уровню значимости соответствует φ^* (Таблица №.__), либо сравниваем с критическими значениями φ^*, соответствующим уровням значимости, принятым в психологии: φ^*_0.05 = 1,64;  φ^*_0.01 = 2,31.