Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Релаксационный генератор на основе тиратрона
Для поддержания тлеющего разряда в тиратроне необходимо некоторое напряжение Uг между катодом и сеткой. Во время разряда через лампу идет большой ток и ее электрическое сопротивление мало. Если напряжение между катодом и сеткой станет меньше некоторого напряжения гашения, то тлеющий разряд гаснет, ток уменьшается почти до нуля, а сопротивление лампы становится очень большим. Фактически это означает размыкание цепи на промежутке катод-сетка. На основе таких газоразрядных приборов можно сконструировать специфические генераторы электрических колебаний - релаксационные генераторы. Рассмотрим принцип работы такого генератора (рис. 4.4). При включении ключа К напряжение на ёмкости С равно Uc =0, так как конденсатор не может сразу зарядиться. Первоначально все напряжение приложено к сопротивлению R. Ток, протекающий по этому сопротивлению, заряжает конденсатор до напряжения
Рис 4.4. Схема релаксационного генератора на основе тиратрона
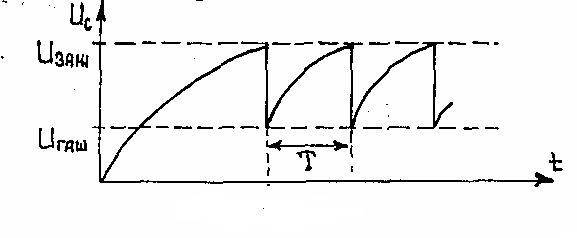
Рис. 4.5.Пилообразное напряжение
Определим период колебания такого генератора. Так как напряжение на конденсаторе С:
Интегрируя уравнение (4.2), получим аналитическое выражение 
Деля левую и правую части (4.3) на С, получим:
Так как разряд конденсатора через неоновую лампу происходит почти мгновенно, то за период Т конденсатор зарядится от
Тогда:
Из (4.5) можно получить формулу для расчёта периода Т:
Примечание: дифференциальное уравнение (4.2) может быть решено с помощью математической системы MathCAD. Результат решения этого уравнения в системе MathCAD показан ниже.
Рис. 4.6. Пример решения с помощью математической системы MathCAD Экспериментальная установка
Экспериментальная установка собрана по схеме, показанной на рис.4.7. Используя разъёмы А и В, на установке могут быть собраны две схемы: 1. Схема определения потенциала гашения 2. Схема релаксационного генератора (цепь собирается с помощью соединительных проводов 1 и 2). На стенде также имеется электрический секундомер, с помощью которого можно определить период колебания практически Тп
где N – число колебаний, t – время N колебаний. При достаточно высокой частоте колебаний можно выбрать N = 10, при низкой частоте колебаний
Рис.4.7. Схема экспериментальной установки
Параметры схемы приведены в табл. 4.1. Таблица 4.1
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 695. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||
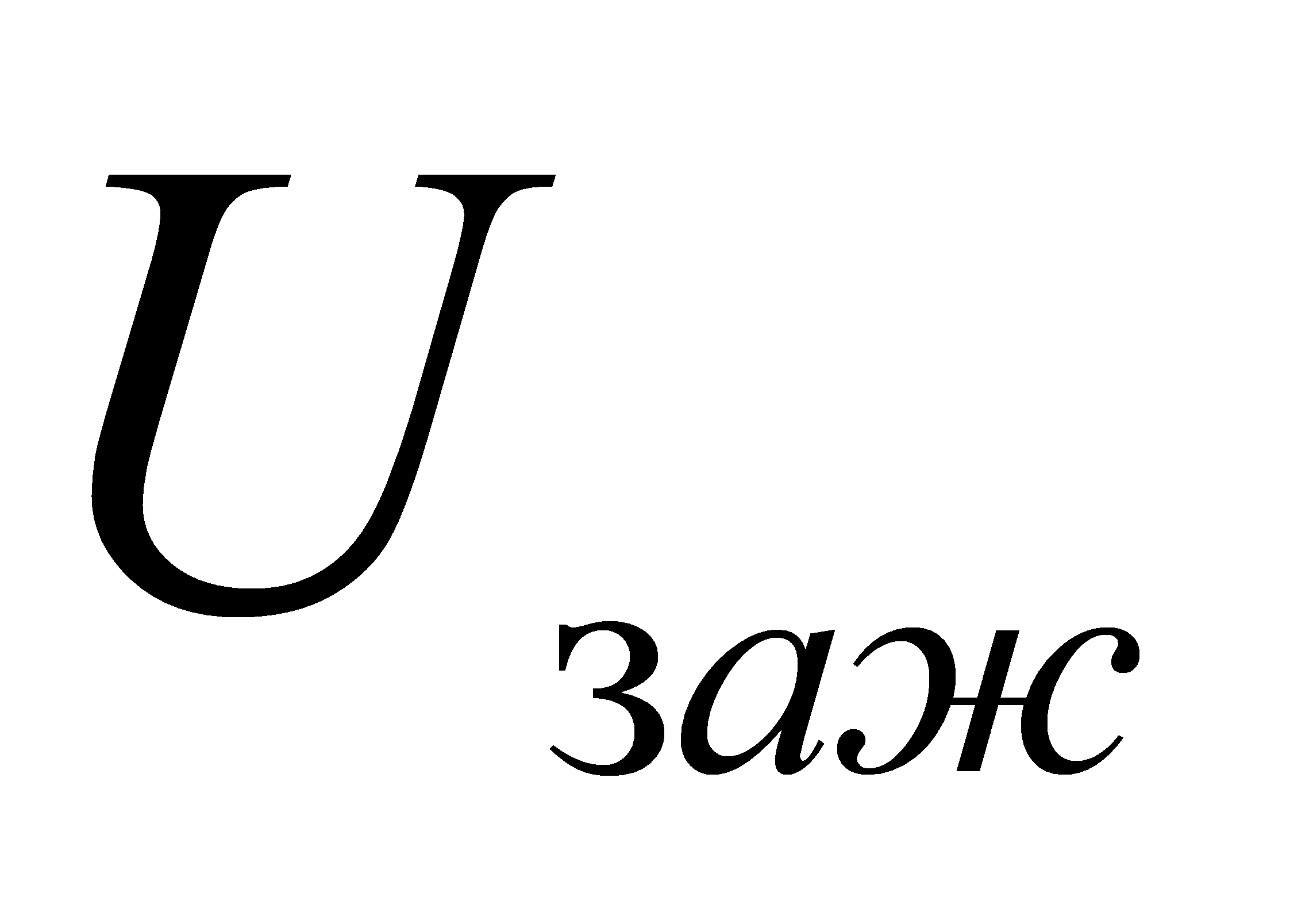 зажигания разряда на промежутке катод-сетка тиратрона. Лампа зажигается и сопротивление ее уменьшается, через лампу конденсатор разряжается. Разряд конденсатора происходит до напряжения
зажигания разряда на промежутке катод-сетка тиратрона. Лампа зажигается и сопротивление ее уменьшается, через лампу конденсатор разряжается. Разряд конденсатора происходит до напряжения 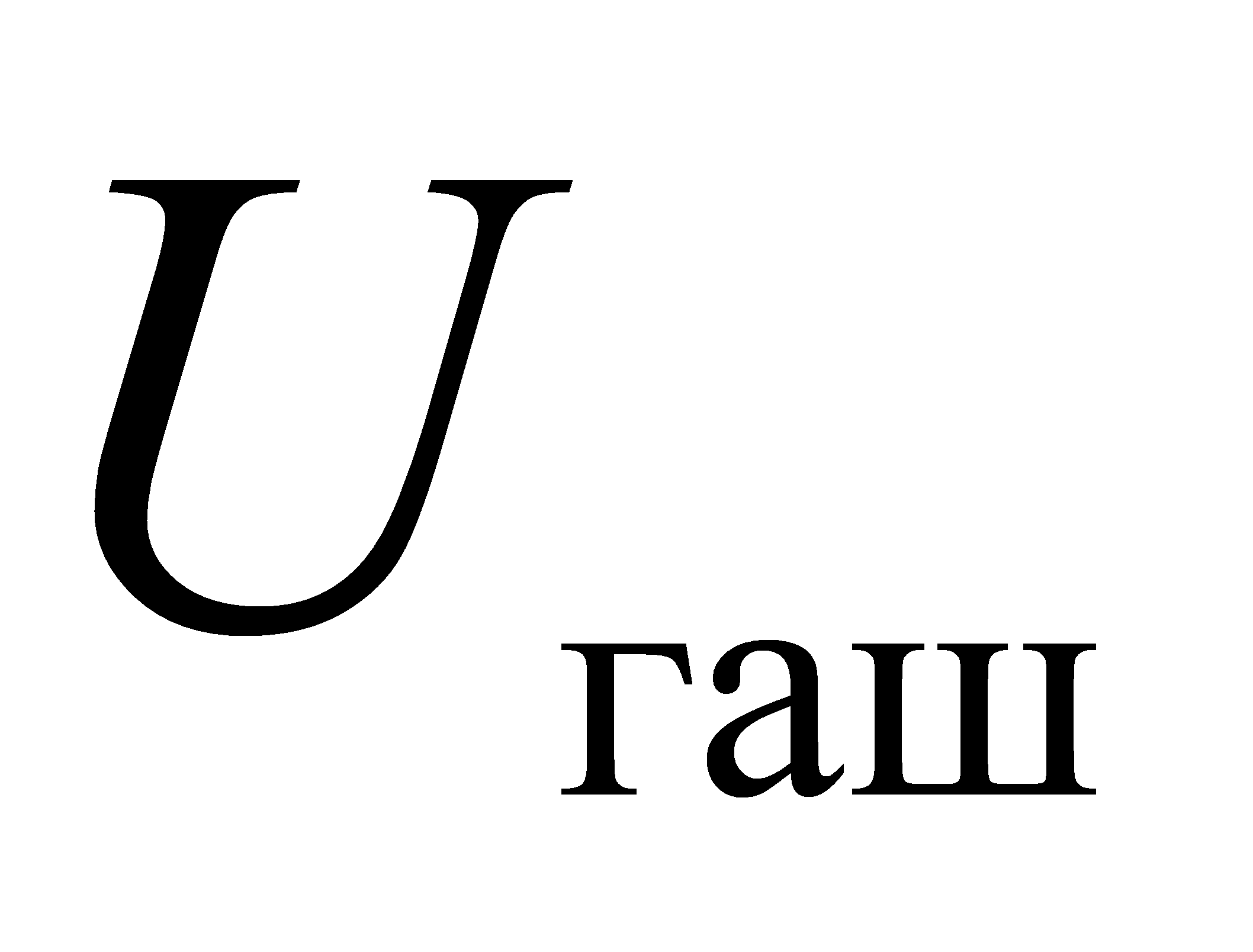 , цепь на промежутке катод-сетка тиратрона размыкается. После этого конденсатор снова начинает заряжаться и процесс повторяется (рис. 4.5).
, цепь на промежутке катод-сетка тиратрона размыкается. После этого конденсатор снова начинает заряжаться и процесс повторяется (рис. 4.5).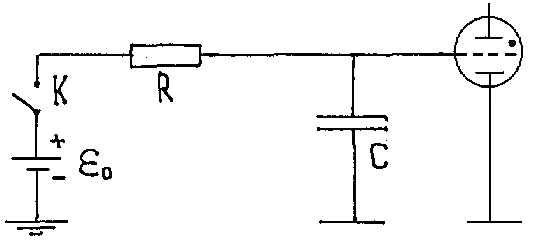
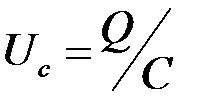 , а ток, протекающий по сопротивлению R:
, а ток, протекающий по сопротивлению R: 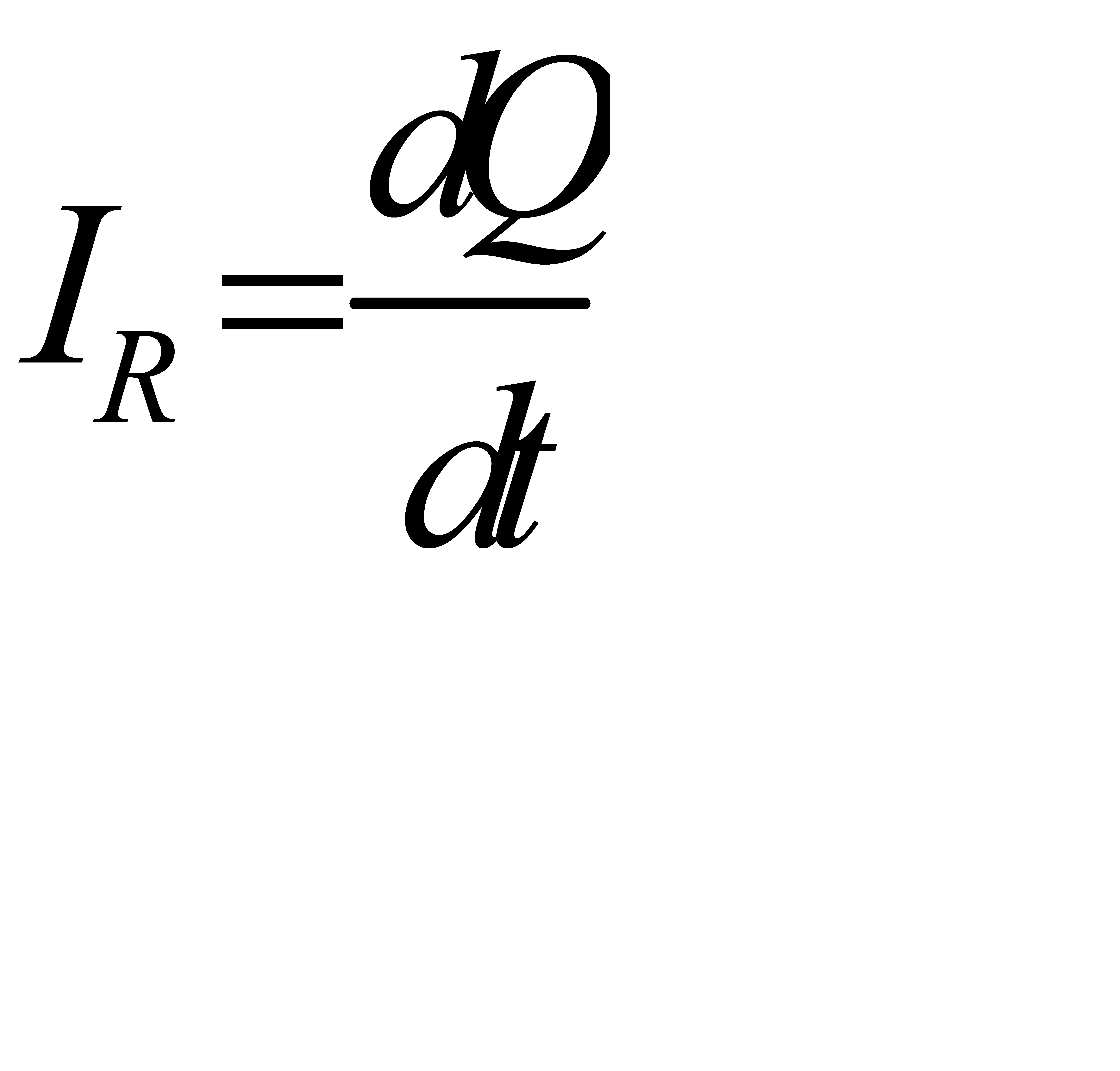 , то из второго правила Кирхгофа имеем:
, то из второго правила Кирхгофа имеем: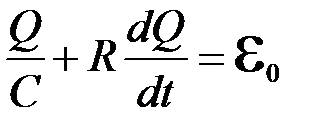 . (4.2)
. (4.2)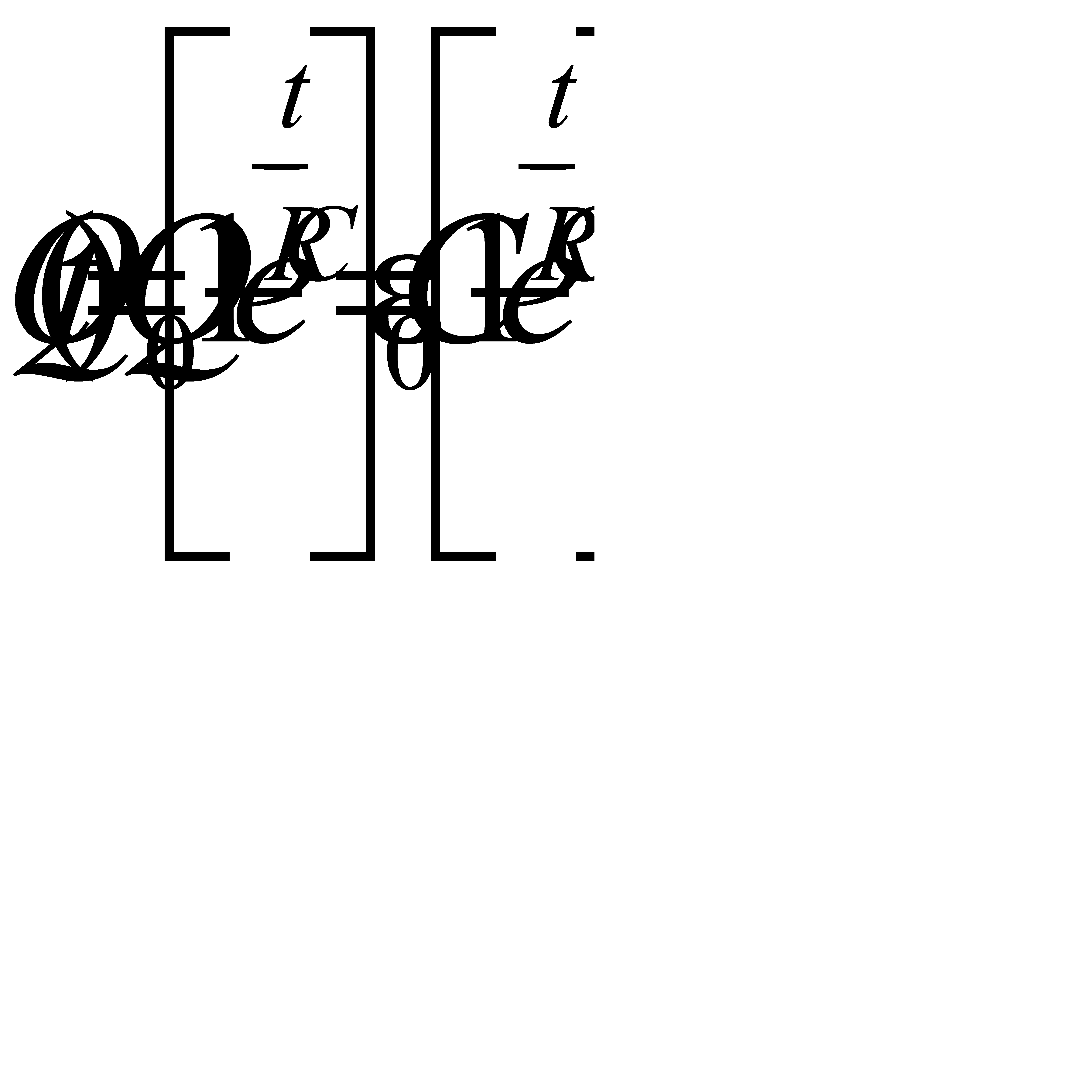 . (4.3)
. (4.3)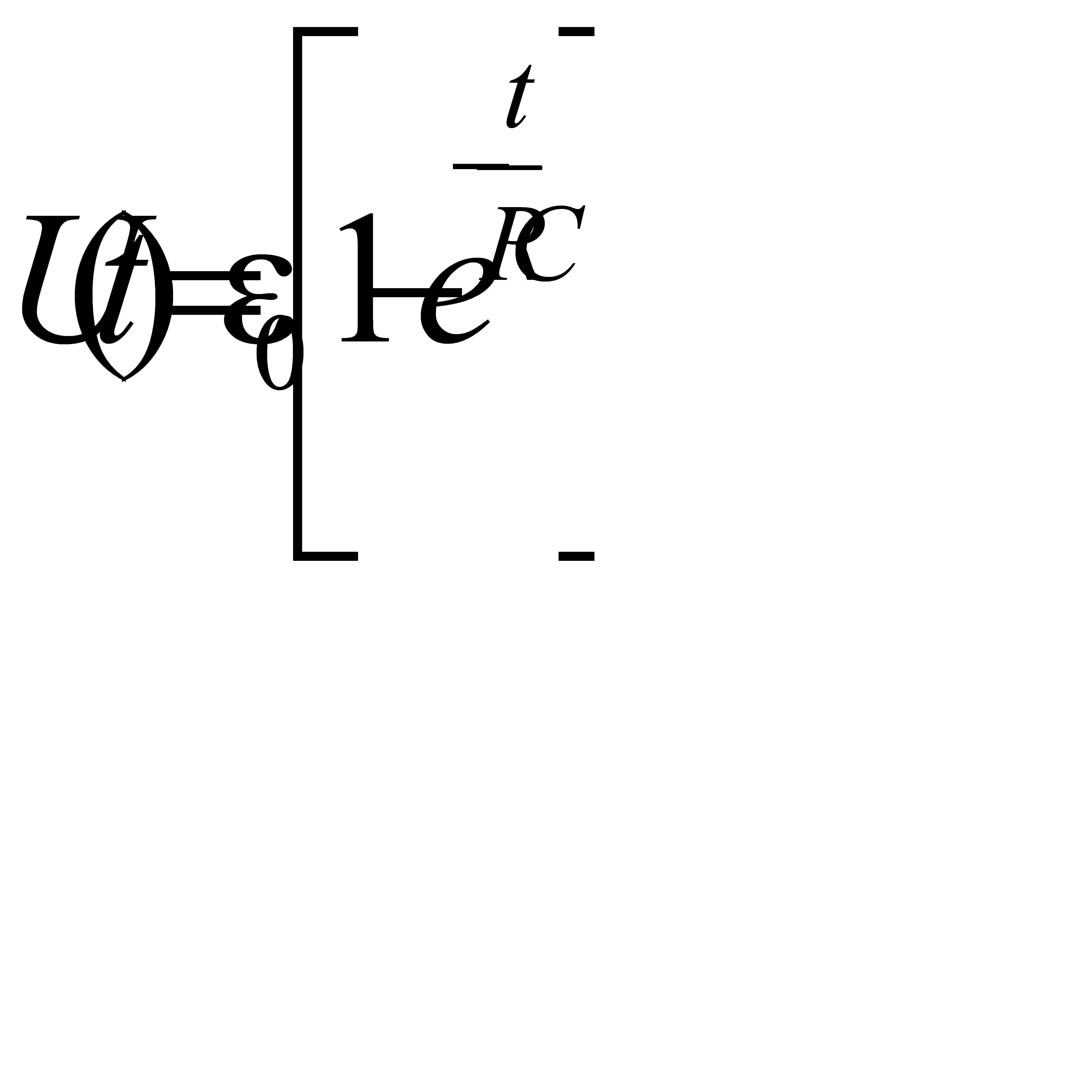 . (4.4)
. (4.4)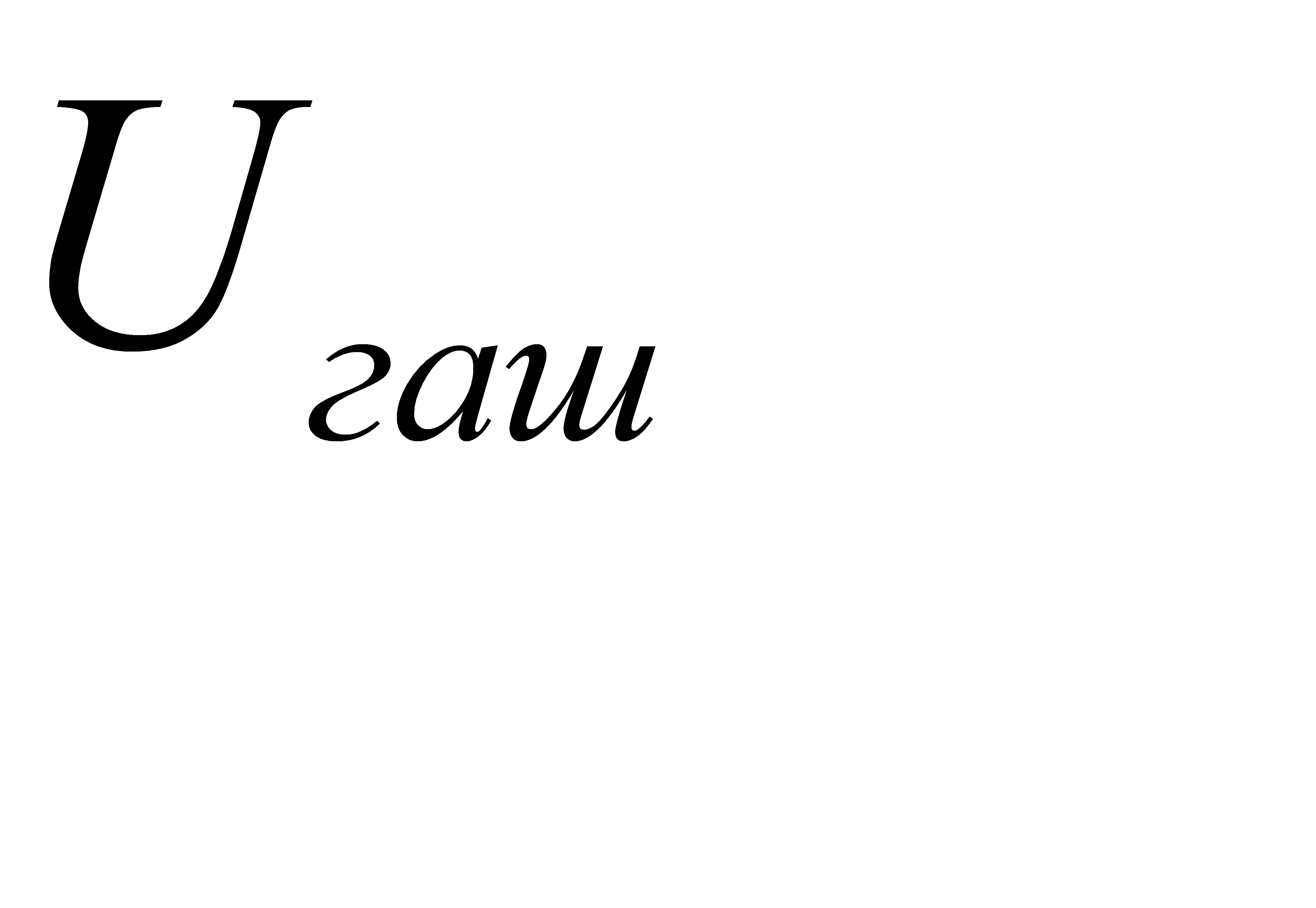 до
до 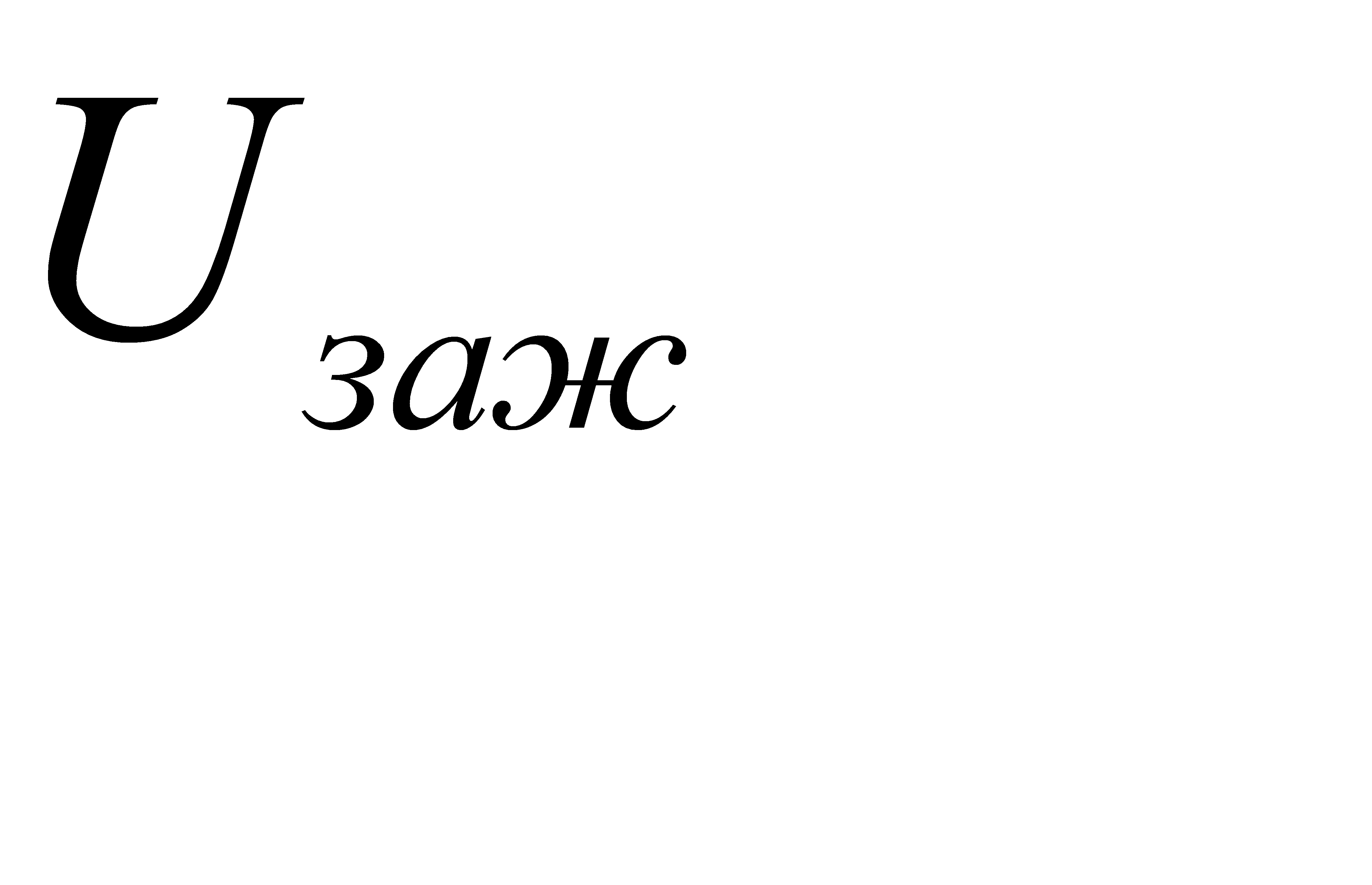 .
.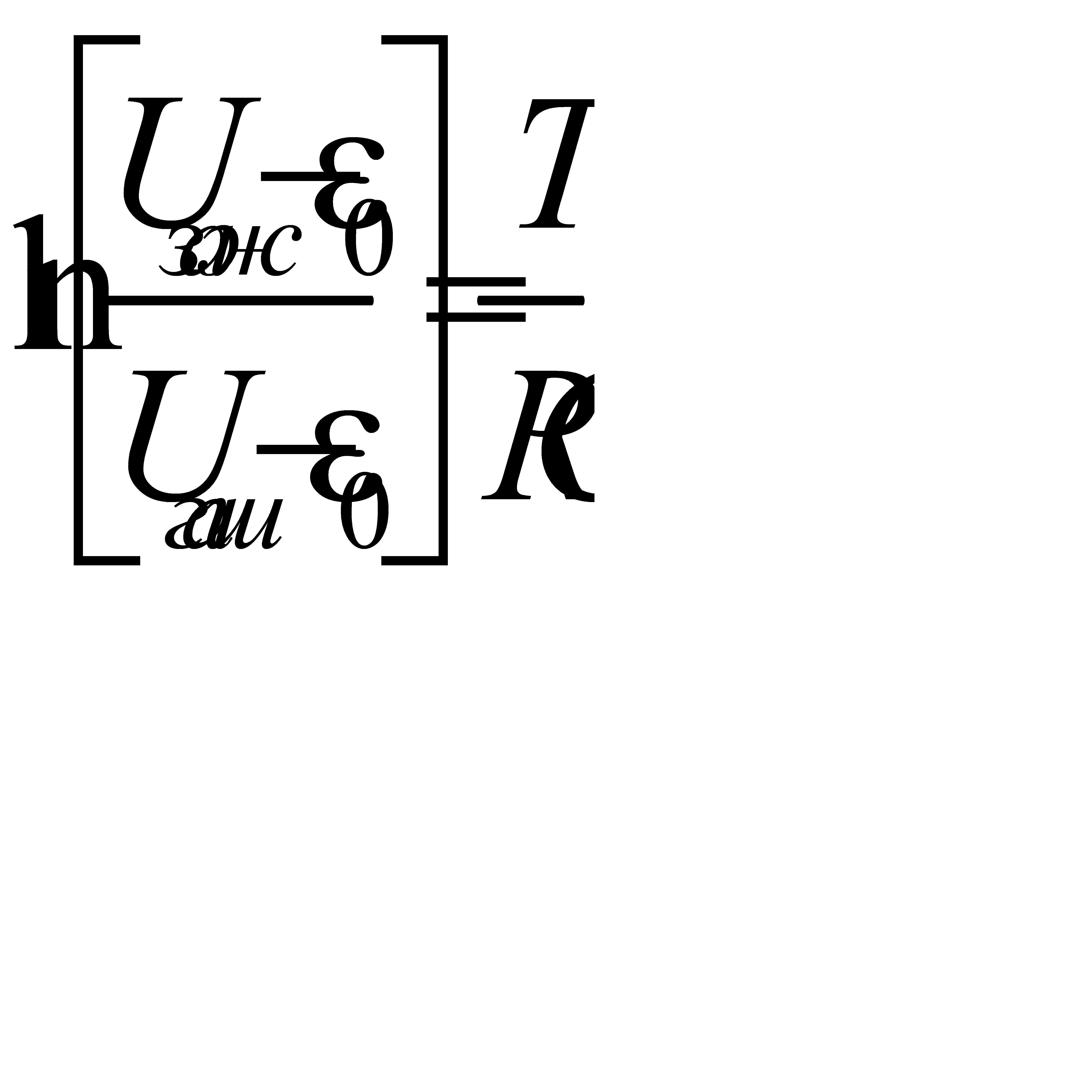 . (4.5)
. (4.5)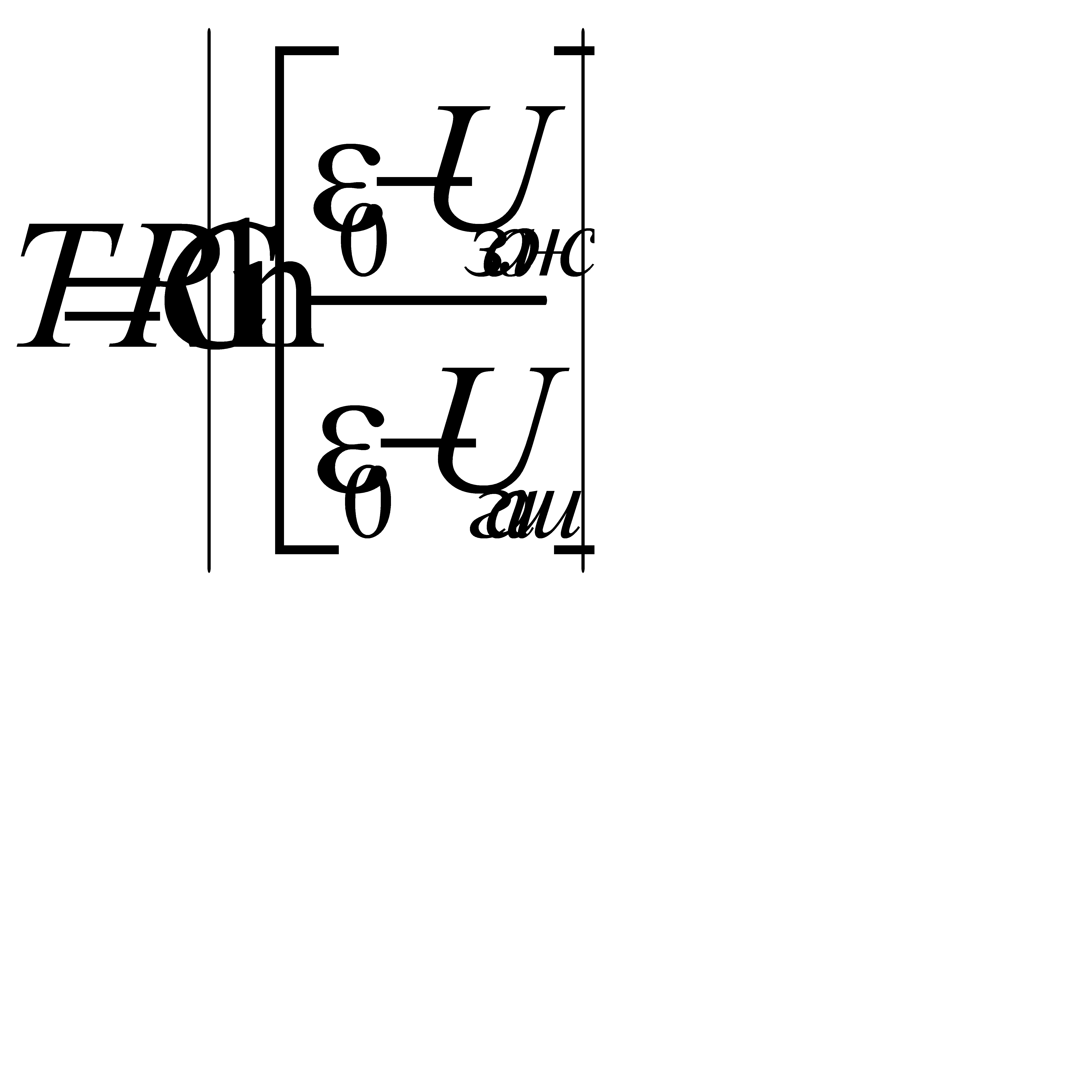 . (4.6)
. (4.6)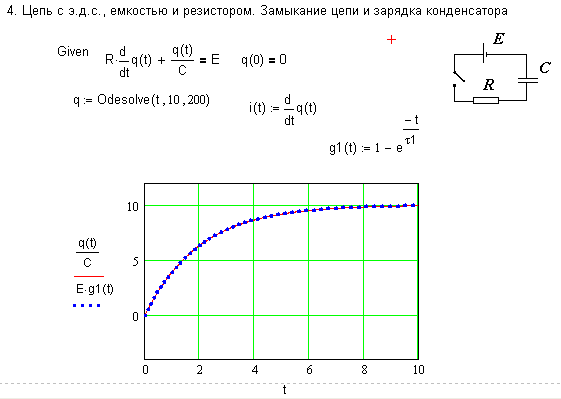
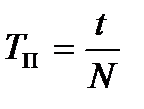 , (4.7)
, (4.7)