Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Главные напряжения при изгибеНаибольшее главное напряжение σ1 находится на верхних крайних волокнах и равно нулю на нижних крайних волокнах. Главное напряжение σ3 имеет наибольшее по абсолютной величине значение на нижних волокнах. Траектория главных напряжений зависит от типа нагрузки и способа закрепления балки.
Анализ напряженного состояния прямоугольного сечения
Анализ напряженного состояния при изгибе для балки двутаврового сечения При решении задач достаточно отдельно проверить нормальные и отдельно касательные напряжения. Однако иногда наиболее напряженными оказываются промежуточные волокна, в которых имеются и нормальные, и касательные напряжения. Это происходит в сечениях, где одновременно и изгибающий момент, и поперечная сила достигают больших значений — это может быть в заделке консольной балки, на опоре балки с консолью, в сечениях под сосредоточенной силой или в сечениях с резко меняющейся шириной. К примеру, в двутавровом сечении наиболее опасны места примыкания стенки к полке — там имеются значительные и нормальные, и касательные напряжения. Сдвиг. Кручение прямого стержня Чистый сдвиг. Закон Гука при сдвиге. Модуль сдвига. Условие прочности при кручении с учетом принятых обозначений формулируется следующим образом: максимальные касательные напряжения, возникающие в опасном сечении вала, не должны превышать допускаемых напряжений и записывается в виде
где  - из второй теории прочности
- из теории Мора
Из теорий прочности для пластичных материалов при чистом сдвиге получим: - по третьей теории прочности
- по четвертой теории прочности
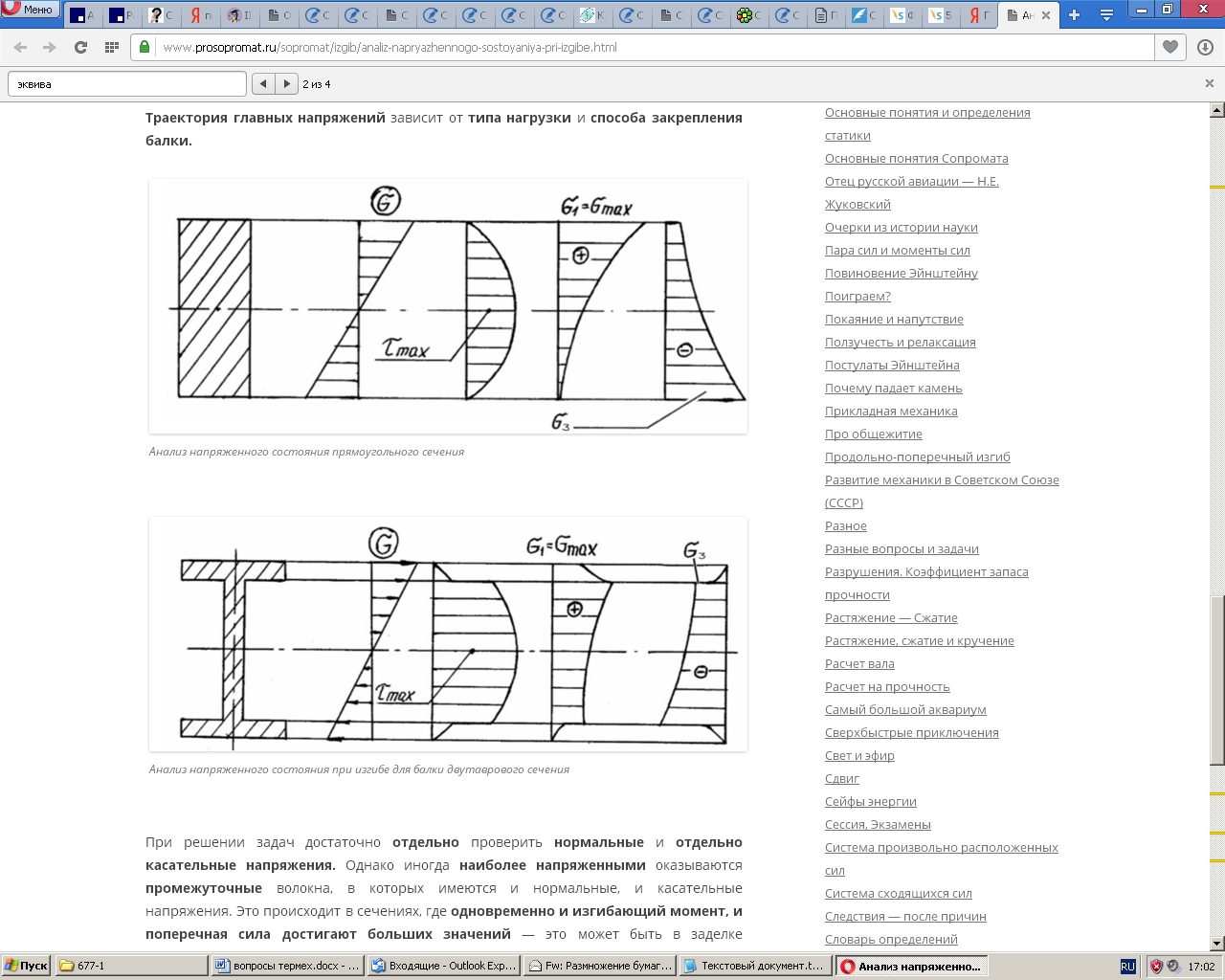
Как следует из закона парности касательных напряжений, одновременно с касательными напряжениями, действующими в плоскости поперечного сечения вала, имеют место касательные напряжения в продольных плоскостях. Они равны по величине парным напряжениям, но имеют противоположный знак. Таким образом, все элементы бруса при кручении находятся в состоянии чистого сдвига. Так как чистый сдвиг является частным случаем плоского напряженного состояния, при котором В пределах упругости касательное напряжение прямо пропорционально относительному сдвигу
– это закон Гука при сдвиге; G – модуль сдвига, Н/м2, характеризующий жесткость материала при сдвиге. Закон Гука при сдвиге через абсолютные деформации:
где а – расстояние между сдвигаемыми гранями; А – площадь грани. Модуль сдвига G, модуль продольной упругости Е и коэффициент Пуассона
Удельная потенциальная энергия деформации сдвига равна
На практике чаще всего теория сдвига применяется к расчету болтов, заклепок, шпонок, сварных швов и других элементов соединений. |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 574. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 - берется либо на основании опытных данных, либо (при отсутствии нужных опытных характеристик) по теориям прочности, соответствующим материалу. Например, из теорий прочности для хрупких материалов, примененных для чистого сдвига, следуют такие результаты:
- берется либо на основании опытных данных, либо (при отсутствии нужных опытных характеристик) по теориям прочности, соответствующим материалу. Например, из теорий прочности для хрупких материалов, примененных для чистого сдвига, следуют такие результаты:




 , то при повороте граней элемента на 450 в новых площадках обнаруживаются только нормальные напряжения, равные по величине
, то при повороте граней элемента на 450 в новых площадках обнаруживаются только нормальные напряжения, равные по величине 

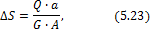
 материала связаны зависимостью
материала связаны зависимостью