
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Экспериментальное получение ВАХВольтамперные характеристики НЭ могут быть получены экспериментально. Для этого собирают электрическую цепь по одной из двух схем, показанных на рис. 11.3, а, б.
При этом следует иметь в виду, что измерительные приборы обладают сопротивлениями, указанными на их лицевой стороне. Сопротивления амперметра RA и вольтметра RV могут быть соизмеримы с сопротивлениями НЭ, поэтому при снятии ВАХ следует производить перерасчет данных для построения характеристик. Так, при снятии ВАХ по схеме рис. 11.3, а следует учесть, что вольтметр покажет суммарное напряжение амперметра и нелинейного элемента Поэтому при заданных значениях тока напряжение на НЭ определяют по формуле и только после этого строят вольтамперную характеристику. В случае, если сопротивление нелинейного элемента намного больше сопротивления амперметра, то напряжением амперметра можно пренебречь и считать, что При снятии ВАХ по схеме рис. 11.3, б получают погрешность вследствие того, что амперметр измеряет суммарный ток Поэтому при заданных значениях напряжения определяют ток НЭ по формуле после чего строят зависимость IНЭ(U). В случае, если сопротивление нелинейного элемента намного меньше сопротивления вольтметра, то током вольтметра можно пренебречь и считать, что Полученные экспериментальным способом вольт-амперные характеристики НЭ используют далее для описания свойств НЭ и для расчета электрической цепи, содержащей нелинейные элементы. Статическое и динамическое сопротивления НЭ
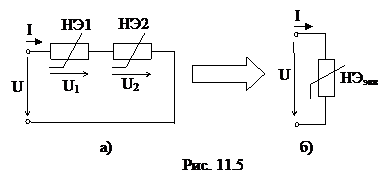
 Статическим сопротивлением RСТ нелинейного элемента в заданной точке а его характеристики называют отношение напряжения на НЭ к току в нем. Из рис. 11.4 видно, что это сопротивление пропорционально тангенсу угла α, образованного прямой, соединяющей точку а с началом координат, и осью токов: где mU, mI, mR – соответственно масштабы осей напряжения, тока, сопротивления. Дифференциальным или динамическимсопротивлением Rдиф нэ в заданной точке а его характеристики называют производную от напряжения по току. Это сопротивление пропорционально тангенсу угла β между касательной к ВАХ в точке а и осью токов (рис. 11.4): Для участка ВАХ дифференциальное сопротивление равно отношению конечного приращения напряжения к конечному приращению тока: Если рабочая точка а находится на падающем участке ВАХ, то дифференциальное сопротивление в таком случае будет отрицательным. Графический метод расчета нелинейных цепей Постоянного тока Нелинейные цепи простой конфигурации удобно рассчитывать графическим методом. Рассмотрим графический метод расчета нелинейных цепей с последовательным, параллельным и смешанным соединением нелинейных элементов. Последовательное соединение НЭ. На рис. 11.5, а показано последовательное соединение двух НЭ, вольтамперные характеристики которых I(U1) и I(U2) представлены на рис. 11.6 (кривые 1 и 2 соответственно).
Эти два элемента можно заменить одним эквивалентным (рис. 11.5, б) с вольтамперной характеристикой I(U), построенной на рис. 11.6 (кривая 3). Построение каждой точки этой характеристики выполняется на основании уравнения, записанного по второму закону Кирхгофа для цепи рис. 11.5, а Задаваясь значением тока I', по ВАХ (рис. 11.6) определяют напряжения U'1 и U'2 на нелинейных элементах (кривые 1 и 2) и рассчитывают напряжение U' в соответствии со вторым законом Кирхгофа По координатам U' и I' получают точку суммарной ВАХ (кривая 3 рис. 11.6). Все остальные точки характеристики эквивалентного нелинейного элемента строят аналогичным образом.
Полученная характеристика I(U) (кривая 3 рис. 11.6) позволяет определить ток I цепи для любого заданного значения входного напряжения U (рис. 11.7). А по значению этого тока определить напряжения на НЭ U1 и U2 по вольтамперным характеристикам этих элементов. Для расчета цепи (рис. 11.8), где одним из элементов является линейный резистор с сопротивлением R, графические построения можно провести и другим методом - методом пересечения характеристик.
Согласно второму закону Кирхгофа записывают Полученное уравнение решают графически. Для этого на координатной плоскости строят ВАХ нелинейного элемента Как показано на рис. 11.9, прямая MN соответствует линейному уравнению и построена по двум точкам, соответствующим режиму холостого хода (I=0, Uлхх=U) и режиму короткого замыкания (Uл=0, I=IК= Графическим решением уравнения Параллельное соединение нелинейных элементов показано на рис. 11.10, а. Характеристики этих НЭ I1(U) и I2(U) представлены на рис. 11.11 (кривые 1 и 2 соответственно).
Эти два элемента можно заменить одним эквивалентным (рис. 11.10, б) с вольт-амперной характеристикой I(U), изображенной на рис. 11.11 – кривая 3. Для этого задаются произвольными значениями напряжения и суммируют соответствующие ординаты характеристик НЭ, то есть графически реализуют первый закон Кирхгофа: I(U)=I1(U)+I2(U).
Результирующая характеристика параллельно соединенных нелинейных элементов используется в том случае, если по заданному току I требуется определить напряжение U на зажимах цепи, а также при расчете цепей при смешанном соединении элементов. Смешанное соединение НЭ. На рис. 11.12, а показана схема смешанного соединения НЭ, а на рис 11.12, б приведены их ВАХ I1(U1), I2(U2), I3(U2) - кривые 1, 2 и 3 соответственно.
Графическое построение для определения токов и напряжений приведено на рис. 11.12, б. Сначала производим замену двух параллельно соединенных элементов одним эквивалентным с характеристикой I1(U2)=(I2+I3)(U2) (кривая 4). Затем строим вольт-амперную характеристику всей цепи (кривая 5 рис. 11.12, б) U(I1) = U1(I1) + U2(I1)= U1(I1) + U2(I2+ I3). Для этого, задаваясь произвольными значениями тока I1, суммируют соответствующие абсциссы кривых 4 и 1. Далее, на оси абсцисс откладываем заданное напряжение U и проводим прямую, параллельную оси ординат, до пересечения с кривой I1(U) и на оси ординат находим ток I1, соответствующий заданному напряжению. При этом значении тока по кривой I1(U2) находим напряжение U2, а по кривой I1(U1) –значение напряжения U1. По найденному значению напряжения U2 на кривых I2(U2) и I3(U2) находим токи параллельных ветвей I2 и I3.
Стабилизатор напряжения Стабилизатором напряжения называют устройство, поддерживающее с определенной точностью неизменным напряжение на нагрузке. Изменение напряжения на нагрузке может быть вызвано рядом причин: колебаниями напряжения первичного источника питания (сети переменного напряжения, аккумулятора, гальванического элемента), изменением нагрузки, изменением температуры окружающей среды и др.
С помощью такого стабилизатора можно получить стабилизированное напряжение от нескольких вольт до нескольких сотен вольт при токах от единиц миллиампер до нескольких ампер. Стабилитрон в параметрическом стабилизаторе включают параллельно нагрузочному резистору Rн (рис. 11.13). Последовательно со стабилитроном для создания требуемого режима работы включают балластный резистор Rб. При увеличении входного напряжения увеличивается ток стабилитрона. В результате увеличивается напряжение на балластном резисторе Rб, а выходное напряжение, согласно второму закону Кирхгофа, остается неизменным
и найти значения тока стабилитрона При увеличении входного напряжения Для нормальной работы параметрического стабилизатора сопротивление балластного резистора Rб должно быть таким, чтобы его ВАХ пересекала ВАХ стабилитрона в точке А, соответствующей номинальному току стабилитрона Основным коэффициентом, характеризующим работу стабилизатора, является коэффициент стабилизации по напряжению КстU. Коэффициент стабилизации есть отношение относительного изменения выходного напряжения
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 971. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 .
.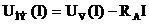
 .
. .
.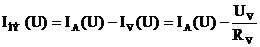 ,
,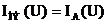 .
. При расчете нелинейных цепей помимо ВАХ используют также некоторые числовые параметры, например статическое и динамическое сопротивления нелинейного элемента.
При расчете нелинейных цепей помимо ВАХ используют также некоторые числовые параметры, например статическое и динамическое сопротивления нелинейного элемента. ,
, .
.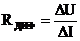 .
.
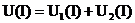 .
.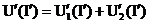 .
.

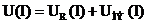 или
или 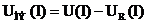 .
.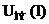 - кривая 1 рис. 11.9 и ВАХ линейной части схемы
- кривая 1 рис. 11.9 и ВАХ линейной части схемы 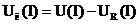 - прямая 2, проходящая через точки M и N.
- прямая 2, проходящая через точки M и N. ) на участке цепи с НЭ.
) на участке цепи с НЭ.
 Для нахождения токов в параллельно соединенных НЭ, в случае если известно входное напряжение, построение результирующей характеристики не требуется, так как токи находятся непосредственно по характеристикам НЭ.
Для нахождения токов в параллельно соединенных НЭ, в случае если известно входное напряжение, построение результирующей характеристики не требуется, так как токи находятся непосредственно по характеристикам НЭ.
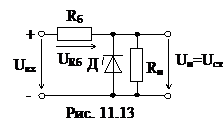 Для стабилизации напряжения в параметрических стабилизаторах напряжения при помощи стабилитрона (рис. 11.13) используют обратную ветвь вольт-амперной характеристики полупроводникового стабилитрона (рис. 11.14).
Для стабилизации напряжения в параметрических стабилизаторах напряжения при помощи стабилитрона (рис. 11.13) используют обратную ветвь вольт-амперной характеристики полупроводникового стабилитрона (рис. 11.14).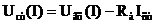 .
. Принцип действия параметрического стабилизатора удобно проиллюстрировать с помощью ВАХ стабилитрона, на которой построена опрокинутая вольт-амперная характеристика резистора Rб (прямые 1 и 2 рис. 11.14). Такое построение позволяет графически решить уравнение электрического состояния стабилизатора напряжения
Принцип действия параметрического стабилизатора удобно проиллюстрировать с помощью ВАХ стабилитрона, на которой построена опрокинутая вольт-амперная характеристика резистора Rб (прямые 1 и 2 рис. 11.14). Такое построение позволяет графически решить уравнение электрического состояния стабилизатора напряжения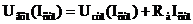
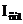 и выходного напряжения, т.е. напряжения на нагрузке стабилизатора
и выходного напряжения, т.е. напряжения на нагрузке стабилизатора  , которые соответствуют входному значению напряжения
, которые соответствуют входному значению напряжения  (прямая 1).
(прямая 1).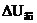 , например, из-за повышения напряжения сети, ВАХ балластного резистора Rб (прямая 1) переместится параллельно самой себе и займет положение 2. Из рис. 11.14 видно, что при этом напряжение
, например, из-за повышения напряжения сети, ВАХ балластного резистора Rб (прямая 1) переместится параллельно самой себе и займет положение 2. Из рис. 11.14 видно, что при этом напряжение  мало отличается от напряжения
мало отличается от напряжения  , т.е. практически напряжение на стабилитроне и на нагрузочном резисторе остается неизменным. Напряжение на нагрузочном устройстве остается неизменным также при снижении входного напряжения и изменении тока нагрузки
, т.е. практически напряжение на стабилитроне и на нагрузочном резисторе остается неизменным. Напряжение на нагрузочном устройстве остается неизменным также при снижении входного напряжения и изменении тока нагрузки 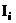 .
.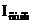 , значение которого указано в его паспортных данных. Диапазон изменения тока стабилитрона должен лежать в пределах от Iст.min до Iст.max, также указанных в паспортных данных.
, значение которого указано в его паспортных данных. Диапазон изменения тока стабилитрона должен лежать в пределах от Iст.min до Iст.max, также указанных в паспортных данных. к вызвавшему его относительному изменению входного напряжения
к вызвавшему его относительному изменению входного напряжения 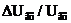 ,
,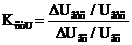 .
.