
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Соединенными резистором и конденсатором
Рассмотрим переходный процесс при включении цепи RC к источнику постоянного напряжения (рис. 9.4).
В соответствии со вторым законом Кирхгофа составим уравнение электрического состояния для рассматриваемой цепи относительно напряжения конденсатора: или с учетом того, что Решение этого дифференциального уравнения находится как сумма принужденной и свободной составляющих: uС(t) = uСпр(t) +uСсв(t) = U+ Вept . Характеристическое уравнение для этой схемы: RCp + 1=0, корень этого уравнения p = -1/(RC). Постоянная времени переходного процесса Постоянную интегрирования В найдем, рассмотрев искомую функцию в момент времени t=0. Так как схема до коммутации была отключена от источника питания, то есть конденсатор не был заряжен, то согласно второму закону коммутации начальное значение напряжения на конденсаторе uС(0+) = uС(0-) = 0. Так как uС(0+)= U + B =0, то В = uc(0+) – U = –U. Искомая переходная функция имеет вид Ток в цепи
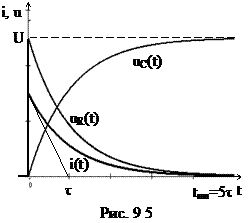
Графики переходных функций тока и напряжений представлены на рис. 9.5.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 580. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 После замыкания ключа происходит процесс заряда конденсатора до величины напряжения U источника питания. В течение этого времени в цепи протекает ток, который после полной зарядки конденсатора становится равным нулю. Это физическое понимание переходного процесса. Опишем процесс математически.
После замыкания ключа происходит процесс заряда конденсатора до величины напряжения U источника питания. В течение этого времени в цепи протекает ток, который после полной зарядки конденсатора становится равным нулю. Это физическое понимание переходного процесса. Опишем процесс математически.

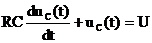 .
.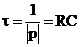 .
.
 .
. Напряжение на резистивном элементе
Напряжение на резистивном элементе