
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
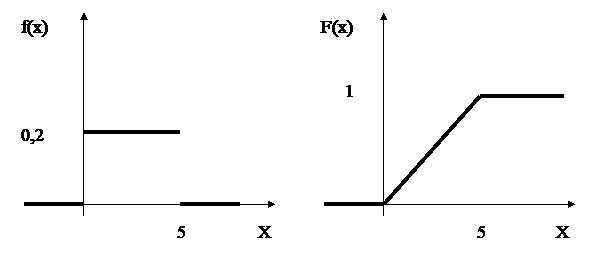
Непрерывная случайная величина. ⇐ ПредыдущаяСтр 5 из 5 Пример 1: Непрерывная случайная величина Х задана функцией распределения: Требуется: а) найти функцию плотности распределения f(x); б) найти математическое ожидание М(Х), дисперсию D(Х) и среднее квадратическое отклонение σ (Х); в) построить графики функций f(x) и F(x); г) найти P(–1 < Х < 1). Решение: а) по определению функции плотности вероятности f(x) = F¢ (x) , тогда
б) для непрерывной случайной величины
D(X) = M(Х2) - [M (Х)]2 = 2 -
г) для вычисления вероятности попадания непрерывной случайной величины в интервал (α ,β) можно применить одну из формул:
Применим первую формулу P (–1 < Х < 1) = F(1) – F(–1) = Пример 2. Случайная величина Х задана плотностью распределения: Требуется: а) найти коэффициент С; б) функцию распределения F(x); Решение: а) плотность распределения f(x) должна удовлетворять условиям:
Тогда
Так как Таким образом, б) для нахождения функции распределения F(x) воспользуемся формулой
Если х ≤ 1 , f(x) = 0, то
Если 1 < х ≤ 5,
Если х > 1,
Итак ,
Законы распределения непрерывных случайных величин
Равномерное распределение Непрерывная случайная величина Х распределена равномерно на отрезке [а, b], если на этом интервале её функция плотности имеет вид
Функция распределения для равномерного закона
Математическое ожидание и дисперсия вычисляются по формулам  М(Х) = Пример 1. Поезда метро идут строго по расписанию. Интервал движения – 5 минут. Составить f(х) и F(х) случайной величины Х – времени ожидания очередного поезда и построить их графики. Найти М(Х), D(Х). Решение: Случайная величина Х – время ожидания очередного поезда. Величина Х распределена равномерно на отрезке [0,5], поэтому
М(Х) = Нормальное распределение Закон нормального распределения должен быть изучен наиболее основательно, т.к. он часто применяется в теории и практике. Непрерывная случайная величина Х распределена по нормальному закону, если её плотность распределения вероятностей выражается формулой f(х) = Параметры а и σ имеют следующий вероятностный смысл: а = М(Х), σ 2= D(Х), σ = График плотности нормального распределения называют нормальной кривой (кривой Гаусса). Функция ƒ(х) определена на всей оси Х. При любых значениях Х функция принимает положительные значения, т.е. лежит выше оси ОХ. Точка (а, Точки перегиба (а-σ, Y
Если функция Лапласа задаётся формулой Ф(х) = Р ( a < Х < b) = Ф Р( Пример 2. Детали, выпускаемые цехом, по размеру диаметра распределены по нормальному закону. Стандартная длина диаметра детали равна а = 35, среднее квадратическое отклонение σ = 4. Требуется: а) составить функцию плотности вероятностей; б) найти вероятность того, что диаметр наудачу взятой детали будет больше a =34 и меньше b = 40; в) найти вероятность того, что диаметр детали отклонится от стандартной длины не более чем на e = 2. а) f(х) = б) Р(34 < Х < 40 ) = Ф = 0,3944 + 0,0987 = 0,4931; в) Р (
ТЕМА 6. ВЫБОРОЧНЫЙ МЕТОД
Проведение экономических исследований связано с изучением свойств различных совокупностей однотипных объектов (людей, предприятий, товаров и т.п.). При этом каждый объект, входящий в состав совокупности, характеризуется некоторым числом — величиной изучаемого признака X. Для обозначения таких совокупностей вводится понятие генеральной совокупности. Под генеральной совокупностьюпонимается вся совокупность однотипных объектов, которые изучаются в данном исследовании. Однако на практике в большинстве случаев мы имеем дело только с частью возможных наблюдений, взятых из генеральной совокупности. Выборка (выборочная совокупность) —это совокупность случайно отобранных объектов, составляющих лишь часть генеральной совокупности. Объёмом совокупности (выборочной или генеральной) называют число объектов этой совокупности. Например, из 1 000 изделий отобрано для обследования 100 изделий, объем генеральной совокупности N=1 000, а объём выборки n=100. В зависимости от способов отбора объектов из генеральной совокупности различают несколько типов выборок. Их типы, определения, свойства, примеры использования рекомендуется изучить самостоятельно. Пусть из генеральной совокупности извлечена выборка, причём х1 наблюдалось n1 раз, x2 – n2 раз,..., хk – nk раз и Статистическим распределением выборки называют перечень вариант xi и соответствующих им частот ni или относительных частот wi (причем сумма всех частот равна объёму выборки, а сумма всех относительных частот равна 1).
или
Вариационный ряд, заданный в таком виде, называют дискретным. Геометрической характеристикой дискретного вариационного ряда является полигон частот. Полигоном частот называют ломаную, отрезки которой соединяют точки (х1,n1), (х2,n2), …, (хk,nk), где хi — варианты выборки, а ni — соответствующие им частоты. Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот. Для непрерывно распределённого признака весь интервал, в котором заключены все наблюдаемые значения признака, разбивают на ряд частичных интервалов длины h и находят ni — сумму частот вариант попавших в i-й интервал. Такое распределение называют интервальным вариационным рядом. Геометрической характеристикой интервального вариационного ряда является гистограмма частот. Гистограммой частот называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению Пример 1. Из большой группы предприятий одной из отраслей промышленности случайным образом отобрано 30, по которым получены показатели основных фондов в млн руб.: 3; 4; 2; 3; 3; 6; 5; 2; 4; 7; 5; 5; 3; 4; 3; 2; 6; 7; 5; 4; 3; 4; 5; 7; 6; 2; 3; 6; 6; 4. Составить дискретное статистическое распределение выборки, записать распределение относительных частот, построить полигон частот. Решение. Различные значения признака запишем в порядке возрастания и под каждым из них запишем соответствующие частоты. Получим дискретное статистическое распределение выборки:
Проверка: сумма всех частот должна быть равна объёму выборки: n=4+7+6+5+5+3=30. Найдем относительные частоты, для чего разделим частоты на объём выборки
Напишем распределение относительных частот:
Контроль: Строим полигон частот. Для этого строим точки с координатами (xi;ni):(2;4), (3;7), (4;6), (5;5), (6;5), (7;3) и соединяем их последовательно отрезками.
Пример 2. Выборочно обследовано 26 предприятий лёгкой промышленности по объему валовой продукции. Получены следующие результаты в млн руб.: 15,0; 16,4; 17,8; 18,0; 18,4; 19,2; 19,8; 20,2; 20,6; 20,6; 20,6; 21,3; 21,4; 21,7; 22,0; 22,2; 22,3; 22,7; 23,0; 24,2; 24,2; 25,1; 25,3; 26,0; 26,5; 27,1. Составить интервальное распределение выборки с началом х0 = 15 и длиной частичного интервала h = 2,5. Построить гистограмму частот. Решение. Для составления интервального распределения составим таблицу. В первой строке расположим в порядке возрастания интервалы, длина каждого из которых h=2,5. Во второй сроке запишем количество значений признака в выборке, попавших в этот интервал (т.е. сумму частот вариант, попавших в соответствующий интервал).
Объём выборки n=2+5+10+4+5=26. Для построения гистограммы частот на оси абсцисс откладываем частичные интервалы на каждом из них строим прямоугольники высотой
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 239. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
. ;
; .
. .
. =
=  .
.

 .
. .
. .
. .
.

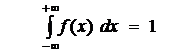 , следовательно
, следовательно  , следовательно С = 2.
, следовательно С = 2. ;
; .
.


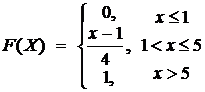 .
. .
.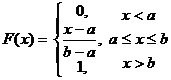 .
.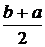 ; D(Х) =
; D(Х) =  .
. .
. 
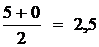 D(Х) =
D(Х) = 
 .
.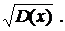
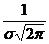 ) – точка max.
) – точка max.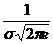 ) и (а+σ,
) и (а+σ,  ).
).

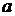
 X
X , то для нормально распределённой случайной величины
, то для нормально распределённой случайной величины – Ф
– Ф  .
. < e ) = 2Ф
< e ) = 2Ф  .
.  ;
;  - Ф
- Ф  = Ф (1,25) + Ф (0,25) =
= Ф (1,25) + Ф (0,25) = < 2 ) = 2Ф
< 2 ) = 2Ф  = 2Ф (0,5) = 0,3829.
= 2Ф (0,5) = 0,3829. –объём выборки. Наблюдаемые значения хi называют вариантами, а последовательность вариант, записанных в возрастающем порядке, — вариационным рядом. Числа наблюдений (ni) называют частотами, а их отношения к объёму выборки
–объём выборки. Наблюдаемые значения хi называют вариантами, а последовательность вариант, записанных в возрастающем порядке, — вариационным рядом. Числа наблюдений (ni) называют частотами, а их отношения к объёму выборки 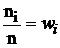 — относительными частотами.
— относительными частотами. .
. ;
; 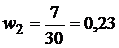 ;
; ;
; 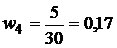 ;
;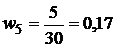 ;
;  .
. .
.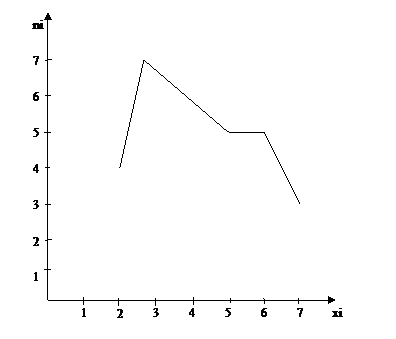




 10/2,5
10/2,5