Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Дискретная случайная величина
Пример 1. Дискретная случайная величина Х задана законом распределения:
Найти: а) математическое ожидание М(Х); б) дисперсию D(Х) и среднее квадратическое отклонение s (Х); в) составить функцию распределения F(х) и построить её график.
Решение: а) по формуле б) по формулам D(Х) = M (Х2) - [ M(Х)]2 и
D(Х) = 29,5 - (5,1)2 = 3,49 ; s(Х) = в) по определению F(x) = P(X < x ) , т.е. F(x) есть вероятность того, что случайная X примет значение меньше, чем х. Если х £ 2, то F(x) = P(X < 2) = 0. Если 2 < x £ 4, то F(x) = P(X < 4) = P(X=2) = 0,2. Если 4< x £ 5, то F(x) = P(Х < 5) = P(X=2)+(X=4) = 0,2+0,1 = 0,3. Если 5< x £ 7, то F(x) = P(Х<7)= P(X=2)+P(X=4)+P(X=5)=0,2+0,1+0,3 = 0,6. Если x>7, то F(x) = P(Х<7) = P(X=2) + P(X=4) + P(X=5) + P(X=7) = = 0,2+0,1+0,3+0,4 = 1. Построим график F(x):
Пример 2. В магазине куплено 3 электроприбора: чайник, утюг и пылесос. Вероятность выхода из строя в течение гарантийного срока для каждого из них соответственно равны р1=0,05, р2=0,1, р3 = 0,2. Составить закон распределения случайной величины Х – числа приборов, вышедших из строя в течение гарантийного срока. Решение: Х – число приборов, вышедших из строя, имеет следующие возможные значения: х1=0 – все три прибора не выйдут из строя в течение гарантийного срока; х2=1 – один прибор выйдет из строя; х3=2 – два прибора выйдут из строя; х4=3 – три прибора выйдут из строя. Найдём соответствующие этим значениям вероятности. По условию вероятности выхода из строя приборов равны:  р1=0,05; р2=0,1; р3=0,2, тогда вероятности того, что приборы будут рабочими в течение гарантийного срока равны: q1 = 1 – p1 = 1 – 0,05 = 0,95; q2 = 1 - p2 = 1 – 0,1 = 0,9; q3 = 1 – p3 = 1 – 0,2 = 0,8. P1 (X=0) = q1 ∙ q2 ∙ q3 = 0,95 ∙ 0,9 ∙ 0,8 = 0,684. P2 (X=1) = q1 ∙ q2 ∙ p3 + q1 ∙ p2 ∙ q3 + p1 ∙ q2 ∙ q3 = 0,95 ∙ 0,9 ∙ 0,2 + 0,95 ∙ 0,1 ∙ 0,8 + 0,05 ∙ 0,9 ∙ 0,8 = 0,283. P3 (X=2) = p1 ∙ p2 ∙ q3 + p1 ∙ q2 ∙ p3 + q1 ∙ p2 ∙ p3 = 0,05 ∙ 0,1 ∙ 0,8 + 0,05 ∙ 0,9 0,2 + 0,95 ∙ 0,1 ∙ 0,2 = 0,032. P4 (X=3) = p1 ∙ p2 ∙ p3 = 0,05 ∙ 0,1 ∙ 0,2 = 0,001. Проверка: P=P1(X=0)+P2(X=1)+P3(X=2)+P4(X=3)=0,684+0,283+0,032+0,001= 1 Закон распределения имеет вид:
Пример 3. Предприятие выпускает 90% изделий высшего сорта. Составить закон распределения случайной величины Х – числа изделий высшего сорта из трёх, взятых наудачу изделий. Найти M(X), D(X), s(Х). Решение: Случайная величина Х – число изделий высшего сорта среди трёх отобранных изделий может принимать одно из значений: 0, 1, 2, 3. Вероятности этих значений вычисляются по формуле Бернулли: Pn(X=m) = Cnm pm qn-m , такое распределение называют биноминальным. Известно, что n = 3 ; p = 0,9; q = 0,1; m = 0,1,2,3, тогда P1(X=0) = (0,1)3 = 0,001. P2(X=1) = C31 ∙ 0,91 ∙ 0,12 = 0,027. P3(X=2) = C32 ∙ 0,92 ∙ 0,1 = 0,243. P4(X=3) = 0,93 = 0,729. Проверка: Р= Р3(Х=0)+Р3(Х=1)+Р3(Х=2)+Р3(Х=3)= 0,001+0,027+0,243 +0,729 = 1. Закон распределения случайной величины Х:
M(X), D(X), s (X) случайной величины, распределённой по биноминальному закону, находятся по формулам: M(X) = np , D(X) = npq , s (X) = M(X) = 3 ∙ 0,9 = 2,7; D(X) = 3 ∙ 0,9 ∙ 0,1 = 0,27; s (X) = Пример 4. На сборку поступило 30 деталей, из них 25 стандартных. Сборщик берёт наудачу 3 детали. Составить закон распределения случайной величины Х – числа стандартных деталей среди трёх отобранных. Решение: Возможные значения случайной величины Х: Х1 = 0, Х2 = 1, Х3 = 2, Х4 = 3. Вероятности этих значений вычисляются по формуле Рn(Х=m) = где n – число элементов множества, s – число элементов множества, обладающих фиксированным свойством; r – число отобранных элементов; m= P3(X = 0) = P3(X = 2) = Проверка: Р = Р3(Х = 0)+Р3(Х = 1)+Р3(Х = 2)+Р3(Х = 3) = Закон распределения случайной величины Х:
Пример 5: Независимые случайные величины Х и У заданы законами распределения:
а) найти P(X=3), P(Y=3); б) составить закон распределения случайной величины Z = X + Y. Найти M(Z), D(Z) и проверить выполнение свойств M (X+Y) = M(X) + M(Y); D(X+Y) = D(X) + D(Y); в) составить закон распределения V = X × Y. Найти M(V) и проверить выполнение свойства M(X × Y) = M(X) × M(Y). Решение: а) Так как P(X=1) + P(X=3) + P(X=4) = 1, P(Y=0) + P(Y=2) + P(Y=3) = 1, то P(X=3) = 1 – (0,1 + 0,6) = 0,3, P(Y=3) = 1 – (0,2 + 0,4) = 0,4. Запишем законы распределения случайных величин X и Y, с учётом их вероятностей:
б) суммой случайных величин X и Y называется случайная величина Z = X + Y, возможные значения которой равны суммам каждого возможного значения величины X с каждым возможным значением величины Y. Если X и Y независимы, то вероятности возможных значений Z = X + Y равны произведениям вероятностей слагаемых.
Одинаковые значения величины Z объединяем, складывая их вероятности. Закон распределения случайной величины Z будет иметь вид:
M(Z) = 1 · 0,02 + 3 ·0,1 + 4 · 0,16 + 5 · 0,12 + 6 · 0,36 + 7 · 0,24 = 5,24 Или М(Z) = M(X) + M(Y), где M(X) = 1 · 0,1 + 3 · 0,3 + 4 · 0,6 = 3,4 M(Y) = 0 · 0,2 + 2 · 0,4 + 3 · 0,4 = 2 Тогда M(Z) = 3,4 + 2 = 5,4 Вычислим дисперсию случайной величины Z по формуле D(Z) = M(Z2) – [ M(Z)]2, где M(Z2) = 1 · 0,02+9 · 0,1+16 · 0,16 +25 · 0,12+36 · 0,36+43 · 0,24 = 31,2. Тогда D(Z) = 31,2 – (5,4)2 = 2,04. Или D(Z) = D(X) + D(Y), где D(X) = 1 ∙ 0,1 + 9 ∙ 0,3 + 16 ∙ 0,6 – (3,4)2 = 0,84 D(Y) = 0,2 ∙ + 4 ∙ 0,4 + 9 ∙ 0,4 – (2)2 = 1,2 Таким образом D(Z) = 0,84 + 1,2 = 2,04; в) составим закон распределения V = X ·Y. Произведением случайных величин X и Y называется случайная величина V = X · Y , возможные значения которой равны произведениям каждого возможного значения X на каждое возможное значение Y . Если X и Y независимы, то вероятности возможных значений V = X · Y равны произведениям вероятностей сомножителей.
Одинаковые значения величины V = X · Y объединяем, складывая их вероятности. Закон распределения V = X ·Y записываем так:
Найдём M(V) = 0 · 0,2 + 2 · 0,04 + 3 · 0,04 + 6 · 0,12 + 8 · 0,24 + 9 · 0,12 + 12·0,24 = 6,8. Или М(V) = M(X) ∙ M(Y) = 3,4 ∙ 2 = 6,8.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 173. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 находим математическое ожидание Х: М(Х) = 2 × 0,2 + 4 × 0,1 + 5 × 0,3 + 7 × 0,4 = 5,1;
находим математическое ожидание Х: М(Х) = 2 × 0,2 + 4 × 0,1 + 5 × 0,3 + 7 × 0,4 = 5,1; найдем дисперсию и среднее квадратическое отклонение.
найдем дисперсию и среднее квадратическое отклонение. = 22 × 0,2 + 42 × 0,1 + 52 × 0,3 + 72 × 0,4 = 29,5.
= 22 × 0,2 + 42 × 0,1 + 52 × 0,3 + 72 × 0,4 = 29,5. = 1,87;
= 1,87;
 .
. = 0,53.
= 0,53.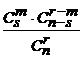 ,
, – число элементов с фиксированным свойством, оказавшихся в выборке. Такое распределение называют гипергеометрическим.
– число элементов с фиксированным свойством, оказавшихся в выборке. Такое распределение называют гипергеометрическим. . P3(X = 1) =
. P3(X = 1) =  .
.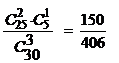 . P3(X = 3) =
. P3(X = 3) =  .
.