
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теорема умножения вероятностейПеред изучением данной темы студенту необходимо изучить следующий материал: зависимость и независимость событий, произведение событий, теоремы умножения зависимых и независимых событий, вероятность появления хотя бы одного события. Вероятность произведения двух событий вычисляется по формуле Р(А Р(А Пример 2. На станции отправления имеется 8 заказов на отправку товара: пять – внутри страны, а три – на экспорт. Какова вероятность того, что два выбранных наугад заказа окажутся предназначенными для потребления внутри страны? Решение. Событие А – первый взятый наугад заказ – внутри страны. Событие В – второй тоже предназначен для внутреннего потребления. Нам необходимо найти вероятность Р(А Р(А Пример 3. Из партии изделий товаровед наудачу отбирает изделия высшего сорта. Вероятность того, что выбранная вещь окажется высшего сорта равна 0,8; первого сорта – 0,7; второго сорта – 0,5. Найти вероятность того, что из трех наудачу отобранных изделий будут: а) только два высшего сорта; б) все разного сорта. Решение. Пусть событие А1 – изделие высшего сорта; событие А2 – изделие первого сорта; событие А3 – изделие второго сорта. По условию задачи Р(А1)=0,8, Р(А2)=0,7, Р(А3)=0,5. События А1,А2,А3 – независимы. 1. Событие А – только два изделия высшего сорта будет выглядеть так: А = А1А1А2 + А1А1А3, тогда Р(А) = Р(А1А1А2+А1А1А3) = Р(А1) + Р(А1) 2. Событие В – все три изделия различного сорта, выразим так  В= А1
ТЕМА 3. ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ. ФОРМУЛА БАЙЕСА
1. Формула полной вероятности Если событие А может произойти с одной из попарно несовместных гипотез Н1, Н2,….Нn, образующих полную группу, то вероятность появления события А равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А: P(A) = P(H1) × PH1(A) + P(H2) × PH2(A) + ….+ P(Hn) × PHn(A), где Пример 1. Фирма имеет три источника поставки комплектующих – фирмы А, В, С. На долю фирмы А приходится 50% общего объёма поставок, В – 30% и С–20%. Из практики известно, что 10% поставляемых фирмой А деталей – бракованные, фирмой В – 5% и С – 6%. Найти вероятность того, что наудачу выбранная деталь будет бракованной. Решение: Производится испытание: извлекается одна деталь. Событие А – появилась бракованная деталь. Гипотеза Н1 – деталь фирмы А. Гипотеза Н2 – деталь фирмы В. Гипотеза Н3 – деталь фирмы С. Тогда, согласно формуле полной вероятности, искомая вероятность равна P(A) = P(H1) Р(Н1) = Р(Н2) = Р(Н3) = Р(А) = 0,5
2. Формула Байеса Формула Байеса определяет условную вероятность появления гипотезы Hi, при условии, что событие А уже произошло:
Пример 2. В центральную бухгалтерию корпорации поступили пачки накладных для проверки и обработки. 90% пачек были признаны удовлетворительными: они содержали только 1% неправильно заполненных накладных. Остальные 10% пачек были признаны неудовлетворительными, так как содержали 5% неверно оформленных накладных. Взятая наугад из пачки накладная оказалась оформленной неверно. Учитывая это, какова вероятность того, что вся пачка накладных будет признана несоответствующей стандарту? Решение: Испытание: проверяется пачка накладных. Событие А – взятая наугад накладная оказалась неверной. Гипотеза Н1 – пачка не соответствует стандарту. Гипотеза Н2 – пачка соответствует стандарту. Необходимо узнать вероятность гипотезы Н1 при условии, что событие А произошло. Согласно формуле Байеса имеем:
Р(Н1) = Р(Н2) =
ТЕМА 4. ПОВТОРНЫЕ НЕЗАВИСИМЫЕ ИСПЫТАНИЯ
1. Формула Бернулли Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события А постоянна и равна р, событие А наступит ровно m раз, вычисляется по формуле Бернулли: Pn (m) = Cnm
Пример 1. Вероятность выигрыша по одному любому лотерейному билету равна 0,02. Чему равна вероятность выигрыша для владельца а) по трём билетам; б) не более двух билетов; в) хотя бы по одному билету; Решение: n = 4; p = 0,02 ; q = 0,98. a) P4 (3) = C43 б) P4 (0 ≤ m ≤ 2) = P4 (0) + P4 (1) + P4 (2) = C40 в) P4 (m ≥ 1) = 1 – P4 (0) = 1 – (0,98)4 = 0,078. 2. Локальная теорема Лапласа При большом числе испытаний для решения подобных задач применяется локальная формула Лапласа.
Функция φ (х) – чётная, т.е. φ(-х) = φ (х). Функция φ (х) табулированная на отрезке [0; 4], поэтому для х ≥ 4 функция φ (х) ≈ 0. В приложении 1 приведена таблица значений этой функции.
Пример 2. Доля изделий высшего сорта на данном предприятии составляет 90%. Найти вероятность того, что среди наудачу взятых 100 изделий высшего сорта окажется 84 изделия. Решение: n = 100; p = 0,9; q = 0,1; m = 84; n p = 90.
3. Теорема Пуассона Если вероятность p наступления события А в каждом испытании стремится к 0 (р→0) при неограниченном увеличении числа испытаний (n→∞), причём произведение n∙p стремится к постоянному числу λ = n∙p, то вероятность Рn(m) того, что событие А из n испытаний наступит m раз находится по формуле
В приложении 2 приведена таблица значений этой функции. Пример 3. Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Найти вероятность того, что магазин получит разбитых бутылок: а) ровно две; б) меньше двух; в) больше одной; г) хотя бы одну.
Решение: n = 1000; p = 0,003; λ = 1000 а) б) = 0,0498 + 0,1494 = 0,1992 ; в) P1000 (m>1) = 1 - P1000 (m ≤ 1) = 1 – [ P1000 (0) + P1000 (1)] = 0,8008 ; г) P1000 (m ≥ 1) = 1 - P1000 (0) = 1 – 0,0498 = 0,9502.
4. Интегральная теорема Лапласа Если вероятность р наступления события А в каждом из n независимых испытаний постоянна и отлична от 0 и 1, то при достаточно большом числе испытаний вероятность того, что событие наступает не менее m1 раз и не более m2 раз приближенно равна
где при х = 5 Ф(5) = 0,499 997 ≈ 0,5, поэтому для х > 5 полагают Ф(х) ≈ 0,5. Ф(х) нечётная, т.е. Ф(-х) = Ф(х).
Пример 4. Доля изделий высшего сорта продукции составляет 80%. Найти вероятность того, что в партии из 900 изделий высшего сорта будет: а) заключено между 700 и 750 ; б) не меньше 750; в) не больше 600. Решение. n = 900, р = 0,8, q = 0,2, n p = 720.
а) = Ф (2,5) + Ф (1,666) = 0,4938 + 0,4521 = 0,9459; б) = Ф(15) – Ф(2,5) = 0,5 – 0,4938 = 0,0062;
в) = Ф(-10) - Ф(-60) = -Ф(10) + Ф(60) = -0,5 + 0,5 = 0.
5. Наивероятнейшее число появления события Если n – число независимых испытаний, р – вероятность наступления события А в отдельном испытании, то наивероятнейшее число появления события А m0 удовлетворяет неравенству n
Пример 5. Предприятие поставляет свою продукцию 15 магазинам, от каждого из которых может поступить заявка на очередной день с вероятностью 0,6 независимо от заявок других магазинов. Найти наивероятнейшее число заявок. Решение: n = 15; p = 0,6; q = 0,4.
15
ТЕМА 5. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ИХ ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперёд неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определёнными вероятностями.
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка.
|
||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 210. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 В) = Р(А)
В) = Р(А) 
 =
= 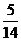 .
.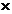 Р(А1)
Р(А1)  .
.








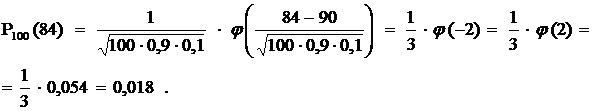
 .
.


 dt – функция Лапласа, или интеграл вероятностей. Таблица значений Ф(х) (приложение3) приводится для 0 ≤ х ≤ 5. Функция Ф(х) быстро возрастает и ограничена сверху:
dt – функция Лапласа, или интеграл вероятностей. Таблица значений Ф(х) (приложение3) приводится для 0 ≤ х ≤ 5. Функция Ф(х) быстро возрастает и ограничена сверху:


