
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Дисперсия альтернативного признака.Свой-ва дисперсии (матем.): 1.дисп-сия постоян-й вел-ны =0; 2.если все варианты значений признака уменьшились на одно и т.ж. число, то дисп-сия не уменьшится; 3.если все варианты значений признака уменьшить в одно и т.ж. число раз, то дисп-сия уменьшится в k² раз. Виды дисп-сий:-общая; межгруп-ая; внутригр-вая; альтернативного признака. Вариация, кот. обусловлена влиянием гру-го признака наз. межгруп-ой вариацией. Она измер-ся при помощи межгруп-й дисп-сии, кот. хар-зует изменение групп-х или частных ср-х по отношению к общ. ср. вел-не. S² =∑(Хi – Х)² fi \ ∑fi.Для опр-ия влияния всех факторов, кроме групп-го, вычисляют внутригруп. дисп-си, а затем опр-т ср. из внутригр-х дисп-сий - хар-зует вариацию результ-го признака, кот. возникает под влиянием всех остальных факторов, кроме групп-го. σi² = ∑(X - Xi)²fi\ fi.Ср. из внутригр-х дисп-сий вычисляется как ср. ариф.взвешен. Σi² =∑σi² - \ ∑, σ² = Ѕ²+σi².Общая дисп-сия оценивает влияние всех факторов на вариацию признака. Коэф. детерминации – отношение межгр-вой дисп-сии к общей. Он показывает долю вар-ции групп-го признака в общ. V вариаций признака. З² = Ѕ²/σ²*100%; З=√Ѕ²/σ² Корень кв. из коэф. детер-ции наз. эмпирическим корреляционнымотношением. Он хар-зует тесноту связи между групп-м и резул-м признаком. Показатели вар-ции применяются не только для оценки изменения колич-х признаков, но т.ж. для исслед-ия качест-х, альтернатив-х признаков. Альтернатив-й признак – признак, кот. имеет только 2 взаимозаключ. значения. 0 – отсутствие приз-ка; 1- наличие приз-ка; р – доля ед-ц, облад-щих данным приз-ком; q – доля ед-ц не облад-щих данным приз-ком. х = р; σ² = рq. 
№17.Виды дисперсий и правила сложения дисперсий. Дисперсия-(от лат. рассеивание)- это средний квадрат отклонений индивидуальных значений признака от общей средней: 1 18. Выб. наб. – вид стат набл., при котор. хар-ка всей совок. осущ. по отдел. части ед отобр. в случайн. порядке. Отобр. часть ед предст всю совок. 1)Ген. совок.-совок, из кот произв отбор. 2)Выбор. совок.-часть ед. генер. совок, кот. подлеж. непосредств. наблюд-ю.Содерж. выб. метода. включ. сист. правила. отбора ед и спос хар-ки изуч совок. Необход. заключ. в том, что он позвол. эконом. матер. и фин. рес, сокращ время на сбор и обраб. данных. Усл. примен :1)научно-обосн. спос. отбора ед 2) соблюд принципа беспрестр. отбора. Обоснование метода: по рез. этого наблюд. можно оценить изуч. параметры ген. совок. Задача выб. набл.-получить правильн. предст о показат. всей генер. совок. на осн. изучения выб. совок. Примен. 2 категор. обобщ. показ: относ вел. и средн. вел.
19. выбор набл-я по спос. отбора подразд. на след. виды:1.собств.-случ. выб-ка; 2. механич. выб-ка; 3.типич.---; 4.серийн.---; 5.комбинир.выб; 1- ед-цы совок-ти отбир-ся по жребию или по табл. случ. чисел. Эта выб. может осущ-ся 2-мя метадми: *повторн.; *бесповт; на практике более распростр. явл. бесповт. отбор.; 2- осущ-ся путем отбора ед-ц ч/з равн. интерв-лы. Велич. интерв-ла завис. от V-а генеральн. сов-ти. 2 всегда бесповт.; 3-предусм. Выдел-е типичн. групп по одн. признаку, кот. изуч-ся в выборочн. совок-ти. Из кажд. группы провод-ся случ. или механич. отбор ед-ц (м. б. пропорц. или непропорц.); 4-означ. что из генер. сов-ти отбир-ся не отдельн. ед-цы, а целые серии или партии. В кажд. серии провод. сплошн. набл-е.;5- основ-ся на сочит-и нескольк. способ. отбора. След. различ.: -многоступенч. -на кажд. стадии обслед-я ед-ца набл-я мен-ся.; -многофазов.-на кажд. стадии изуч-я ед-цы ост-ся прежними, но программа наблюд-я мен-ся.
20.Ошибки выб-ки зависят от следующих ф-ров:1от принятого спос-ба формир-я выборочной сов-ти; 2 от V выб-ки; 3от степени вариации признака. Различают средние и предельные ошибки выб-ки .Средние- ср. размер расхождений между обобщающими пок-лями выбор и генер-ной сов-ти.Если по одной и той же сов-ти неоднократно проводить выборочное набл-е,то вел-на изучаемого пр-ка будет измен-ся.Ср.размер расхождений изуч-го пр-ка будет оцениваться с помощью ср.ошибки выборки. Ср.ошибка опр-ся в 2 формах:1для измер-я ср. знач-я измер-го пр-ка µ=√σ²/n.2 для доли пр-ка:µ=√w*(1-w)/n, где w-доля ед. сов-ти, кот. обладает изуч. пр-к; n-кол-во ед.в выборочной сов-ти; σ-дисперсия. При бесповторном отборе: µ=√σ²/n*(1-n/N), где N-число ед. ген. сов-ти. µ=√ẁ(1-w)/n*(1-n/N). Ср. ошибки неразрывно связаны с предельной ошибкой выб-ки. Предельная ош-ка- возможно допустимые пределы колебаний изучаемого признака в изучаемой сов-ти. Она зависит от коэф-та доверия. В свою очередь коэф. доверия зависит от значения вероятности при кот. пров-ся выбор. наблюд-я. ∆-предельная ошика,t-коэф доверия; µ-ср. ошибка ∆=t*µ ∆х=t√σ²/n, ∆ẁ=t√ẁ(1-w)/n, при бесповторном:
∆x=t√σ²/n*(1-n/N),∆ẁ=t√W(1-W)/n*(1-n/N)Расчет предельной ошибки необходим для распр-я результатов выбор. наблюд-я на ошибки выб-ки всю ген. сов-ть. При изучении ср.знач-я пр-ка выбор.сов-ти довер. Интервалы ср. вел-ны ген. сов-ти опр-ся след. образом: х-∆х<=х<=х+∆х,где х-ср. вел. выор. сов-ти. W-∆ẁ<=P<=W+∆ẁ
|
||||||
|
Последнее изменение этой страницы: 2018-05-31; просмотров: 387. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
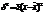 ; 2.
; 2. 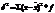 . Дисперсия не имеет размерности- это коэфф-т. Дисперсия обладает следующими математическими свойствами: 1.дисперсия постоянной величины=0; 2.если все варианты значений признака уменьшить на одно и тоже число, то дисперсия не уменьшится; 3.если все варианты значений признака уменьшить в одно и тоже число раз(k раз), то дисперсия уменьшится в
. Дисперсия не имеет размерности- это коэфф-т. Дисперсия обладает следующими математическими свойствами: 1.дисперсия постоянной величины=0; 2.если все варианты значений признака уменьшить на одно и тоже число, то дисперсия не уменьшится; 3.если все варианты значений признака уменьшить в одно и тоже число раз(k раз), то дисперсия уменьшится в  раз. Виды дисперсий:*общая, *межгрупповая, *внутригупповая, *дисперсия альтернативного признака. Показатели вариации применяются так же для определения тесноты связи между группировочными и результативными признаками. На вариацию признака влияют случайные и систематические причины. Для определения влияния какого-либо фактора на величину вариации признака используют аналитические группировки. Вариация, которая обусловлена влиянием группировочного признака наз.межгрупповой вариацией- она измеряется при помощи межгрупповой дисперсии(дисперсия групповых средних величин). Межгрупповая дисперсия характеризует изменение групповых или частных средних по отношению к общей средней величине, она определяется:
раз. Виды дисперсий:*общая, *межгрупповая, *внутригупповая, *дисперсия альтернативного признака. Показатели вариации применяются так же для определения тесноты связи между группировочными и результативными признаками. На вариацию признака влияют случайные и систематические причины. Для определения влияния какого-либо фактора на величину вариации признака используют аналитические группировки. Вариация, которая обусловлена влиянием группировочного признака наз.межгрупповой вариацией- она измеряется при помощи межгрупповой дисперсии(дисперсия групповых средних величин). Межгрупповая дисперсия характеризует изменение групповых или частных средних по отношению к общей средней величине, она определяется:  , где
, где  - средняя величина групповая,
- средняя величина групповая,  - сумма всех частот. Внутригрупповая дисперсия- для определения влияния всех факторов, кроме
- сумма всех частот. Внутригрупповая дисперсия- для определения влияния всех факторов, кроме  группировочного, вычисляют внутригрупповые дисперсии, а затем определяют среднюю из внутригрупповых дисперсий. Средняя из внутригрупповых дисперсий характеризует вариацию результативного признака, которая возникает под влиянием всех остальных факторов кроме группировочного. Внутригрупповые, или частные, дисперсии определяются по формуле:
группировочного, вычисляют внутригрупповые дисперсии, а затем определяют среднюю из внутригрупповых дисперсий. Средняя из внутригрупповых дисперсий характеризует вариацию результативного признака, которая возникает под влиянием всех остальных факторов кроме группировочного. Внутригрупповые, или частные, дисперсии определяются по формуле:  =∑ (х -
=∑ (х - 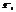 )
) 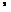 * f
* f  / f
/ f  .В математической статистике доказано, что общая дисперсия признака равна сумме межгрупповой и ср. арифм. внутригрупповых дисперсий:
.В математической статистике доказано, что общая дисперсия признака равна сумме межгрупповой и ср. арифм. внутригрупповых дисперсий:  .Отношение межгрупповой дисперсии к общей дает коэф-т детерминации
.Отношение межгрупповой дисперсии к общей дает коэф-т детерминации  , характеризующий долю вариации группировочного признака в общем объеме вариации, или на сколько процентов уровень результативного признака определяется группировочным признаком. Этот показатель обычно выражается в процентах:
, характеризующий долю вариации группировочного признака в общем объеме вариации, или на сколько процентов уровень результативного признака определяется группировочным признаком. Этот показатель обычно выражается в процентах:  . Корень квадратный из этого же отношения наз.эмпирическим корреляционным отношением(η). Он характеризует тесноту связи между признаками, т.е. близость корреляционной(неполной) зависимости к функциональной(полной).Этот показатель изменяется от 0 до 1.Точность его зависит от размеров совокупности, чем больше совокупность, тем он надежнее. К недостаткам эмпир. корреляц. отнош. относят невозможность определить направление связи (т.е. нельзя сказать, это прямая зависимость или обратная) и невозможность определения математической формы связи.
. Корень квадратный из этого же отношения наз.эмпирическим корреляционным отношением(η). Он характеризует тесноту связи между признаками, т.е. близость корреляционной(неполной) зависимости к функциональной(полной).Этот показатель изменяется от 0 до 1.Точность его зависит от размеров совокупности, чем больше совокупность, тем он надежнее. К недостаткам эмпир. корреляц. отнош. относят невозможность определить направление связи (т.е. нельзя сказать, это прямая зависимость или обратная) и невозможность определения математической формы связи.