
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ЧИСЛЕННЫЕ МЕТОДЫ ОПТИМИЗАЦИИ.В основу численных методов оптимизации положена идея целенаправленного формирования последовательности точек Центральным вопросом численной оптимизации является вопрос выбора подходящего вычислительного алгоритма и анализа его сходимости. Алгоритм поиска оптимального решения сходится, если он непосредственно вычисляет значение Во втором случае о сходимости можно говорить только в смысле существования Рассмотрим некоторые, наиболее использующиеся методы численной оптимизации. Методы возможных направлений. Идея метода возможных направлений проста: из начальной, допустимой по условиям задачи точки
где, Приведенное выражение является общим. Разница между методами заключается в способе задания 
Метод крутого восхождения (наискорейшего спуска). В основе метода крутого восхождения лежат следующие правила: 1. В качестве вектора возможных направлений выбирается вектор градиента целевой функции
2.Величина шага - либо из условия - либо задается фиксировано; - либо изменяется по определенному правилу (увеличивается, либо уменьшается) В указанном виде метод используется только тогда, когда отсутствуют ограничения на переменные. Если функция Если целевая функция невыпуклая, то существует несколько точек экстремума функции и метод из разных начальных точек может сходиться к разным локальным экстремальным точкам. В качестве критерия остановки(близости к
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 278. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,
,  ,
,  ,… в области
,… в области 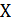 определения целевой функцией
определения целевой функцией  т.о., чтобы обеспечить движение к оптимальному решению
т.о., чтобы обеспечить движение к оптимальному решению  . При этом каждый из шагов дает некоторую информацию о направлении движения в сторону оптимума, величине шага и т.д.
. При этом каждый из шагов дает некоторую информацию о направлении движения в сторону оптимума, величине шага и т.д. за конечное число шагов, либо представляет его в виде ее предельного значения
за конечное число шагов, либо представляет его в виде ее предельного значения 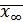 последовательности точек
последовательности точек  ,в которой значение целевой функции z лучше, чем в предыдущей. И так до тех пор, пока есть возможность улучшения z. Каждый шаг основан на выборе подходящего направления движения из очередной точки
,в которой значение целевой функции z лучше, чем в предыдущей. И так до тех пор, пока есть возможность улучшения z. Каждый шаг основан на выборе подходящего направления движения из очередной точки  и оценке требуемой «длины шага» таким образом, что позволяет в итоге найти
и оценке требуемой «длины шага» таким образом, что позволяет в итоге найти  =
= 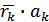 ,
, -величина k-ого шага ;
-величина k-ого шага ;  -единичный вектор ,определяющий направление перемещения.
-единичный вектор ,определяющий направление перемещения. , т.е.
, т.е. =
= 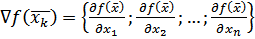
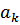 определяется
определяется  ,
,
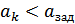 , то останов), либо приращение целевой функции
, то останов), либо приращение целевой функции  (если
(если  , либо максимальное число шагов
, либо максимальное число шагов  , либо их все в совокупности. Все эти способы оценки сходимости к оптимальному решению имеют свои недостатки и не позволяют полностью оценить близость найденного решения к оптимальному.
, либо их все в совокупности. Все эти способы оценки сходимости к оптимальному решению имеют свои недостатки и не позволяют полностью оценить близость найденного решения к оптимальному.