
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Метод покоординатного подъема (спуска).В этом случае в качестве возможного направления движения поочередно выбирают движение вдоль одной из координатных осей, начиная, например, с Обычно Максимизировать по переменной xi целевую функцию f(x1,…,xn), где все
После этого осуществляется движение по следующей переменной xi+1 , фиксируя все остальные и так до последней - xn. Затем происходит возврат к первой переменной x1 и процесс (цикл) повторяется снова. Метод сходится в случае выпуклой целевой функции. В качестве критерия остановки обычно используют величину приращения целевой функции от цикла к циклу
Если
Сходимость приведенных методов основана на выпуклости целевой функции и отсутствии ограничений. В случае нарушения этих условий необходимо использовать другие методы оптимизации (см. литературу).
Решение задачи нелинейного программирования существенно усложняется, если множество возможных значений переменных Х – дискретное. В некоторых случаях применимы методы, вытекающие из вида целевой функции и специфики задачи. Однако их применение в других задачах невозможно (например, разностные методы и метод динамического программирования в задачах распределения ресурсов с аддитивной целевой функцией). При невысокой размерности задачи (число вариантов решений сравнительно невелико) могут быть использованы методы прямого перебора. Однако, когда число переменных велико они становятся практически неприменимы (см. литературу).  ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ.
Модели и методы. В широком смысле под имитационным моделированием понимается моделирование тех или иных процессов функционирования исследуемых систем путем их имитации ( подражания ). В соответствии с этим под имитационными моделями можно понимать любые модели, отражающие связь между показателями функционирования системы и параметрами, задающими ее характеристики, стратегии применения и условия функционирования. В общем случае сюда можно отнести: Аналитические модели – отражающие эту связь в виде аналитических выражений (формул, уравнений, неравенств и т.д. ) Численные модели – позволяющие определить показатели функционирования системы в результате численного решения уравнений, ее описывающих, если аналитическое решение их невозможно или нецелесообразно из-за высокой сложности задачи. В случаях, когда аналитические или численные модели не применимы, или необходимо проверить их адекватность с помощью более детальных моделей, используются имитационные модели. Под имитационной моделью будем понимать модель, в которой зависимости, отображающие связи между показателями эффективности системы и параметрами ее и внешней среды реализуется в виде некоторого моделирующего алгоритма, осуществляющего взаимосвязанное синхронизированное изменение переменных ее состояния таким же образом, как и в реальной системе в процессе ее функционирования. Выполнение этого алгоритма не дает решения модели. С помощью него лишь осуществляется единичная реализация аналога процесса функционирования или прогон модели, который является подобием экспериментов с реальной системой. В этом случае говорят, что проводится имитационный эксперимент на модели. Имитационные модели могут быть реализованы на аналогово-цифровых ЭВМ. Моделирование на АВМ обладает высоким быстродействием, но в то же время имеет невысокую точность. Кроме того на них не очень удобно задавать систему логических связей и ограничений, невозможна реализация дискретных процессов. Цифровые ЭВМ свободны от этих недостатков, хотя и обладают меньшим быстродействием при отображении динамических процессов, описывающих с помощью систем дифференциальных уравнений. В то же время они обладают неограниченными возможностями по моделированию дискретных процессов с учетом любых взаимосвязей, характерных для процессов функционирования современных сложных технических систем от отдельных станков и агрегатов до предприятий и отраслей. Поэтому имитационные модели наиболее широко реализуются на ЦВМ с помощью специальных разрабатывающих программ, реализующих моделирующий алгоритм. |
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 309. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
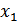 , фиксируя при этом значение всех остальных переменных
, фиксируя при этом значение всех остальных переменных 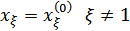 . Величину шага
. Величину шага  определяем из условия
определяем из условия  , где
, где  -единичный вектор движения по i-ой координате .
-единичный вектор движения по i-ой координате . находят решая задачу оптимизации :
находят решая задачу оптимизации : =
=  , ξ≠i, ξ=1,n. Ограничений на xi не накладывается.
, ξ≠i, ξ=1,n. Ограничений на xi не накладывается.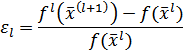
 <ε , то процесс заканчивается и принимается
<ε , то процесс заканчивается и принимается  . (см. рис.)
. (см. рис.)