
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Оценка сложных систем на основе теории полезности.При аксиоматическом подходе к оценке систем на основе теории полезности используется метод свертывания векторного критерия в скалярный. Отличие данного подхода от других состоит в том, что свертывание производится на основе аксиоматизации предпочтений ЛПР. Естественные отношения порядка на шкальных значениях критериев здесь не используются, так как все компоненты векторного критерия на основе предпочтений ЛПР преобразуются (в общем случае нелинейно) в функции полезности компонентов и лишь затем осуществляется свертывание. В теории полезности исходят из того, что критерий эффективности предназначен для выявления порядка предпочтений на альтернативах (исходах операции), что позволяет обеспечить обоснованный выбор решения. Выявить формально отношение предпочтения или безразличия непосредственным сравнением альтернатив затруднительно: показатели исходов операции многочисленны, имеют разный физический смысл и разные шкалы измерений (стоимость изготовления, численность обслуживающего персонала, коэффициент технической готовности, пропускная способность, вероятность вскрытия направления связи при передаче сообщений и т.п.). Было бы очень удобно иметь для оценки исходов какую-то единую меру что-то вроде денег. Однако деньги тоже не выступают универсальной мерой ценности. С помощью их не все можно оценивать (репутацию, настроение и т.д.). Кроме того, они обеспечивают измерение по равномерной шкале (100 руб. в пять раз ценнее, чем 20 руб.). Вместе с тем известно, что иногда ценность денежной суммы возрастает непропорционально ее величине. Поскольку в нашей практике нет универсальной меры, обладающей физическим смыслом и позволяющей соизмерить исходы операций по неравномерной шкале, а потребность в ней существует, то остается одно ввести какую-то искусственную меру. Такая мера определяется через полезность альтернатив (исходов). Большинство людей используют сравнительно простой подход к оценке альтернатив упорядочение их по возрастанию полезности от наименее полезных до наиболее полезных. Свое отношение к альтернативам люди могут выразить и количественно, приписав каждому исходу некоторое число, определяющее его относительную предпочтительность. Например, наименее полезный исход может быть отражен числом 1, следующий числом 2 и т.д., до наиболее полезного исхода. 
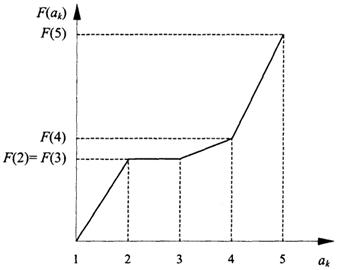
Зная возможные альтернативы с их показателями полезности, можно построить функцию полезности, которая дает основу для сравнения и выбора решений. Функция Рис. 2.8. Функция полезности полезности представляет собой числовую ограниченную функцию F(a), определенную на множестве альтернатив А = {ak}, k = 1, 2, ... ,l, так, что F(ai) = F(aj), когда альтернативы аi и аj неразличимы (аi∼аj), т.е. нельзя отдать предпочтение ни тому, ни другому исходу, и F(ai) >F(aj), когда альтернатива аi предпочтительнее альтернативы аj (аi Возникает вопрос, можно ли с математической точки зрения доказать существование функции полезности в виде отображения упорядоченного множества альтернатив А в множество действительных чисел φ: А → R1, обеспечив тем самым естественное упорядочение всех альтернатив. В теории полезности доказывается, что при вполне естественных допущениях относительно предпочтений ЛПР такая функция существует. Предпочтения ЛПР формулируются в виде аксиом. Поскольку системы предпочтений у разных ЛПР могут различаться, то разные аксиоматики приводят к различным видам свертки и, следовательно, функция полезности не единственна. Причина заключается в том, что отсутствуют определения нулевой полезности, единицы полезности и шкалы полезности (можно произвольно выбирать нуль, единицу и шкалы измерения полезности альтернатив). Рассмотрим основные аксиомы теории полезности. Аксиома 1. Измеримость. Каждому альтернативному исходу ai может быть поставлено в соответствие неотрицательное действительное число pi, рассматриваемое как мера относительной полезности исхода ai, i = 1, ... , n, 0 ≤ рi ≤ 1. Аксиома 2. Сравнимость. Любые два исхода (альтернативы) аi и аj сравнимы: либо один исход предпочтительнее другого, либо исходы одинаково предпочтительны (эквивалентны). Другими словами, при сравнении двух альтернатив аi и аj возможен один из трех выводов: предпочтительнее альтернатива аi; между альтернативами аi и аj нет предпочтительности; предпочтительнее альтернатива аj. Аксиома основана на допущении: на множестве альтернатив существует совершенное, рефлексивное и транзитивное отношение слабого предпочтения
Заметим, что если одновременно истинны два высказывания: то между a1 и a2 имеет место отношение безразличия: a1∼a2. Если же a1 Аксиома 3. Транзитивность. Соотношения предпочтения и эквивалентности исходов транзитивны. Если исход аi предпочтительнее исхода аj, а исход аj предпочтительнее исхода аk, то исход аi тоже предпочтительнее исхода аk. Аналогично, если исход аi эквивалентен исходу аj, а исход аj эквивалентен исходу аk, то исходы аi и аk тоже эквивалентны. Аксиома 4. Коммутативность. Предпочтение исхода аi исходу аj не зависит от порядка, в котором они названы и представлены. Аксиома 5. Независимость. Если исход аi предпочтительнее исхода аj и, кроме того, существует исход аk, который не оценивается относительно исходов аi и аj, то смесь исходов аi и аk предпочтительнее смеси исходов аj и аk. (Под смесью исходов аm и аn понимается исход, заключающийся в появлении одного из них с некоторой вероятностью, например исхода аm с вероятностью p, а исхода аn с дополнительной вероятностью 1-р.) Иначе говоря, предполагается, что отношение безразличия (предпочтения) между двумя альтернативами не нарушается наличием третьего: (∀a1, a2 ) {(a1∼a2) ⇒ (∀a3)(∀p∈ (0, 1)) [(p, a1; (1-p), a3) ∼ (p, a2; (1-p), a3)]}. Согласно теории полезности при выполнении в реальной задаче оценки систем всех пяти аксиом существует функция полезности, однозначно определенная на множестве всех альтернатив с точностью до монотонного строго возрастающего линейного преобразования, иначе полезность измеряется в шкале интервалов. Важно подчеркнуть, что функция полезности характеризует лишь относительную, а не абсолютную предпочтительность альтернатив. Так, если F(a1) = 2, a F(a2) = 1, отнюдь не следует, что альтернатива а1 всегда в два раза или на единицу предпочтительнее альтернативы а2. Стоит произвести линейное преобразование функции полезности, и эти значения оценок будут уже другими. В зависимости от типа показателей исходов операции функция полезности может быть либо непрерывной, либо дискретной. Функцию полезности называют прямой, если, чем больше значение показателя исхода операции, тем он полезнее, и обратной, если, чем больше значение показателя исхода операции, тем менее он полезен. Функция полезности является универсальным и весьма удобным средством математического выражения предпочтений на множестве исходов операции. Процедура определения функции полезности включает три основных этапа: выявление показателей исходов операции, определение множества допустимых исходов операции и определение показателей полезности исходов операции. Определение полезности как меры оценки того или иного исхода операции представляет сложную задачу, точные методы решения которой пока не найдены. Все известные способы определения функции полезности носят приближенный характер и строятся на основе анализа влияния исходов исследуемой операции на операцию более высокого уровня иерархии, экспертных оценок и аппроксимации. Анализ влияния исходов исследуемой операции на операцию более высокого уровня иерархии основывается на моделировании и предполагает включение системы, с помощью которой реализуется исследуемая операция, как элемента в систему на один уровень выше и рассмотрение влияния на ее функционирование исходов исследуемой операции. Показатель исхода исследуемой операции будет выступать одним из управляемых параметров, описывающих вышестоящую операцию. В результате должна быть получена некоторая зависимость эффективности функционирования вышестоящей системы от интересующего нас показателя, которая и принимается в качестве функции полезности для исходов исследуемой операции. Так, чтобы найти значения полезности на исходах операции по передаче команд в сети оповещения, необходимо рассмотреть всю операцию перевода системы управления в повышенные степени боевой готовности. Если удастся определить, как влияет время оповещения на вероятность приведения системы в требуемую степень боевой готовности, то полученная функция будет функцией полезности. Достоинство способа относительно высокая объективность. Субъективные моменты в оценку полезности хотя и вносятся, но не прямо, как при других способах, а косвенным образом (через построение модели операции, которую выполняет вышестоящая система). Основной же недостаток состоит в трудностях реализации. Переход к системам и операциям более высокого уровня, естественно, сопровождается повышением сложности их анализа. Поэтому для оценки решений в условиях дефицита времени этот способ вряд ли может быть рекомендован. К нему прибегают преимущественно при предварительном исследовании операций, особенно тех, которые имеют вспомогательное назначение. Способы определения функции полезности с использованием методов экспертных оценок предполагают, что практический опыт и знания людей трудно заменить дедуктивными построениями формального характера. В силу этого способам на экспертной основе присущи известные преимущества по сравнению с другими и они интенсивно развиваются. При любом способе выполнения экспертизы в ней можно выделить следующие основные этапы: · упорядочение множества исходов операции по их предпочтительности · определение полезности каждого исхода F(ai), проверка полученных оценок на непротиворечивость путем сравнения оценок предпочтительности показателей полезности исходов; · устранение противоречий в оценках путем корректировки или варианта упорядочения исходов либо показателей полезности, либо того и другого вместе.
полезности: 1 - одноступенчатое; 2 - косинусоидальное; 3 - треугольное функция полезности. Наиболее простыми аппроксимациями являются одноступенчатое, косинусоидальное и треугольное представление функций полезности (рис. 2.) Одноступенчатое представление функции полезности (линия 1) может быть приемлемым для операций, в которых показателем исхода является срок выполнения работ, например подготовка презентации в ситуационном центре. В этом случае под исходами А понимается фактическое время готовности компьютерной системы презентации к работе, время начала презентации а0 - характерная точка. Очевидно, что полезность системы при ai Косинусоидальное и треугольное представления функции полезности (линии 2 и 3) могут быть приемлемы для операций, в которых показателем исхода является интервал времени, например подготовка системы телеконференции в локальной сети. Установленное время готовности а0. Включение системы в работу ранее установленного срока может привести к ограничению пропускной способности сети для других приложений. При задержке готовности растет вероятность того, что отдельные пользователи откажутся от участия в телеконференции. Минимально и максимально допустимые значения времени готовности равны соответственно amin и аmах. Совместно с а0 (amin<а0<аmах) эти величины представляют характерные точки. В зависимости от предпочтений ЛПР функция полезности может быть представлена либо отрезком косинусоиды, либо треугольником, построенным по этим точкам.
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 434. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 Таким образом, полезность исхода операции это действительное число, приписываемое исходу операции и характеризующее его предпочтительность по сравнению с другими альтернативами относительно цели.
Таким образом, полезность исхода операции это действительное число, приписываемое исходу операции и характеризующее его предпочтительность по сравнению с другими альтернативами относительно цели.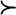 аj), как это, например, показано на рис. 2.8.
аj), как это, например, показано на рис. 2.8.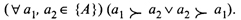
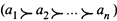 ;
;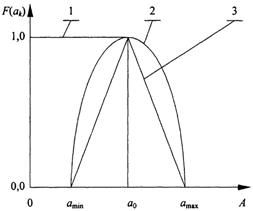 Определение функции полезности на основе аппроксимации заключается в следующем. При рассмотрении исходов конкретной операции отыскиваются характерные точки, соответствующие, например, экстремумам функции полезности, а неизвестные значения между ними определяются некоторой известной зависимостью. Вид аппроксимации выбирается на основе имеющихся сведений или качественных соображений о показателях полезности исходов. На практике могут применяться многоступенчатая Рис. 2.9. Представление аппроксимации
Определение функции полезности на основе аппроксимации заключается в следующем. При рассмотрении исходов конкретной операции отыскиваются характерные точки, соответствующие, например, экстремумам функции полезности, а неизвестные значения между ними определяются некоторой известной зависимостью. Вид аппроксимации выбирается на основе имеющихся сведений или качественных соображений о показателях полезности исходов. На практике могут применяться многоступенчатая Рис. 2.9. Представление аппроксимации а0 равна 1, при aiа0 она равна 0.
а0 равна 1, при aiа0 она равна 0.