Общая запись оптимизационной ЭММ (задача оптимального программирования). Основные элементы и понятия.

Реализовать на практике принцип оптимальности это значит разработать и получить решение по модели: max(min) максимизировать или минимизировать функцию f(x) при ограничениях, где f(x1,x2,…,xn) – математическая запись критерия оптимальности -ЦФ. Max(min) f(x)=f(x1,x2,…,xn),x є D.

Обычно, приведенную модель записывают в виде:

Max(min) f(x1,x2,…,xn)

g1(x1,x2,…xn) {≤ , = , ≥ } b1      (1)

g2(x1,x2,…xn) {≤ , = , ≥ } b2     (2)

gn(x1,x2,…xn) {≤ , = , ≥ } bn

xi  ≥ 0, i=1,¯ n                           (3)

22.  Прогнозирование на основе кривой роста.  

Точечный прогоноз – называется единственное значение прогнозируемого показателя. Интервальный прогноз – осуществляется путем рассчета доверительного интервала.

23. ЭММ нелинейной оптимизации, пример. Трудности, порождаемые нелинейностью [3 стр.39-41].  

24. Выявление и устранение аномальных наблюдений во временных рядах [1 стр.148-149].

Особые случаи решения ЗЛП симплексным методом.

1ый особый случай решения ЗЛП: решение не единственное (линия уровня параллельна одной из линий на границе области допустимых решений). Это означает, что задача имеет бесконечное множество оптимальных решений. Его задают координаты точек отрезка с угловыми точками.

2ой особый случай решения ЗЛП – задача не имеет решения, т.к. область решений не ограничена сверху.

3ий особый случай решения ЗЛП – задача не имеет решения, т.к множество планов пусто, нет ни одной общей точки.

26. Статистические показатели динамики экономических процессов [1 стр.157-163].  

27. Матрица планирования транспортной задачи, учет особых случаев[1 стр.100-02].

Структура временных рядов экономических показателей.  

Временной ряд экономических показателей можно разложить на 4 структуро-образующих элемента:

1. Тренд (U_t) – устойчивое систематическое изменение процесса в течение продолжительного времени.

2. Сезонная компонента (V_t) – колебания, носящие строго периодический или близкий к нему характер и завершающиеся в течении года.

3. Циклическая компонента (C_t) – период колебаний составляет несколько лет.

4. Случайная компонента (ε_t) – составная часть временного ряда, остающаяся после выделения из него регулярных компонент.

Задача о назначениях, постановка и ЭММ.

С ее помощью можно получить ответ на вопрос типа Как распределить рабочих по станкам, чтобы общая выработка была наибольшей? Как наилучшим образом распределить экипажи самолетов? Как назначить людей на разные должности? Исходные данные группируются в таблице, которая называется матрицей оценок, а результаты – в матрице назначений. ЕЕ постановка: Имеется n –работников, которые могут выполнить n-работ, причем использование i-того работника на j-той работе приносит доход Cij. Требуется поручить каждому из работников выполнение одной вполне определенной работы, чтобы максимизировать суммарный доход. Задача в том, чтобы найти распределение X=(Xij) работников по работам, которое максимизирует ЦФ.

F(x)=∑∑Cij Xij → max

∑Xij=1, i=1,n (1)

∑Xij=1, j=1,n (2)

причем Xij= либо 0 либо 1 для всех i,j=1,n

Ограничение (1) отражает условие того, что за каждым работником может быть закреплена только одна работа, а ограничение (2) означает, что для выполнения каждой работы может быть выделен только один работник. При решении таких задач используются алгоритмы и методы решения транспортных задач, в частности метод потенциалов.

Процедура прогнозирования с использованием кривых роста, этапы и наиболее часто используемые кривые роста.

Этапы: 1. Предварительный анализ данных. 2. Построение моделей: формирование набора аппроксимирующих функций (кривых роста) и численное оценивание параметров моделей. 3. Проверка адекватности моделей и оценка их точности. 4. Выбор лучшей модели. 5. Расчет точечного и интервального прогонозов.

Наиболее часто используемы кривые роста: полиномиальные , экспоненциальные 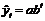, где a и b – положительные числа, S-образные

31. Матричная и векторная формы записи ЗЛП [3 стр.17-18].