
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основные свойства задачи линейного программирования.В основе математического метода получения оптимального решения лежат основные свойства ЗЛП: 1.Не существует локального экстремума отличного от глобального. Если экстремум есть, то он единственный. 2.Множествовсех планов ЗЛП является выпуклой многогранной областью (многогранником решения). 3.ЦФв ЗЛП достигает своего max (min) значения в угловой точке многогранника решения (в вершине). Если ЦФ принимает max решение более чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек. 4.Каждойугловой точке отвечает опорный план ЗЛП (не отрицательное базисное решение соответствующей КЗЛП)
Методы выявления тенденций во временных рядах. Для определения наличия тренда во временном ряду применяется несколько методов. 1.Метод проверки разностей средних уровней. Состоит из 4х этапов: I: Вр. Ряд разбивается на две примерно равные по числу уровней части (n1+n2=n). II: Для каждой из этих частей вычисляются средние значения и дисперсии.
III: Проверка равенства (однородности) дисперсий обеих частей ряда с помощью F-критерия Фишера.
Если расчетное значение F меньше табличного Fα, то гипотеза о равенстве дисперсий принимается и переходят к 4му этапу. IV: Проверяется гипотеза об отсутствии тренда с использованием t-критерия Стьюдента. Для этого определяется рассчетное значение критерия Стьюдента по формуле:
, где
Если расчетное значение t меньше табличного значение статистики Стьюдента tα, тренда нет. Если больше – тренд есть. 2.Метод Фостера-Стьюарта.
|
||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 328. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
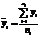

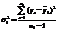
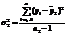


 - среднеквадратичексое отклонение разности средних:
- среднеквадратичексое отклонение разности средних: