
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Двойственные оценки в ЗЛП, интервалы устойчивости двойственных оценок, определение средствами Excel.С каждой задачей линейного программирования тесно связана другая линейная задача , называемая двойственной; первоначальная задача называется исходной или прямой. Связь исходной и двойственной задачи заключается, в частности, в том, что решение одной из них может быть получено непосредственно из решения другой. Переменные двойственной задачи Модель двойственной задачи имеет вид:
Теорема об оценках: значения переменных
Экономико- математический анализ оптимальных решений базируется на свойсвах двойственных оценок (для определения этих границ существует математические соотношения, которые реализованы в «Отчете по устойчивости» Excel. (теневые цены, интервалы устойчивости, допустимое увеличение, допустимое уменьшение) Интервалы изменения объемов ресурсов ( компонент вектора В) в пределах которых двойственные оценки сохраняют свои значения принято называть интервалами устойчивости двойственных оценок. Если двойственные оценки попадают в интервал устойчивости, то экономическое поведение не меняется Если выходят за пределы интервалов устойчивости ,то новое экономическое поведение получим в новом решении задачи. 1. те ограничения которые выполнялись как равенства , так и будут выполняться как равенства 2.структура плана останется неизменной Совмещая 1 и 2 формируем новое поведение объемов ресурсов. Двойственные оценки связаны с  оптимальным планом простой задачи .Всякое изменение исходных данных прямой задачи может оказать влияние как на ее оптимальный план (
Методы механического сглаживания временных рядов. Суть методов механического сглаживания заключается в следующем: берется несколько первых уровней временного ряда, образующих интервал сглаживания. Для них подбирается полином, степень которго должна быть меньше числа уровней, входящих в интервал сглаживания; с помощью полинома определяются новые, выравненные значения уровней в середине интервала сглаживания. Далее интервал сглаживания сдвигается на один уровень ряда вправо, вычисляется следующее сглаженно значение, и т.д. Самым простым является метод простой скользящей средней. Метод взвешенной скользящей средней Метод экспоненциального сглаживания.
Принцип оптимальности в планировании и управлении, его математическая запись. Суть принципа оптимальности состоит в стремлении выбрать такое управленческое решение, которое наилучшим образом учитывало бы внутренние возможности и внешние условия производственной деятельности хозяйствующего субъекта. Слова «наилучшим образом» в принципе оптимальности на практике означают – выбор некоторого экономического показателя, позволяющего сравнивать, оценивать эффективность управленческих решений Х, т.е. выбрать критерий оптимальности. Критерии оптимальности: минимум себестоимости продукции, максимум прибыли от реализации, максимум рентабельности и др. Слова «учитывало бы внутренние возможности и внешние условия» на практике означают, что на выбор управленческого решения Х накладывается ряд ограничений, т.е. выбор Х осуществляется из некоторой области допустимых решений D. Реализовать на практике принцип оптимальности это значит разработать и получить решение по модели: максимизировать или минимизировать функцию f(x) при ограничениях, где f(x1,x2,…,xn) – математическая запись критерия оптимальности –ЦФ оптимизационной модели. Max(min) f(x1,x2,…,xn) g1(x1,x2,…xn) {≤ , = , ≥ } b1 g2(x1,x2,…xn) {≤ , = , ≥ } b2 gn(x1,x2,…xn) {≤ , = , ≥ } bn xi ≥ 0, i=1,¯ n
|
|||||
|
Последнее изменение этой страницы: 2018-05-30; просмотров: 491. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 называются двойственными оценками.
называются двойственными оценками. g(
g(  )=
)= 


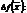
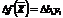
 ) так и на систему оптимальных двойственных оценок. Поэтому чтобы проводить экономический анализ с использованием двойственных оценок,нужно знать их интервал устойчивости
) так и на систему оптимальных двойственных оценок. Поэтому чтобы проводить экономический анализ с использованием двойственных оценок,нужно знать их интервал устойчивости