
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Решение систем линейных уравнений. Метод обратной матрицы
Перейдем к изучению СЛАУ (4.1), которой соответствует матричное уравнение (4.2). Сначала рассмотрим частный случай, когда число неизвестных равно числу уравнений данной системы ( Следовательно, с учетом свойств умножения матриц получаем Так как
Убедимся, что найденное значение Покажем, что это решение единственное. Пусть матричное уравнение (4.2) имеет другое решение
Покажем, что матрица С этой целью умножим предыдущее равенство слева на матрицу В результате получим
Такое решение системы Пример. Найти решение системы Выпишем матрицу системы:
Для этой матрицы ранее (занятие 1) мы уже нашли обратную:
Здесь мы вынесли общий множитель
Ищем решение по формуле:
Найденные значения переменных подставляем в уравнения системы и убеждаемся, что они являются ее решением.
Комплексные числа. Алгебраическая, тригонометрическая и показательная форма комплексных чисел Комплексное число — это выражение вида a + bi, где a, b — действительные числа, а i — так называемая мнимая единица, символ, квадрат которого равен –1, то есть i2 = –1. Число aназывается действительной частью, а число b — мнимой частьюкомплексного числа z = a + bi. Если b = 0, то вместо a + 0i пишут просто a. Видно, что действительные числа — это частный случай комплексных чисел.  Арифметические действия над комплексными числами те же, что и над действительными: их можно складывать, вычитать, умножать и делить друг на друга. Сложение и вычитание происходят по правилу (a + bi) ± (c + di) = (a ± c) + (b ± d)i, а умножение — по правилу (a + bi) · (c + di) = (ac – bd) + (ad + bc)i (здесь как раз используется, что i2 = –1). Число
(Например, Алгебраическая форма комплексного числа
Запись комплексного числа z в виде
Например
Тригонометрическая форма комплексного числа
Если
Показательная форма комплексного числа
Показательной формой комплексного числа
|
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 247. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ) и
) и  , то есть основная матрица системы
, то есть основная матрица системы  невырождена. В этом случае, согласно предыдущему пункту, для матрицы
невырождена. В этом случае, согласно предыдущему пункту, для матрицы  . Ясно, что она согласована с матрицами
. Ясно, что она согласована с матрицами  и
и  . Покажем это. Для этого умножим слева обе части матричного уравнения (4.2) на матрицу
. Покажем это. Для этого умножим слева обе части матричного уравнения (4.2) на матрицу 

 , а
, а  , тогда
, тогда . (4.3)
. (4.3) является решением исходной системы. Подставив (4.3) в уравнение (4.2), получим
является решением исходной системы. Подставив (4.3) в уравнение (4.2), получим  , откуда имеем
, откуда имеем  .
. , которое удовлетворяет равенству
, которое удовлетворяет равенству .
.
 уравнений с
уравнений с 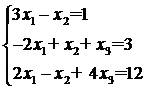 .
. ,
, 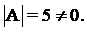

 или
или , так как нам в дальнейшем нужно будет произведение
, так как нам в дальнейшем нужно будет произведение  .
.

 = a – bi называется комплексно-сопряженнымк z = a + bi. Равенство z ·
= a – bi называется комплексно-сопряженнымк z = a + bi. Равенство z ·  .
. .)
.) , где a и b - действительные числа, называется алгебраической формой комплексного числа.
, где a и b - действительные числа, называется алгебраической формой комплексного числа. .
. - модуль комплексного числа
- модуль комплексного числа  - его аргумент, то тригонометрической формой комплексного числа z называется выражение
- его аргумент, то тригонометрической формой комплексного числа z называется выражение 
