
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Методы нахождения ранга матрицыСуществует 2 метода нахождения ранга матрицы. Рассмотрим их. Метод элементарных преобразований нахождения ранга матрицы Метод элементарных преобразований нахождения ранга матрицы заключается в том, что матрицу A приводят к ступенчатому виду с помощью элементарных преобразований; количество ненулевых строк полученной ступенчатой матрицы есть искомый ранг матрицы A. Метод окаймляющих миноров нахождения ранга матрицы Метод окаймляющих миноров нахождения ранга матрицы A состоит в следующем. Необходимо: Найти какой-нибудь минор M1 первого порядка (то есть элемент матрицы), отличный от нуля. Если такого минора нет, то матрица A нулевая и r(A)=0. Вычислять миноры 2-го порядка, содержацие M1 (окаймляющие M1) до тех пор, пока не найдется минор M2, отличный от нуля. Если такого минора нет, то r(A)=1, если есть, то r(A)?2. И т.д. Вычислять (если они существуют) миноры k-о порядка, окамляющие минор Mk-1?0. Если таких миноров нет, или они все равны нулю, то r(A)=k-1; если хотя бы один такой минор Mk?0, то r(A)?k, и процесс продолжается. При нахождении ранга матрицы таким способом достаточно на каждом шаге найти всего один ненулевой минор k-го порядка, причем искать его только среди миноров, содержащих минор Mk-1?0.
Системы линейных уравнений Система линейных алгебраических уравнений (линейная система, также употребляются аббревиатуры СЛАУ, СЛУ) — система уравнений, каждое уравнение в которой является линейным — алгебраическим уравнением первой степени. В классическом варианте коэффициенты при переменных, свободные члены и неизвестные считаются вещественными числами, но все методы и результаты сохраняются (либо естественным образом обобщаются) на случай любых полей, например, комплексных чисел.  Решение систем линейных алгебраических уравнений — одна из классических задач линейной алгебры, во многом определившая её объекты и методы. Кроме того, линейные алгебраические уравнения и методы их решения играют важную роль во многих прикладных направлениях, в том числе в линейном программировании, эконометрике.
Системой линейных алгебраических уравнений (СЛАУ) называется система вида:
Решением системы (4.1) называется такая совокупность n чисел Решить систему означает найти все ее решения или доказать, что ни одного решения нет. СЛАУ называется совместной, если она имеет хотя бы одно решение, и несовместной, если она решений не имеет. Если совместная система имеет только одно решение, то она называется определенной, и неопределенной, если она имеет более чем одно решение. Например, система уравнений несовместная, а система Две системы уравнений называются равносильными или эквивалентными, если они имеют одно и то же множество решений. В частности, две несовместные системы считаются эквивалентными. Основной матрицей СЛАУ (4.1) называется матрица А размера Матрицей неизвестных СЛАУ (4.1) называется матрица-столбец Х, элементами которой являются неизвестные системы (4.1): Матрицей свободных членов СЛАУ (4.1) называется матрица-столбец В, элементами которой являются свободные члены данной СЛАУ: С учетом введенных понятий СЛАУ (4.1) можно записать в матричном виде
|
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 214. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (4.1)
(4.1) , при подстановке которых каждое уравнение системы обращается в верное равенство.
, при подстановке которых каждое уравнение системы обращается в верное равенство. совместная и определенная, так как имеет единственное решение
совместная и определенная, так как имеет единственное решение 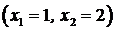 ; система
; система 
 совместная и неопределенная, так как имеет более одного решения
совместная и неопределенная, так как имеет более одного решения  .
. , элементами которой являются коэффициенты при неизвестных данной системы, то есть
, элементами которой являются коэффициенты при неизвестных данной системы, то есть .
. .
.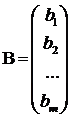 .
. или
или . (4.2)
. (4.2)