
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Моделювання пуассоновського потоку.
Візьмем найпростіший (пуассоновський) потік вимог з інтенсивністю
Мал 1. 1
Функція розподілу
Знайдемо ймовірність того, що випадкова величина
Тут
Щоб знайти функцію щільності розподілу випадкової величини
Це є функція щільності експонціального закону розподілу. Графіки функцій
Мал. 1.2
Таким чином, щоб одержати пуассоновський потік вимог, які надходять у систему, досить згенерувати випадкову величину з експоненціальним законом розподілу.
1.6. Організація черги.
Дисципліни постановки вимог у чергу й вибору вимог із черги для обслуговування визначають порядок за яким вимоги стають у чергу, якщо пристрій обслуговування зайнятий, і порядок їх виходу із черги для обслуговування, якщо пристрій для обслуговування вільний. Найпростіша дисципліна обслуговування передбачає постановку вимог у чергу один по одному по мірі їх надходження. Вона має назву перший прийшов – першим обслужений (ПППО), в англомовной літературі – FIFO (First In First Out). Прикладом черги з такою дисципліною може бути черга до телефона - автомата.  Є інший спосіб організації черги, коли для обслуговування вибираються останні в черзі вимоги (останній прийшов – першим обслужений) (ПППО), в англомовной літературі LIFO (Last In First Out). Цей спосіб ще називається «стеком» або «магазином». Прикладом черги з такою дисципліною обслуговування може служити паром для перевезення авто, - автомобіль, який заїхав на паром першим, залишає паром останнім. Вибір вимог із черги також може бути випадковим. (в англомовной літературі – RANDOM). Наприклад, вибір куль із барабана при грі в лото. При виборі вимог із черги може також ураховуватися пріоритет. Черга може мати обмеження по довжині або за часом перебування вимог у ній. У цьому випадку вимоги, що знову надійшли, залишають систему без обслуговування.
Вихідний потік вимог.
Вихідний потік – це потік вимог, які залишають систему. При цьому вимоги можуть бути як обслуженими, так і не обслуженими. Імовірнісні характеристики розподілу вимог вихідного потоку в часі залежать від щільності розподілу вхідного потоку й параметрів роботи пристроїв обслуговування. З теорії масового обслуговування відомо, що вихідний потік вимог СМО з М пристроями обслуговування із чергами для найпростішого вхідного потоку з параметром
1.8 Режими роботи СМО.
На практиці часто доводиться вивчати режими СМО, за допомогою яких описується деякі виробничі процеси або система обробки інформації. Якщо в системі пристрої для обслуговування час від часу виходять із ладу, то вводиться поняття режим відмови. При дослідженні деяких систем потрібно брати до уваги ще один режим – блокування обслуговування. Цей режим обумовлений тимчасовими перериваннями або затримкою процесів обслуговування. Зміна режиму роботи СМО може бути викликана зовнішнім впливом (тимчасовою відсутністю вимог, ремонтом устаткування й т.п.) або виходом з ладу деякого пристрою системи (наприклад, блоку живлення в комп'ютері).
Типи моделей СМО.
У теорії масового обслуговування розглядаються тільки такі СМО, параметри ефективності яких можна одержати аналітично. Для позначення таких систем і їх моделей часто використовують запис, запропонований Канделом – Тут Найпоширенішою моделлю, яка розглядається в теорії масового обслуговування, є модель типу Модель типу У теорії масового обслуговування аналітичні результати отримані тільки для моделей типу
Аналіз СМО. Мережі СМО. Формула Літтла. В теорії масового обслуговування важливе значення має формула Літтла (закон збереження стаціонарної черги), яка дозволяє визначити середню кількість вимог, що перебувають у системі. Щоб одержати формулу Літтла, розглянемо СМО загального виду, зображену на малюнку 2.1 у вигляді «чорного ящика», і будемо розглядати її вхідні й вихідні потоки вимог.
Мал. 2.1 Позначимо через
Мал. 2.2 Кількість вимог
Інтенсивність надходження вимог у СМО за час спостереження
Заштрихована площа між кривими Середній час перебування вимог у системі можна знайти так:
Середня кількість вимог, що перебувають у системі за проміжок часу
Використовуючи формули (7-9), можна отримати:
Візьмемо граничні значення величин, що входять в (10) при
У такий спосіб:
Таким чином, для будь-якого закону розподілу проміжків часу між двома моментами надходження вимог і будь-якого розподілу часу їхнього обслуговування, будь-якої кількості пристроїв обслуговування, будь-якої дисципліни обслуговування середня кількість вимог, що перебувають у системі
Одноканальні СМО. Розглянемо одноканальну СМО з одним пристроєм обслуговування
Мал. 2.3 Позначимо через
Якщо позначити середній час обслуговування вимоги в пристрої через
Для СМО з одним пристроєм обслуговування завжди має місце рівність:
де
Знайдемо коефіцієнт завантаження (використання) пристрою обслуговування
де Інакше:
Можна показати, що
де Введемо коефіцієнт варіації
Для експонентного закону розподілу коефіцієнт варіації Можна показати, що для моделі СМО типу
Середній час перебування вимоги в такій системі знаходиться за формулою:
З (20) можна знайти середній час очікування вимоги в черзі:
Зазвичай цікавляться нормованим часом очікування:
Для моделей типу
Для моделей типу
Вочевидь СМО з регулярним законом обслуговування характеризується середнім часом очікування, який в 2 раза менший за середній час очікування в СМО з експоненціальним законом обслуговування. Це закономірно, оскільки час перебування вимог у системі і їхня кількість пропорційні дисперсії часу обслуговування.
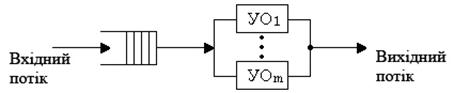
Багатоканальні СМО Багатоканальні СМО – це СМО з декількома однаковими пристроями обслуговування, що ввімкнені паралельно (мал. 2.4).
Мал. 2.4
Аналіз багатоканальних СМО набагато складніший, ніж одноканальних. За допомогою теорії масового обслуговування можна отримувати аналітичні залежності в замкнутому вигляді для розрахунку характеристик роботи багатоканальних СМО в стаціонарному режимі роботи тільки лише для моделей типу Для системи, що складається з
Його можна трактувати як математичне очікування числа зайнятих пристроїв.
|
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 361. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (мал.1.1). Позначимо через
(мал.1.1). Позначимо через
 проміжки часу між двома сусідніми вимогами. Очевидно, що
проміжки часу між двома сусідніми вимогами. Очевидно, що  дає ймовірність того, що випадкова величина
дає ймовірність того, що випадкова величина  , тобто
, тобто (2)
(2)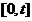 з'явилася хоча б одна вимога. З урахуванням формули (1) можна записати:
з'явилася хоча б одна вимога. З урахуванням формули (1) можна записати: (3)
(3) є ймовірність того, що в інтервалі часу
є ймовірність того, що в інтервалі часу  . Таким чином,
. Таким чином,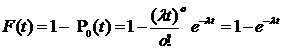 (4)
(4) (5)
(5)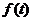 й
й  показані на малюнку 1.2.
показані на малюнку 1.2.
 і експоненціальним розподілом часу обслуговування з параметром
і експоненціальним розподілом часу обслуговування з параметром  є найпростішим потоком з параметром
є найпростішим потоком з параметром  . В інших випадках розподіл імовірності вихідних потоків вимог СМО має складну імовірнісну природу.
. В інших випадках розподіл імовірності вихідних потоків вимог СМО має складну імовірнісну природу. .
. – розподіл часу надходження вимог.
– розподіл часу надходження вимог.  – розподіл часу обслуговування.
– розподіл часу обслуговування.  – кількість пристроїв для обслуговування.
– кількість пристроїв для обслуговування. . У цій моделі тільки один пристрій обслуговування (цифра 1) і в ній процеси розподілу часу надходження (перша буква М) і обслуговування (друга буква М) є Марковськими. У такій моделі час між двома вимогами, які надійшли у систему, й час їх обслуговування мають експоненціальні розподіли.
. У цій моделі тільки один пристрій обслуговування (цифра 1) і в ній процеси розподілу часу надходження (перша буква М) і обслуговування (друга буква М) є Марковськими. У такій моделі час між двома вимогами, які надійшли у систему, й час їх обслуговування мають експоненціальні розподіли. - детермінована, а модель типу
- детермінована, а модель типу 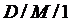 - змішана. Якщо відомостей про систему мало, її модель позначається як
- змішана. Якщо відомостей про систему мало, її модель позначається як  .
. ,
, 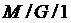 . Для визначення характеристик моделей з іншими значеннями параметрів СМО потрібно використовувати методи імітаційного моделювання.
. Для визначення характеристик моделей з іншими значеннями параметрів СМО потрібно використовувати методи імітаційного моделювання.
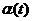 випадковий процес надходження вимог (заявок) у систему за інтервал часу
випадковий процес надходження вимог (заявок) у систему за інтервал часу 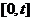 . Через
. Через  позначимо процес виходу вимог із системи на тому ж проміжку часу. Представимо обидва процеси графічно (мал.2.2):
позначимо процес виходу вимог із системи на тому ж проміжку часу. Представимо обидва процеси графічно (мал.2.2):
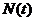 , що перебувають у системі в будь-який момент часу
, що перебувають у системі в будь-який момент часу  (6)
(6) (7)
(7)
 (8)
(8) (9)
(9) (10)
(10) .
. ;
;  ;
;  .
. (11)
(11)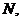 визначається через інтенсивність надходження вимог
визначається через інтенсивність надходження вимог 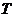 .
. й чергою до нього
й чергою до нього  (мал. 2.3).
(мал. 2.3).
 середній час перебування вимоги в черзі. Тоді відповідно до формули Літтла можна отримати середню кількість вимог у черзі:
середній час перебування вимоги в черзі. Тоді відповідно до формули Літтла можна отримати середню кількість вимог у черзі: (12)
(12) і розглядати СМО як систему з одним пристроєм, то, використовуючи формулу Літтла, можна визначити середню кількість вимог у пристрої для обслуговування:
і розглядати СМО як систему з одним пристроєм, то, використовуючи формулу Літтла, можна визначити середню кількість вимог у пристрої для обслуговування: (13)
(13) (14)
(14) середній час перебування вимоги в системі.
середній час перебування вимоги в системі. . Його можна визначити як частку від ділення інтенсивності надходження вимог у систему
. Його можна визначити як частку від ділення інтенсивності надходження вимог у систему  , тобто:
, тобто: , (15)
, (15)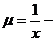 швидкість обслуговування вимог пристроєм обслуговування.
швидкість обслуговування вимог пристроєм обслуговування.
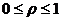 (16)
(16) (17)
(17) ймовірність того, що в момент надходження вимоги в систему, пристрій обслуговування буде вільним.
ймовірність того, що в момент надходження вимоги в систему, пристрій обслуговування буде вільним.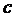 як відношення стандартного відхилення
як відношення стандартного відхилення  від середнього значення до самого середнього значення
від середнього значення до самого середнього значення  :
: (18)
(18) оскільки
оскільки 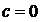 (
(  ).
). середня кількість вимог у системі визначається формулою:
середня кількість вимог у системі визначається формулою: (19)
(19)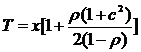 (20)
(20) (21)
(21) (22)
(22) :
:


 Для СМО з іншими законами розподілу часу надходження й обслуговування вимог, використовують чисельні методи.
Для СМО з іншими законами розподілу часу надходження й обслуговування вимог, використовують чисельні методи. однакових пристроїв обслуговування коефіцієнт завантаження дорівнює:
однакових пристроїв обслуговування коефіцієнт завантаження дорівнює: