
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Расчёт изгибаемых элементов из цельной и клееной древесины на плоский поперечный и косой изгибВ соответствии с ТКП 45-5.05-146-2009 по п. 7.4 расчет изгибаемых элементов на прочность по нормальным напряжениям следует производить по формуле
где Для элементов из цельной древесины При определении Для составных элементов на податливых связях Расчет изгибаемых элементов на прочность при скалывании следует производить по формуле
где Расчет элементов цельного сечения на прочность при косом изгибе следует производить по формуле
где Количество срезов связей
где  При наличии в шве связей разной несущей способности, но одинаковых по характеру работы (например, нагелей и гвоздей), их несущие способности следует суммировать. Для изгибаемых элементов, не имеющих постоянного подкрепления сжатой кромки из плоскости изгиба, следует производить проверку устойчивости плоской формы деформирования по формуле
где Коэффициент
где При подкреплении из плоскости изгиба в промежуточных точках растянутой кромки элемента на участке lmкоэффициент kinst следует умножать на коэффициент kr,m, При расчете изгибаемых элементов с линейно меняющейся по длине высотой и постоянной шириной поперечного сечения, не имеющих закреплений из плоскости его растянутой кромки, коэффициент
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 387. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 — расчетный изгибающий момент;
— расчетный изгибающий момент; 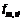 — расчетное сопротивление изгибу;
— расчетное сопротивление изгибу; 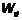 — расчетный момент сопротивления поперечного сечения элемента.
— расчетный момент сопротивления поперечного сечения элемента. .
. ослабления сечений, расположенные на участке длиной до 200 мм, следует принимать совмещенными в одном расчетном сечении.
ослабления сечений, расположенные на участке длиной до 200 мм, следует принимать совмещенными в одном расчетном сечении. значения коэффициента
значения коэффициента  для элементов из одинаковых слоев приведены в таблице 7.3.
для элементов из одинаковых слоев приведены в таблице 7.3.
 ,
,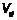 — расчетная поперечная сила;
— расчетная поперечная сила;  — статический момент брутто сдвигаемой части поперечного сечения элемента относительно нейтральной оси;
— статический момент брутто сдвигаемой части поперечного сечения элемента относительно нейтральной оси;  — момент инерции брутто поперечного сечения элемента относительно нейтральной оси;
— момент инерции брутто поперечного сечения элемента относительно нейтральной оси;  — расчетная ширина сечения элемента;
— расчетная ширина сечения элемента; 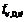 — расчетное сопротивление древесины скалыванию при изгибе.
— расчетное сопротивление древесины скалыванию при изгибе.
 и
и  — составляющие расчетного изгибающего момента для главных осей сечения Х и У;
— составляющие расчетного изгибающего момента для главных осей сечения Х и У;  и
и  — расчетные моменты сопротивления поперечного сечения относительно главных осей Х и У.
— расчетные моменты сопротивления поперечного сечения относительно главных осей Х и У. равномерно расставленных в каждом шве составного элемента на участке с однозначной эпюрой поперечных сил, должно удовлетворять условию
равномерно расставленных в каждом шве составного элемента на участке с однозначной эпюрой поперечных сил, должно удовлетворять условию ,
,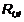 — расчетная несущая способность связи в данном шве;
— расчетная несущая способность связи в данном шве;  и
и  — изгибающие моменты в начальном А и конечном В сечениях рассматриваемого участка.
— изгибающие моменты в начальном А и конечном В сечениях рассматриваемого участка.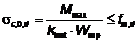 ,
, —максимальный изгибающий момент на рассматриваемом участке
—максимальный изгибающий момент на рассматриваемом участке  ;
;  — момент сопротивления брутто на том же участке;
— момент сопротивления брутто на том же участке; 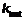 — коэффициент устойчивости изгибаемого элемента.
— коэффициент устойчивости изгибаемого элемента.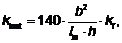
 — расстояние между точками закрепления сжатой кромки от смещения из плоскости изгиба;b — ширина поперечного сечения;h —максимальная высота поперечного сечения на участке lm;kf— коэффициент, зависящий от формы эпюры изгибающих моментов на участке lm, определяемый по таблице 7.4.
— расстояние между точками закрепления сжатой кромки от смещения из плоскости изгиба;b — ширина поперечного сечения;h —максимальная высота поперечного сечения на участке lm;kf— коэффициент, зависящий от формы эпюры изгибающих моментов на участке lm, определяемый по таблице 7.4. зависящий от формы эпюры моментов по длине lmи принимаемый по таблице
зависящий от формы эпюры моментов по длине lmи принимаемый по таблице