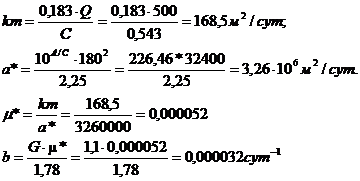Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
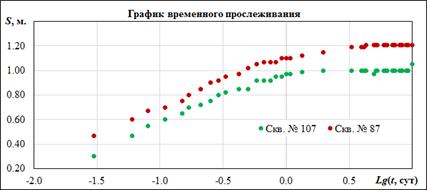
Опытно-фильтрационные работы.Опытно-фильтрационные работы проводились на скважинах с целью определения основных гидродинамических параметров водоносного горизонта и параметра перетекания. Работы проводились по схеме кустовой откачки с наблюдениями за динамикой уровня в наблюдательных скважинах № 107 (верхний валанжин) и 87 (нижний валанжин), расположенных на расстоянии 180 метров от возмущающей (центральной) скважины № 107Д (нижний валанжин). Результаты наблюдений за динамикой уровня в скважинах представлены в таблице 4.1. Характер понижений уровня свидетельствует о следующем. Таблица 4.1. Журнал ОФР по скважинам Северного участка
1. Уже через 2–3 суток отмечается стабилизация понижения в наблюдательных скважинах. То есть, режим очень быстро переходит в стационарный. 2. Форма выходных кривых временного прослеживания (рис.4.2.) свидетельствует о том, что с позиций гидродинамики верхневаланжинский и и нижневаланжинский водоносные отложения представляют собой единый водоносный горизонт. Принятое многими авторами деление валанжина на два обосновано только с позиций выраженной гидрогеохимической зональности. Учитывая это, в дальнейшем будем придерживаться сложившихся представлений.
Рис. 4.2. График временного прослеживания по кусту скважин № 87, № 107. Центральная – скв. № 107Д.
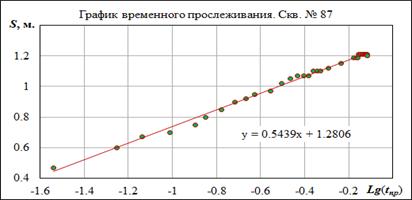
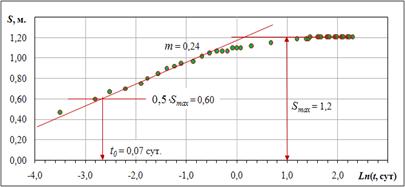
3. Небольшая разница в понижениях скважин № 107 и 87 может быть объяснена несовершенством их по степени вскрытия. 4. Для таких условий интерпретация данных ОФР возможна с использованием методики Хантуша или Хантуша-Джейкоба [21]. Расчет по методике Хантуша (по скв. № 87) представлен ниже. Уклон (m) кривой графика временного прослеживания в координатах S÷Ln(t) (рис. 4.3) равен: где α – безразмерный параметр Фурье. При наличии перетекания, форма выходной кривой имеет точку перегиба (S = 0.5×Smax), где выполняется условие:
где r – расстояние до точки наблюдения от возмущающей скважины; Рис. 4.3. Интерпретация ОФР по Методике М. Хантуша.
t – текущее время от начала возмущения центральной скважины; а* – пъезопроводность пласта; Для точки перегиба справедливо соотношение: Функция ex×K0(x) затабулирована и имеется в справочной литературе. Из (4.8) определяют функцию ex×K0(x) при х = 2,50. По справочным данным r/B = 0,125. Далее определяют все емкостные и фильтрационные параметры:
5. Для стационарного режима предельный радиус влияния откачки можно определить по известной зависимости: Расчеты по скважине № 107, выполненные по аналогичной методике, дают следующие параметры: km = 241,7 м2/сут; а* = 3,0×106 м2/сут; m* = 0,00008; b = 0,000059 сут-1; R = 2200 м. И методика Хантуша и Тейса-Джейкоба несколько субъективны, поскольку определение углового коэффициента (m) или выбор палетки определяются исполнителем работ. Авторами разработан собственный метод, основанный на графоаналитической методике, объективность которой значительно выше. В основе лежат те же теоретические представления о динамике формирования понижения в процессе откачки планово-радиальной геофильтрации, возникающей при возмущении пласта откачкой из скважины. При возмущении неограниченного в плане и изолированного в разрезе водоносного пласта, динамика понижения уровня в любой точке, удаленной на расстояние r от точки взмущения, описывается известным уравнением Тейса:
где S – понижение уровня в скважинах при откачке; km – водопроводимость пласта; Ei(-a) экспоненциальная показательная функция. Схема изолированного в разрезе пласта используется наиболее часто. Собственно анализ ОФР с нее и начинается. И если выясняется, что динамика формирования понижения не может быть описана данной схемой, прибегают к более общей постановке, учитывающей гидравлическую связь с соседними горизонтами. Если принять допущение о постоянстве напоров в смежных горизонтах-донорах, что равнозначно предположению m0 ®¥, m00 ®¥ , то дифференциальное уравнение, характеризующее процесс формирования понижения, можно представить в виде [19]:
где b* – параметр перетекания: Решение (4.6) выражается следующим образом:
где W (a, r/B)– функция колодца; Функции Ei(-a) и W(a, r/B) затабулированы и приводятся в многочисленной справочной литературе. Авторами показано [22], что при выполнении условий с погрешностью < 6% функция колодца может быть заменена:
Подставляя (4.12) в (4.10), понижение уровня может быть представлено:
С учетом принятых обозначений: После несложных преобразований, получается простая и удобная для расчетов формула: Для изолированного в разрезе пласта (4.14) переходит в известное решение Джейкоба: Для интерпретации ОФР применялся метод подбора с использованием формулы (4.14). Перепишем его в следующем виде: где Ln(tпр) = Ln(t) – Ln(1+1,78.b .t/m*). Поскольку в приведенное время (tпр) входит соотношение неизвестных параметров b/m*, то приходится прибегать к методике подбора, суть которой заключается в следующем. - задается ряд соотношений Gi = 1,78×b/m* (i = 1, 2, 3)и для каждого случая рассчитывается приведенное время (tпр), по которым строится серия графиков в координатах S –Lg(tпр). - далее все графики усредняются полиномом второй степени:
где a, β, γ– некоторые эмпирические коэффициенты, определяемые методом наименьших квадратов. - из полученной серии выбирается график, который представляет собой прямую линию. Это просто сделать путем построения вспомогательного графика в координатах Gi ÷ g, и найти точку на оси Gi, соответствую g = 0. -дальнейшая интерпретация ОФР ничем не отличается от общеизвестного графоаналитического метода Тейса-Джейкоба. Решение задачи представлено по скважине № 87 по данным, представленным в таблице 41. Интерпретация результатов ОФР производилась по формуле (4.14). Было выбрано несколько значений G, для которых рассчитано приведенное время. Расчеты проводились для G = 0,0; 1,0; 2,0; 3,0, они даны в таблице 4.2. Графики прослеживания (для каждого G) представлены на рис. 4.4.
Табл. 4.2. Расчет приведенного времени (куст скв № 107Д/87). Наблюдения по скв. № 87.
Рис. 4.4. Графики временного прослеживания по скв. № 87. Решение задачи можно изобразить в виде таблицы 4.3. Таблица 4.3. Зависимость G от g
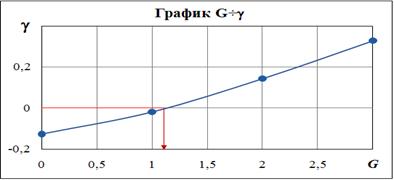
Вспомогательный график Gi ÷ g изображен на рис. 4.5. Искомое значение G = 1,1. Далее не составляет труда определить параметры, например, с помощью графоаналитического метода Тейса-Джейкоба. Графическое изображение решения дано на рис. 4.6. Линейная зависимость имеет вид S = А+С×Lg(tпр), где
Рис. 4.5. Вспомогательный график для определения G.
Искомые параметры равны:
Рис. 4.6. График временного прослеживания по скв. № 87.
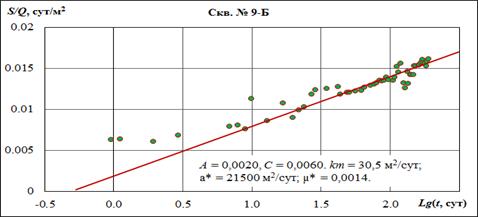
Несколько другая картина наблюдается по скважинам титонского горизонта. Этот горизонт более обособлен, гидравлическая связь его с валанжинским – более затруднена. На рис. 4.7 дан график временного прослеживания по кусту скважин № 7-РЭ (центральная) - № 9-Б (наблюдательная), оборудованные на титонский горизонт. Как видно, деформации графика не наблюдается даже через 100 сут, что свидетельствует о низком значении параметра перетекания.
Рис. 4.7. График временного прослеживания по кусту скв. № 7-РЭ/9-Б.
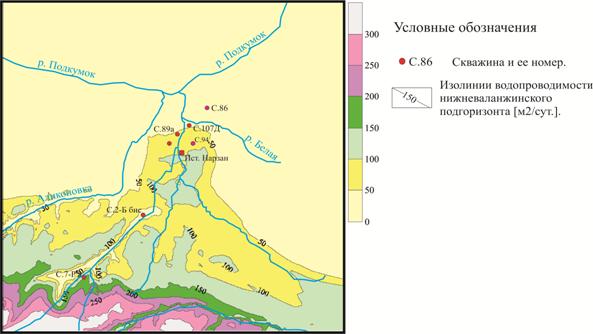
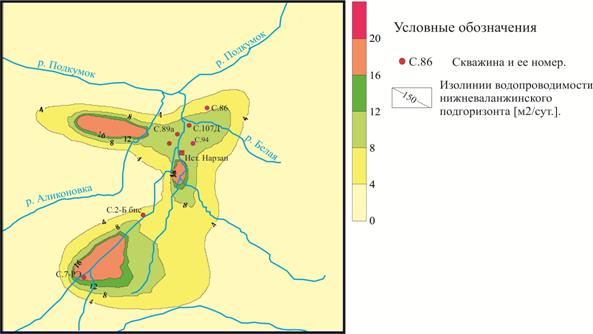
Для построения фильтрационной схемы использовались результаты ОФР, выполненных в разное время различными организациями [23,24]. Фильтрационные схемы (водопроводимости) нижнего валанжинского подгоризонта и титонского горизонта представлены на рис. 4.8. Упругая водоотдача валанжинских подгоризонтов принята равной 0,0001; гравитационная – 0,1. Упругая водоотдача титонского горизонта – 0,002. Рис. 4.8. Схемы распределения водопроводимости валанжинского и титонского горизотов.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 369. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
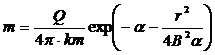
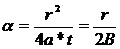
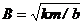; km – водопроводимость пласта; b – параметр перетекания. 
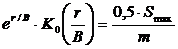(4.8).
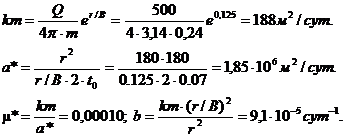
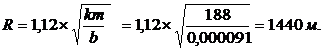
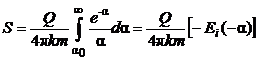(4.9),
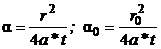; а* - пъезопроводность; r0, r – соответственно радиус скважины и радиус до точки наблюдения за динамикой понижения; t – текущее время от начала возбуждения скважины. 
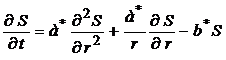(4.10),
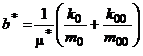; µ* - водоотдача пласта; k0, m0, k00, m00 – соответственно коэффициент фильтрации и мощность относительно водоупорных слоев в кровле и подошве пласта.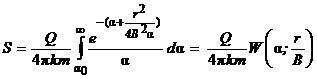 
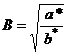– комплексный параметр.
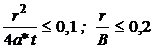(4.11),
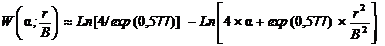(4.12).
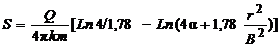(4.13).
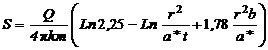, где b = k0/m0. 
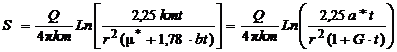(4.14). где 
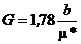.То есть, при наличии перетекания, процесс формирования понижения уровня в скважине аналогичен работе ее в изолированном пласте, с водоотдачей, изменяющейся по линейному закону.
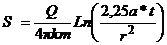, а при достаточно длительном времени (t®¥), преобразуется в известную формулу [4, 6]:
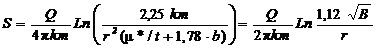(b = k0/m0).
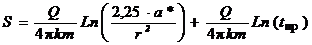. (4.15),
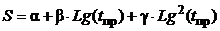(4.16),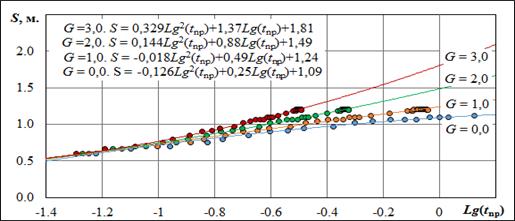
.
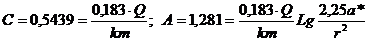