
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Глава 4. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ КИСЛОВОДСКОГОМЕСТОРОЖДЕНИЯ
4.1. Общие положения Упрощенная версия реального мира, выраженная с помощью математической символики, называется моделью. Построение моделей многие считают скорее искусством, чем теорией. Невозможно написать достаточно формализованную инструкцию, учитывающую все многообразие объектов, и, тем не менее, отсутствие точных правил не мешает широко использовать моделирование практически во всех научных областях. К настоящему времени уже накоплен значительный опыт, позволяющий сформулировать общие принципы и требования, которым должна удовлетворять модель. К ним можно отнести следующие: 1. Адекватность. Предусматривает соответствие модели целям исследования по уровню сложности и организации, а также соответствие реальному объекту относительно выбранного множества свойств и поставленной задаче. Модели, дающие максимально подробное описание системы, называют имитационными. Они используются в основном для целей чисто теоретического характера. Модели, описывающие основные внутренние механизмы, управляющие развитием системы в целом, называют качественными. С такими моделями приходится сталкиваться в большинстве случаев при решении конкретных задач. 2. Принцип минимизации размерности описания. Модели по своей природе всегда носят приближенный характер. Если в имитационной модели необходимо учитывать как можно больше деталей, то качественная модель, напротив, должна содержать их как можно меньше. Компромисс между этими требованиями определяется соотношением «точность/сложность». Минимизация описания достигается: - уменьшением числа переменных за счет исключения несущественных, или их объединением;  - изменением природы переменных параметров. Переменные параметры рассматриваются в качестве постоянных, дискретные - в качестве непрерывных; - изменением функциональных зависимостей между переменными: дискретные функции заменяются непрерывными, нелинейные представляются как линейные; - ограничением точности модели. Точность модели не может быть выше точности исходных данных. 3. Принцип верификации. По мере насыщения модели информацией адекватность ее меняется. Ряд факторов, никак не проявившихся на начальных этапах формирования модели и неучтенных в ее структуре, может привести к серьезным погрешностям. По этой причине приходится прибегать к периодическому чередованию процедур прогноза и проверки точности модели с последующей ее корректировкой, которая может осуществляться следующим образом: - по мере поступления информации структура модели не меняется, уточняются лишь коэффициенты модели; - по мере поступления информации производится изменение самой структуры модели, более точно отражающей внутренние механизмы функционирования объекта. 4. Блочное строение. Модели строятся по блочному принципу, которые выделяются по этапам и режимам функционирования системы. Такой подход существенно упрощает построение модели и все дальнейшие ее модификации. Перечисленные требования, являются общими, и не учитывают специфики объекта. В то же время специфичность объектов проявляется в любой отрасли и естественно закладывается в виде дополнительных принципов и требований, по которым формируется модель.
Согласно действующим рекомендациям основным методом подсчета эксплуатационных запасов для месторождений четвертой группы сложности является гидравлический. Особых возражений это положение не вызывает. Гидравлика базируется на фактически наблюдаемой динамике и химизме минеральных вод, и если ряды наблюдений достаточно представительны, то более достоверных данных, чем полученных экстраполяцией ретроспективы получить сложно. В то же время, гидравлический метод имеет ряд довольно существенных недостатков. Гидравлические методы требуют длительных натурных наблюдений, определяемых отрезками времени более года, не раскрывают физики процесса, соотношения баланса водных потоков и изменения их во времени. Да и методы прогнозирования минерализации оставляют желать лучшего. На эти вопросы дает ответ математическое моделирование. Однако и здесь существуют свои проблемы. Построение математической модели объекта, сама по себе, задача довольно сложная, требующая большого объема информации и более глубокого и детального изучения геолого-гидрогеологического строения объекта, знание емкостных и фильтрационных свойств, распределение их в пространстве, граничные условия в плане и разрезе, характер гидравлического взаимодействия отдельных водоносных горизонтов, миграционных параметров. Получение такой информации связано со значительными финансовыми вложениями, поскольку требуется постановка и проведение специальных опытно-фильтрационных и миграционных работ, хорошо поставленный гидрогеологический мониторинг, да и сама режимная сеть должна отвечать повышенным требованиям. Все это существенным образом ограничивает применение математических методов на месторождениях четвертой группы сложности, и без сомнения пока еще гидравлический метод остается доминирующим, и это бесспорно. В то же время, уровень компьютеризации, созданные пакеты прикладных программ, методов верификации математических моделей, общие тенденции развития его в других естественных научных дисциплинах однозначно свидетельствую о высокой эффективности метода. Уже в настоящее время на моделях прогнозируются популяции животных, климатические и метеорологические процессы, экологические системы. В этом отношении геологические науки не являются каким-то исключением. На начальных этапах изучения, особенно в сложных условиях, они выполняют вспомогательную роль, однако по мере насыщения информацией, адекватность моделей многократно возрастает, и с переходом на новый качественный уровень, роль математического моделирования может меняться. В любом случае, отказ от моделирования вообще это совершенно неверный подход, который не может быть оправдан сложностью объекта, или иными причинами. Несмотря на длительный срок эксплуатации Кисловодского месторождения, изученность его низка. В данном случае речь идет об изученности гидрогеологических параметров, пространственных закономерностях распределения емкостных и фильтрационных свойств, параметра перетекания. Режимная сеть расположена также крайне неудачно, в связи с чем, информативность ее оставляет желать лучшего. Кроме того, с 1991 г. эксплуатация месторождения осуществляется различными недропользователями, которые проходили экспертизу запасов в ГКЗ в различное время по своим подведомственным участкам. Полномочий на изучение этих участков другими недропользователями нет, что создает сложности в получении достоверной информации о динамике развития гидродинамических и гидрогеохимических процессов. По указанным причинам, моделированию в настоящей работе уделяется довольно скромная роль. Она заключается в основном как вспомогательный метод, дополняющий гидравлический, количественной оценке степени взаимодействия участков, в связи с вводом в эксплуатацию Северного фланга Центрального участка. Несмотря на длительность изучения и широкое использование гидравлических методов, единого мнения о взаимодействии участков в настоящее время нет. Во многом это объясняется коммерческими интересами, но все-таки, основная проблема заключается в дефиците гидрогеологической информации и несовершенстве, в том числе и гидравлических методов. Математические модели строятся на принципах сохранения энергии или баланса, чаще всего это так называемые динамические модели, в основе которых лежит описание объекта дифференциальными уравнениями с определяемыми по эмпирическим данным параметрами. Математические модели несравненно более трудоемки по сравнению с гидравлическими, требуют значительно большего объема информации и знаний об объекте, однако и преимущества их перед гидравлическими очевидны. Они довольно точно описывают физику геофильтрационного процесса, на их основе можно выполнять балансовые расчеты, прогнозировать динамику массопереноса. В общем случае система исходных дифференциальных уравнений, описывающих пространственный процесс фильтрации и массопереноса, при некоторых допущениях может быть представлена следующим образом [20, 21, 22, 23]:
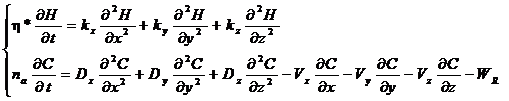
где: h* - упругоемкость пласта; kx, kx, kz – коэффициенты фильтрации по соответствующим координатам, Н - функция напора; nа -активная пористость; Dx, Dy, Dz – коэффициент гидродинамической дисперсии; С - концентрация исследуемого компонента; Vx,Vy,V,z – компоненты скорости фильтрации по соответствующим координатам; WR - параметр, характеризующий интенсивность внутрипластовых обменных процессов. Уравнения дополняются условиями однозначности, представляющими собой совокупность начальных и граничных условий. Если основными процессами, определяющими поглощение или потери солей из раствора, являются сорбция, ионный обмен, задержка солей в тупиковых порах и перетоки солей через кровлю и подошву пласта, то WR можно представить в следующем виде [23]:
N – количество солей, переходящих в твердую фазу и задерживающихся в тупиковых порах; Сn, Ck – концентрации солей поровых растворов солей в подошве и кровле соответственно; Dn, Dk – коэффициенты диффузии пород подошвы и кровли. Коэффициент диффузии является обобщенным параметром молекулярной (Dм) и конвективной диффузии или гидравлической дисперсии (Dг): D = Dм+ Dг. Коэффициент молекулярной диффузии в пористой среде Dм связан с коэффициентом молекулярной диффузии в свободном пространстве (жидкости) D0м: Dм = l1nD0м. (l1< 1,0). Коэффициент гидравлической дисперсии зависит от скорости фильтрации и внутренней структуры пористой среды: Dг = l2V. Уравнение кинетики сорбции в общем виде может быть выражено следующим образом [20]: где С, N – изменяющиеся во времени концентрации вещества в жидкой и твердой фазах; Cp, Np – равновесные концентрации. Применительно к грунтам кинетика сорбции описывается уравнением:
где a – кинетический коэффициент (константа скорости сорбции) [сут–1]; С – средняя концентрация в жидкой фазе в момент времени t; Ср – концентрация равновесия с количеством вещества N, поглощенным твердой фазой в данном месте. Связь между N и Ср определяется изотермой сорбции. При линейной изотерме Генри: Cp = bN (4.3), где b – коэффициент распределения вещества при сорбции. С учетом сказанного:
В тех случаях, когда сорбционное равновесие устанавливается очень быстро, кинетическая сорбция характеризуется уравнением:
Кинетическими уравнениями (4.2) – (4.5) могут быть также охарактеризованы и другие процессы поглощения или солеотдачи из раствора. Решение системы (4.1) представляется довольно затруднительным в виду сложности параметрической обеспеченности модели, и в первую очередь коэффициента kz. Пространственные модели могут с успехом использоваться в системах управления, когда прогнозирование на длительные периоды упреждения и особая точность решения не требуются. Однако при прогнозировании процессов на длительные сроки, в практических задачах значительно чаще рассматриваются плоско-пространственные модели. В общем случае, для условий геофильтрации флюидов, с учетом сорбции (десорбции), дисперсии, дифференциальные уравнения трансформируются к виду: где: m* - водоотдача пласта; bk, bn – параметр перетекания относительно водоупорного пласта, залегающего в кровле и подошве; Н – напор в изучаемом водоносном горизонте; Нk, Нn – напоры в смежных водоносных горизонтах: кровле и подошве соответственно; km – водопроводимость пласта; m – мощность водоносного горизонта; Vzn, Vzk – скорости перетекания воды через кровлю и подошву пласта соответственно; nэ – эффективная пористость. Эффективная пористость представляет собой: nэ = na+1/b; где b – коэффициент распределения при сорбции. Для инертных в отношении сорбции компонентов nэ = na. Для хорошо сорбируемых nэ > na, и может значительно превышать единицу. Как следует из (4.6) для решения задачи массопереноса требуется знание скорости фильтрации, и решение ее, осуществляется в два этапа. На первом решается задача геофильтрации в результате которой определяются скорости фильтрации и расходы потоков между центрами модельных блоков. На втором – собственно задача массопереноса. Решение выполняется численными методами. Это означает, что вместо дифференциальных уравнений в частных производных решается аналогичная система конечно-разностных уравнений, в которых дифференциалы искомой функции представлены в дискретной форме по координатам пространства и времени. Чтобы получить такую модель, исследуемая область разбивается равномерной или неравномерной сеткой на элементарные сопряженные блоки с шагом по пространственным координатам Dх и Dу, и все физические характеристики объекта в пределах выделенного блока, относят к его центру тяжести (узловой точке). То есть, вместо непрерывного изменения функции во времени и пространстве рассматриваются изменения ее в отдельных точках и через определенные дискретные моменты времени D t. В результате такого перехода получается система простых алгебраических уравнений относительно искомой функции, для решения которой используются разнообразные численные методы. В настоящее время известны явные, явно-неявные, неявные методы, позволяющие учитывать процессы перетекания и самые различные граничные условия. Они реализованы в многочисленных программах (Топаз, Plast, ModTech, МИФ-3 и др), и с позиций математики решение уравнений вида (4.1), (4.6) особой сложности не представляет. Более сложной задачей, как уже указывалось, является параметрическое обеспечение модели. Конечно, при ее формировании предварительная информация о фильтрационных свойствах среды имеется. Она определяется на основе полевых опытно-фильтрационных работ, которые проводятся в процессе геологического изучения объекта, однако это точечные оценки, которые не всегда совпадают со средними значениями, характеризующими процессы геофильтрации. В этой связи очень важно располагать методикой верификации, позволяющей по данным эпигноза производить корректировку параметров модели. То есть, имеющуюся информацию о режимах эксплуатации объекта за прошедшие периоды, воспроизводят на модели, и с помощью специальных приемов вводят корректировку параметров, обеспечивая максимальную сходимость фактических и модельных данных. Следует отметить, что в гидрогеологических исследованиях, в виду дороговизны, практически всегда приходится сталкиваться с дефицитом информации, в связи с чем совместно с геофизическими и опытно-фильтрационными исследованиями, широко используются методы интерполяции, математической статистики, многомерного регрессионного анализа, методики подбора. Методы подбора особенно эффективны в случаях, когда имеется ретроспективная информация, по которой можно внести корректировку в параметры модели. Конечно, он не отличается оригинальностью, но с развитием компьютерной техники, внедрение его в практику становится повсеместным, поскольку он представляет собой однотипный алгоритм очень просто реализуемый на вычислительных операциях.
|
||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 420. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

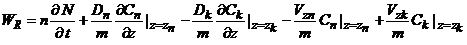 ,
,
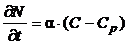 (4.2),
(4.2),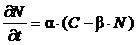 (4.4).
(4.4). 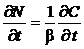 (4.5).
(4.5).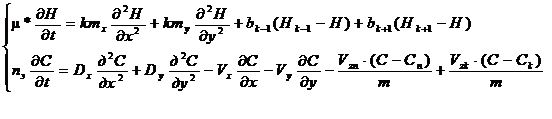 (4.6)
(4.6)