
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Свойства характеристических функций1) 2) 3) Если 4) Если 5) Если существует Примеры характеристических функций
с параметром
Пример 1.Пусть Решение.Характеристическая функция случайной величины
равна Характеристическая функция случайной величины
Тогда, используя свойства характеристических функций, получим
где Закон больших чисел. Неравенство Чебышева Пусть случайная величина
Теорема Чебышева Пусть случайные величины Тогда для любого
В частности, если все
Для биномиального распределения
Здесь  Пример 1.При изготовлении некоторой детали брак равен 5%. Оценить вероятность того, что при просмотре партии в 2000 штук выявляется отклонение доли бракованных деталей от установленного процента брака меньше чем на 1%. Решение.Воспользуемся формулой Здесь Тогда Пример 2.Сколько нужно произвести измерений, чтобы с вероятностью, равной 0,95, утверждать, что погрешность средней арифметической результатов этих измерений не превысит 0,1, если Решение.Воспользуемся формулой Здесь Имеем Квантили случайных величин Пусть непрерывная случайная величина Определение.Квантилью уровня
Рис. 4 Обозначим через через Свойства квантилей 1) 2) если 3) 4) 5) 6) для малых |
||||||||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 332. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
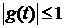 ,
, 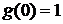 .
. , где
, где  – величина комплексно-сопряженная к
– величина комплексно-сопряженная к  .
. , то
, то  .
.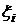 – независимые случайные величины с характеристическими функциями
– независимые случайные величины с характеристическими функциями 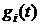 ,
,  и
и 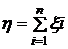 , то
, то  .
. , то
, то 

 Случайная величина
Случайная величина  распределена по биномиальному закону, тогда
распределена по биномиальному закону, тогда  ,
, 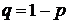 .
. , тогда
, тогда .
. , тогда
, тогда .
.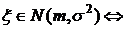
 .
.
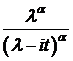 .
. – распределение Пирсона с n степенями свободы, то
– распределение Пирсона с n степенями свободы, то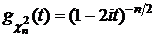 .
. принимает значения –1 и 1 с вероятностями
принимает значения –1 и 1 с вероятностями  каждое,
каждое,  имеет показательное распределение с параметром
имеет показательное распределение с параметром  .
.


 .
.


 (т.к.
(т.к.  то
то  ).
). ,
, характеристическая функция случайной величины
характеристическая функция случайной величины  .
. . Тогда для любого
. Тогда для любого  справедливо неравенство Чебышева
справедливо неравенство Чебышева или
или .
. независимы, существуют
независимы, существуют  ,
, 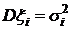 и
и  ,
,  ,
,  – некоторая постоянная.
– некоторая постоянная. .
.
 , то
, то .
. .
. в одном испытании,
в одном испытании,  – общее число испытаний,
– общее число испытаний,  – число испытаний, в которых событие
– число испытаний, в которых событие  ,
,  ,
,  ,
,  .
. .
. .
. .
. .
.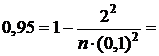
 ,
,  ,
,  .
. , плотность распределения –
, плотность распределения –  и пусть задано число
и пусть задано число 
 .
. случайной величины
случайной величины  , что
, что 
 .
.
 ;
; – квантиль уровня
– квантиль уровня  с
с  – квантиль уровня
– квантиль уровня  ,
,  ;
; квантиль уровня
квантиль уровня  , то
, то  ;
; при
при  ;
;

 ;
;

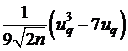
 .
.