
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ЛЕКЦИЯ 7. НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Непрерывная случайная величина – это переменная, которая может принимать любое значение в одном или нескольких заданных интервалах или в некоторых областях плоскости. Дадим более строгое определение. Определение 1. Случайная величина X – непрерывная случайная величина, если существует функция p(x) ³ 0, такая что, "xÎR, справедливо соотношение Ограничимся рассмотрением таких непрерывных случайных величин, для которых р(х) непрерывна всюду, кроме быть может, конечного числа точек. Определение 2.Функция p(х) называется плотностью распределения вероятностей непрерывной случайной величины.
Свойства непрерывной случайной величины 1. Доказательство вытекает из определения. 2. Плотность распределения p(x) определяет закон распределения непрерывной случайной величины
Это свойство также следует из определения плотности р(х). 3. Для любых х1 < х2 , Доказательство. По свойству функции распределения 4. Доказательство: 6. Вероятность того, что непрерывная случайная величина примет конкретное значение равна нулю, т.е. P(X = a) = 0. Доказательство. Событие A1 É A2 É…É An É…, Тогда, применив аксиому, получим
Из этого свойства следует, что Р(a<X<b) = P(a≤X<b) = P(a<X≤b) = P(a≤X≤b).
7. Если x – точка непрерывности p(x) и если Δ→0, то
Из этого свойства следует, что чем больше значение плотности p(x), тем больше вероятность попадания случайной величины в интервал (x; x + ∆).  Плотностью распределения может быть любая неотрицательная функция, интеграл от которой по всей числовой прямой равен 1, т.е. Функция распределения случайной величины любой точке xp ставит в соответствие вероятность р = F(xp) = P(X<xp), т.е. по xp найти F(xp). В иных случаях требуется решение обратной задачи ¾ по значению вероятности р найти решение уравнения F(xp) = р.
Определение 3. Точка xp, которая является решением записанного уравнения, называется квантилью,отвечающей заданному уровню вероятности р, или р % квантильюраспределения F(x). Из определения непрерывной случайной величины следует, что функция распределения непрерывной случайной величины непрерывна. Поэтому для непрерывной случайной величины для любого р, 0 < p < 1 существует квантиль хр.
Определение 4.Квантиль, отвечающая вероятности р = ½, называется медианой распределения. Медиана является одной из характеристик центра распределения случайных величин. Законы распределения непрерывных случайных величин Равномерное распределение Определение 5. Непрерывная случайная величина Х, принимающая значение на отрезке [a,b], имеет равномерное распределение, если плотность распределения имеет вид Нетрудно убедиться, что
Если случайная величина равномерно распределена, то вероятность того, что она примет значение из заданного интервала [x; x+∆] не зависит от положения интервала на числовой прямой и пропорциональна длине этого интервала
Покажем, что функция распределения Х имеет вид Пусть хÎ (–¥,a), тогда F(x) = Пусть хÎ [a,b], тогда F(x) = Пусть х Î (b,+¥], тогда F(x) = Найдем медиану x0,5. Имеем F(x0,5) = 0,5, следовательно
для равномерного распределения.
Рис. 1 |
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 172. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
. .
.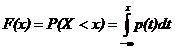 .
. .
. .
. .
. .
. можно представить как
можно представить как  . События An =
. События An =  a £ Х < a +
a £ Х < a + 
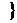 удовлетворят условиям аксиомы непрерывности
удовлетворят условиям аксиомы непрерывности .
. .
. .
. .
. . (1)
. (1)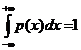 ,
,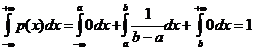 .
. .
. . (2)
. (2) .
. .
. = 0 +
= 0 +  .
. ,
,  . Итак, медиана равномерного распределения совпадает с серединой отрезка [a, b]. На рис.1 приведен график плотности р(х) и функции распределения F(x)
. Итак, медиана равномерного распределения совпадает с серединой отрезка [a, b]. На рис.1 приведен график плотности р(х) и функции распределения F(x)