
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основные свойства функции распределения1. Функция распределения принимает значения из промежутка [0, 1], т.е.
0 ≤ F(x) ≤ 1.
Это свойство следует из определения функции распределения. 2. Если х2 >х1, то 3. P(x1≤X<x2 ) = F(x2)-F(x1). (1)
Доказательство. Представим событие, состоящее в том, что случайная величина примет значение, меньшее х2, в виде суммы несовместных событий –
{w: X(w) < x2} = {w: X(w)< х1} È {w: x1 ≤ X(w) < x2}.
Так как события несовместные, применим аксиому 3 –
P(X < x2) = P(X < x1) + P(x1 ≤ X < x2),
но P(X < x2) = F(x2), P(X < x1 ) = F(x1), следовательно
F(x2) = F(x1) + P(x1 ≤ X < x2), (2)
а это и означает, что P(x1≤X<x2 ) = F(x2)–F(x1).
4. Функция распределения – неубывающая функция, т.е. если x2 > x1 => F(x2) ≥ F(x1).
Доказательство. Если x2 > x1, то справедливо соотношение (2). Но, согласно
аксиоме 1 P(x1 ≤ X < x2) ≥ 0, следовательно, F(x2) ≥ F(x1).
5. P(X ≥ x ) = 1-F(x).
Доказательство. События {w: X(w) ≥ x} и {w: X(w) < x} – противоположные события, так как они несовместные и
{w: X(w) ≥ x}È{w: X(w) < x} = Ω, следовательно,
Р{w: X(w) ≥ x} + Р{w: X(w) < x}=1, тогда Р(X(w) ≥ x) = 1–Р(X(w) < x) = 1 – F(x).
6. Если х ® ¥, то
Доказательство. Пусть x1, …, xn …– бесконечно возрастающая числовая последовательность, xn → ∞ при n → ∞, надо доказать, что Рассмотрим последовательность несовместных событий А1, А2, …, Аn, …
А1 = {w: X(w)<x1}, А2 = {w: x1 ≤ X(w) < x2}, …, An = {w: xn-1 ≤ X(w) < xn}, n = 3, 4, … 
Очевидно, что событие {w: X(w) < xn} можно представить в виде суммы событий А1, А2, …, Аn {w: X(w) < xn}= Так как события Ai несовместны, то по аксиоме сложения
Легко видеть, что событие, равное сумме всех событий Аi, является достоверным событием, т.е.
Тогда по аксиоме 2 и аксиоме 3` имеем
Замечание. Мы не пишем 6. Если x → - ∞, то F(x) → 0. 7. Функция распределения непрерывна слева, т.е. Свойства 6, 7 можно доказать при помощи аксиомы непрерывности, которая является альтернативной по отношению к аксиоме 3`. То есть в аксиоматику теории вероятностей вместо аксиомы 3` можно включить аксиому непрерывности, тогда аксиому 3` можно будет доказать как теорему и наоборот, аксиому непрерывности можно доказать с использованием аксиомы 3`. Аксиома непрерывности. Пусть A1, A2, .., An, … – последовательность событий из S, причём A1 Доказательствосвойства 6. Рассмотрим произвольную бесконечно убывающую монотонную последовательность
x1 > x2 >…> xn >…, причём xn→-∞, n→∞.
Рассмотрим последовательность событий A1, … , An, …, Аn ={w: (Х < хn )}. По определению Р(Аn) = Р(Х< хn) = F(хn). Очевидно, что последовательность событий A1, A2, ..., An удовлетворяет условиям аксиомы непрерывности: A1 Тогда,
График функции распределения F(x) изображен на рис.1.
Рис.1. Приведем доказательство аксиомы непрерывности. Пусть даны события A1, A2, ...,An, … и A1 Тогда, перейдя к противоположным событиям, получим Представим события
Убедиться в правильности этих равенств можно при помощи диаграмм Эйлера–Вена. Используя расширенную аксиому сложения, получим
Р( = =
Следовательно, Р( =1–
|
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 167. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 .
. .
. .
. .
. = Ω.
= Ω. .
. , так как не определен предельный переход под знаком вероятности.
, так как не определен предельный переход под знаком вероятности.
 .
. A2
A2  , тогда
, тогда  .
. .
. , следовательно
, следовательно
 .
.
 1 Ì
1 Ì  n =
n =  .
.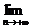 ( Р(
( Р(  , т.е. получили, что
, т.е. получили, что