
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Фотоэлектрическое поглощение.Суть фотоэффекта заключается в передаче энергии фотона одному из атомных электронов с вылетом последнего из атома с кинетической энергией равной Ее=Е/γ -ЕK , либо Ее=Еγ / -ЕL, , где ЕK, ЕL – энергия связи электронов , находящихся на К, L и т.д. оболочках атома. При этом предполагается, что энергия отдачи атома пренебрежимо мала. Энергия связи электронов, находящихся на К-оболочке, для разных элементов находится в диапазоне от 10 до 140 кэВ, на L-оболочке не превышает 30 кэВ, поэтому фотоэффект характерен для фотонов с низкой энергией. Образующиеся свободные электроны с энергией ниже энергии покоя (0,511 МэВ) вылетают из атома преимущественно в направлении перпендикулярном направлению движения первичного фотона, с ростом энергии их угловое распределение вытягивается в направлении первичного фотона, однако никогда с ним не совпадает. Необходимо отметить, что фотоэффект не возможен на свободном электроне; из законов сохранения энергии и импульса требуется наличие третьего тела, каким выступает атом, хотя на балансе энергии это практически не сказывается. Такое заключение можно подтвердить следующим образом. Законы сохранения энергии и импульса при полном поглощении фотона электроном можно записать в виде: Еγ/ + mc2 = mc2/ где Еγ/, | 
Рис.3.3. Сечения фотоэффекта для кислорода, меди и свинца
С наибольшей вероятностью это явление происходит при равенстве энергии фотона энергии электрона, находящегося на соответствующей оболочке. С ростом энергии фотона сечение фотоэффекта резко снижается примерно пропорционально Е/γ-7/2, при Е/γ>>ЕK оно становится обратно пропорциональным Е/γ. Учитывая резкий спад сечения фотоэффекта при энергии фотонов ниже энергии соответствующего уровня, для фотонов с энергиями Е/γ >ЕK вклад К-оболочки в полное сечение фотоэффекта составляет не менее 80%. Качественно при энергиях фотонов 0,511 МэВ > Е/γ > ЕK зависимость сечения фотоэффекта на К-оболочке можно описать формулой Гайтлера:
τК=32
в которой rе=2,82*10-15м – классический радиус электрона, Z – атомный номер вещества, на котором происходит фотоэффект. При энергиях фотонов Еγ/ >> 0,511 МэВ это сечение описывается приближенной формулой Заутера: τК=4πrе2(mc2)Z5/(137*Eγ/) (3.19).
Из формул видно, что фотоэффект играет существенную роль при низких энергиях фотонов и для тяжелых материалов, возрастая с ростом атомного номера как Z5. Энергия первоначального фотона при фотоэффекте разделяется на кинетическую энергию образующегося электрона и энергию ионизации, равную энергии электрона, находящегося на соответствующей оболочке. Последняя затем реализуется в виде энергии фотона, испускаемого при переходе электрона с ниже лежащей электронной оболочки атома на освободившуюся. Это позволяет сечение фотоэффекта представить в виде двух составляющих: τ = τe + τγ (3.20), где τe - характеризует часть сечения фотоэффекта, приводящую к преобразованию первичной энергии фотона в кинетическую энергию электрона. τγ - характеризует преобразование энергии первичных фотонов в энергию характеристического излучения. Комптоновское рассеяние. Комптоновское рассеяние рассматривается как процесс упругого рассеяния фотона с энергией Еγ/ на свободном электроне, при котором изменяется энергия Еγ/→Еγ и направление движения первичного фотона
Рис.3.4. Схема комптоновского рассения
Из законов сохранения энергии и импульса при упругом столкновении фотона на покоящемся электроне, записанных в виде соотношений: Еγ/ + mc2 = Еγ + mc2/ вкоторых Еγ/,
Еγ=Еγ/ / [ 1+(Eγ//mc2)*(1-Cosθs)] (3.22).
Из формулы (3.22) следует, что при рассеянии фотона прямо вперед (θs=0) энергия фотона не меняется (Еγ=Еγ/), а при рассеянии назад (θs=π) энергия рассеянного фотона будет минимальна (Еγ = Еγ//(1+3,91Еγ/), но не меньше 0,255 МэВ независимо от первоначальной энергии фотона. Если энергия фотона Еγ/<< mc2 , то вторым членом в знаменателе формулы (3.22) можно пренебречь по сравнению с единицей, и тогда при любом угле рассеяния θs комптоновское рассеяние происходит без передачи энергии фотона электрону. Этот эффект приводит к накоплению рассеянных фотонов при прохождении в легких средах, когда комптоновское рассеяние является преобладающим эффектом взаимодействия. Переходя к безразмерным энергетическим переменным ε=Е/mc2 и обозначив μs=Сos θs , формулу (3.22) можно записать в виде:
ε = ε//[1+ ε/(1- μs)] (3.23),
который часто используется в практических расчетах. Полное микроскопическое поперечное сечение комптоновского рассеяния на свободном электроне, полученное Клейна-Нишины-Таммом из квантовой электродинамики, описывается формулой: σ(ε/)=2πre2 результаты расчетов по которой приведены на рис.3.5.
Рис.3.5. Зависимость полного и парциальных микроскопических поперечных сечений комптон эффекта от энергии фотонов.
Приведенная на рис.3.5 зависимость микроскопического поперечного сечения комптоновского рассеяния от энергии фотонов показывает, что при энергиях фотонов больших примерно 5 МэВ оно уменьшается обратно пропорционально энергии, при меньших энергиях до примерно 0,05 МэВ зависимость имеет вид σ ~1/ В зависимости от атомного номера материала полное микроскопическое поперечное сечение комптон-эффекта в расчете на 1 атом пропорционально числу электронов в атоме Z и вычисляется для данного материала умножением σ (ε/) на Z. Дифференциальное микроскопическое поперечное сечение комптоновского рассеяния, определяющее вероятность фотону с энергией dσ(ε/,θs)/dΩ=
Рис.3.6. Дифференциальное микроскопическое эффективное поперечное сечение комптоновского рассеяния.
Из приведенных на рис.3.6 данных по угловому распределению рассеянных фотонов видно, что при низких энергиях фотонов их угловое распределение близко к изотропному; с ростом энергии анизотропия увеличивается и высокоэнергетичные фотоны при рассеянии летят преимущественно вперед. При начальной энергии фотона 10 МэВ доля обратно летящих рассеянных фотонов не превышает 1%. Дважды дифференциальное эффективное микроскопическое поперечное сечение комптоновского рассеяния может быть получено, используя выражение (3.25) и формулу (3.23), указывающую однозначную зависимость энергии рассеянного фотона от угла рассеяния:
dσ(ε/ → ε , μs )/dΩdE= = С точки зрения переноса энергии фотонами комптон-эффект представляет собой процесс частичного рассеяния и частичного поглощения энергии в той ее части, которая передается электрону. Показателем передаваемой электрону энергии фотона служит средняя относительная потеря фотоном энергии при комптоновском рассеянии: Используя эту величину, вводят понятия сечения комптоновского поглощения: а и сечение истинного комптоновского рассеяния
s
На рис. 3.5 приведены зависимости этих парциальных сечений от энергии фотонов, из которых видно, что при низких энергиях фотонов передача энергии фотона электрону мала, а при энергиях выше 1,6 МэВ с ростом энергии фотонов все большая часть энергии фотона переходит в кинетическую энергию электрона. Описанные выше закономерности взаимодействия фотонов с электроном при комптоновском рассеянии рассматривают рассеяние фотона на электроне, свободном от связи с другими частицами. Это справедливо только при условии, что импульс, передаваемый электрону, намного превышает импульс его первоначального движения в атоме, т.е. λе> >λ / Sin (θs /2), где l и lе ‑ первоначальные длины волн соответственно фотона и электрона. Наличие связей и первоначального движения электронов приводит к уменьшению вероятности комптоновского рассеяния и исчезновению жёсткого соотношения между ε/, ε и qs (так называемый «binding» эффект). В этом случае дифференциальное микроскопическое поперечное сечение комптоновского взаимодействия можно рассчитать, введя поправку к распределению Клейна–Нишины-Тамма (формула (3.26):
dσс (ε/ → ε , μs ) / dΩ dE = I(Z,v(μs , ε/)) dσ(ε/ → ε , μs ) / dΩ dE (3.30),
Рис.3.7. Нерелятивистская функция рассеяния Хартри‑Фока. Параметр ν – обратная длина волны фотона определяется по формуле ν = Sin(θs/2)/λ=кε/ В отличие от распределения формулы (3.26) в формуле (3.30) появляется зависимость от материала рассеивателя. Эффект учета связи электронов, приводит к уменьшению вероятности рассеяния вперёд (к полному запрету рассеяния по направлению первоначального движения фотона) и к некоторому увеличению вероятности рассеяния относительно первоначального движения g ‑ кванта для небольших энергий и более тяжелых элементов назад. Функция I(Z,v(μs, ε/)) табулирована для разных элементов. |
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 461. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 (3.17),
(3.17), |=Eγ/ / c -энергия и импульс фотона до поглощения,
|=Eγ/ / c -энергия и импульс фотона до поглощения,  –скоростьэлектрона после взаимодействия, mc2 – масса покоя электрона, β=v/с. Из указанных соотношений следует, что они могут выполняться только при условии, что скорость электрона после взаимодействия будет равна скорости света, чего для частицы с ненулевой массой невозможно, поэтому для уравновешивания импульсов необходимо третье тело, которым выступает атом. Фотоэффект – типично резонансное явление. На рис. 3.3 для примера приведены сечения фотоэффекта для разных материалов.
–скоростьэлектрона после взаимодействия, mc2 – масса покоя электрона, β=v/с. Из указанных соотношений следует, что они могут выполняться только при условии, что скорость электрона после взаимодействия будет равна скорости света, чего для частицы с ненулевой массой невозможно, поэтому для уравновешивания импульсов необходимо третье тело, которым выступает атом. Фотоэффект – типично резонансное явление. На рис. 3.3 для примера приведены сечения фотоэффекта для разных материалов.
 πrе2(mc2)7/2Z5/(3*1374*E/γ 7/2) (3.18),
πrе2(mc2)7/2Z5/(3*1374*E/γ 7/2) (3.18), , но он не исчезает (Рис.3.4.).
, но он не исчезает (Рис.3.4.).
 (3.21),
(3.21), -энергия и импульс фотона до и после рассеяния соответственно, (|
-энергия и импульс фотона до и после рассеяния соответственно, (|  (3.24)
(3.24)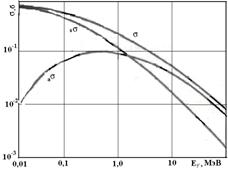
 .
.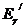 после рассеяния на электроне полететьпод углом θs относительно направления движения первичного фотона, показано на рис.3.6 и описывается формулой:
после рассеяния на электроне полететьпод углом θs относительно направления движения первичного фотона, показано на рис.3.6 и описывается формулой:
 (3.25)
(3.25)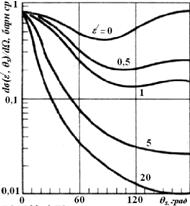
 (3.26).
(3.26).
 =
=  (3.27).
(3.27). =
=  где I(Z,v(μs , ε/)) ‑ соответствующая нерелятивистская функция рассеяния Хартри‑Фока, учитывающая эффект связи электронов (рис.3.7).
где I(Z,v(μs , ε/)) ‑ соответствующая нерелятивистская функция рассеяния Хартри‑Фока, учитывающая эффект связи электронов (рис.3.7). , в которой к=10-8 mc2/(h
, в которой к=10-8 mc2/(h