
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Модуль числа. Решение уравнений, содержащих переменную под знаком модуляГеометрический смысл модуля: Аналитически его определяют так: Если под знаком модуля стоит неотрицательное выражение, то знак модуля можно опустить и выражение, стоящее под знаком модуля, записать без изменения. Если под знаком модуля стоит отрицательное выражение, то знак опустив модуля, выражение, стоящее под знаком модуля, взять в скобки и перед ним поставить знак «минус». Основные свойства модуля: 1. 5. Используя геометрический смысл модуля и его определение получают способы решения уравнений с модулем. I тип уравнений
1) если 2) если 3) если
Таких точек две. Т.о. при Вернемся к уравнению (1). Наиболее рационально его решать таким же подходом. Т.е. 1) если 2) если 3) если II тип уравнений Решать это уравнение можно несколькими способами: 1–й способ – используя определение модуля: 2–й способ – используя подход как к уравнениям I типа: Замечание:1–й и 2–й способ в решении таких уравнений выбирают в зависимости от того, какое неравенство 3–й способ – метод интервалов: 1) находим критические точки:  2) наносим полученные значения на числовую ось ; 3) определяем знаки 4) рисуем кривую знаков; 5) решаем уравнение на каждом промежутке в отдельности, раскрывая модуль согласно рисунку; 6) ОДЗ. Если это не вся числовая ось, учитываем сразу на рисунке после того как нарисовали кривую знаков. III тип уравнений Уравнения содержат несколько модулей: 1–й способ –можно использовать определение модуля и рассматривать 4 случая возможных знаков 2–й способ – метод интервалов: рисуем столько числовых осей и кривых знаков, сколько модулей в уравнении. IV тип уравнений 1–й способ –решаем совокупность уравнений: 2–й способ – метод интервалов. 3–й способ – используя теорему равносильности: если обе части уравнения Это значит, что корни те же или оба не имеют корней. Поэтому уравнение (4) равносильно уравнению: Далее используем свойство квадрата модуля: V тип уравнений Это уравнения, решаемые заменой переменной. Например: Вводим замену VI тип уравнений Уравнения, решение которых основано на свойствах модуля 1. 4. 7.
Модуль числа. Решение неравенств, содержащих переменную под знаком модуля Опр. |f(x)|=f(x), x>0 – модуль функции. –f(x), x<0 а , если а ≥ 0, – модуль числа Определение: l а l= –а, если а<0. Решение неравенств, содержащих переменную под знаком модуля |
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 323. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 – расстояние от точки 0 до точки
– расстояние от точки 0 до точки  на числовой прямой. Модуль называют еще абсолютной величиной.
на числовой прямой. Модуль называют еще абсолютной величиной.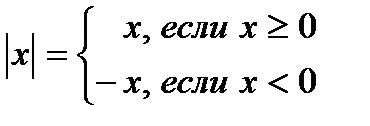 .
. ; 2.
; 2. 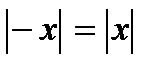 ; 3.
; 3. 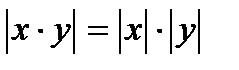 ; 4.
; 4.  ;
; ; 6.
; 6.  ; 7.
; 7.  ; 8.
; 8. 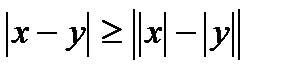 .
. , где
, где  число (1), Рассмотрим частный случай:
число (1), Рассмотрим частный случай: 
 , то решений нет;
, то решений нет; , то единственное решение
, то единственное решение 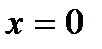 ;
; , то геометрически это означает, что надо найти такие точки на числовой оси, которые находятся на расстоянии в
, то геометрически это означает, что надо найти такие точки на числовой оси, которые находятся на расстоянии в 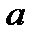 масштабных единиц от точки 0.
масштабных единиц от точки 0.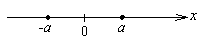
 .
. ;
; .
. (2), где
(2), где  некоторые выражения с переменной.
некоторые выражения с переменной.
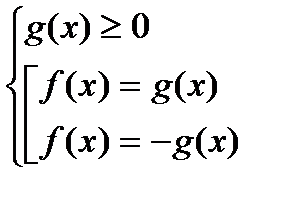
 или
или 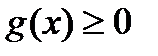 решается легче.
решается легче.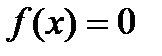 ;
; для каждого из полученных интервалов;
для каждого из полученных интервалов;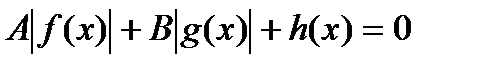 , (3), где
, (3), где  .
.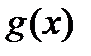 . Этот способ, как правило, не является рациональным.
. Этот способ, как правило, не является рациональным. , (4), где
, (4), где  .
. .
. , где
, где  при всех значениях
при всех значениях  , то получится уравнение
, то получится уравнение  , равносильное данному.
, равносильное данному.

 , (5)
, (5) . Решаем квадратное уравнение относительно новой переменной. Затем, возвращаясь к замене, получаем совокупность уравнений I–го типа:
. Решаем квадратное уравнение относительно новой переменной. Затем, возвращаясь к замене, получаем совокупность уравнений I–го типа:  .
. . 2.
. 2.  . М 3.
. М 3. 
 5.
5.  6.
6.  .
. . 8.
. 8.  .
.