
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Абсолютная сходимость влечет сходимость.То есть, если сходится интеграл от модуля подынтегральной функции
При использовании второго признака сравнения часто возникают интегралы вида Необходимо помнить:
Пример. Исследовать сходимость. Исследуем характер поведения функции на бесконечности. Рассмотрим функцию
Тогда порядок поведения функции на бесконечности определяется выражением
Напомним, что мы можем пренебречь любым конечным отрезком. Рассмотрим функции Имеем, Рассмотрим
= Следовательно, по второму признаку сравнения, оба интеграла сходятся.
Пример.Исследовать сходимость Для исследования сходимости данного интеграла в начале исследуем сходимость интеграла от модуля подынтегральной функции Рассмотрим
Следовательно, несобственный интеграл
В заключение сделаем еще два замечания, касающиеся несобственных интегралов первого рода. 1.Несобственный интеграл вида 2.Несобственный интеграл, у которого оба предела интегрирования бесконечны ( При этом несобственный интеграл 
Пример. Вычислить несобственный интеграл или доказать его расходимость Решение. (Мы выбрали Исследуем отдельно каждый из интегралов в правой части.
Следовательно
Пример. Вычислить несобственный интеграл или доказать его расходимость Решение.
Этот интеграл является расходящимся, и нет никакой необходимости исследовать второй интеграл. Можно сразу сделать вывод, что
Несобственные интегралы второго рода.
До настоящего момента, при вычислении определенного интеграла, мы считали, что подынтегральная функция является непрерывной на всем отрезке, и как следствие этого, ограниченной. Несобственные интегралы второго рода возникают в тех случаях, когда функция не является непрерывной на отрезке интегрирования. Пусть функция В этом случае для любого Несобственный интеграл
При этом, если указанный предел существует, то несобственный интеграл Если Если функция
Если функция
При этом исходный интеграл называется сходящимся, если сходится каждый из интегралов в правой части соотношения. Если хотя бы один из них расходится, то и исходный интеграл называется расходящимся. Наконец, если функция
При этом, если хотя бы один из интегралов в правой части является расходящимся, то и весь интеграл считается расходящимся. Ниже будут сформулированы свойства и признаки сходимости несобственного интеграла второго рода. При их формулировке мы будем предполагать, что функция Опять полезно учитывать, что вопрос сходимости или расходимости несобственного интеграла первого рода определяется поведением подынтегральной функции в окрестности точки Для несобственных интегралов от неотрицательных функций важную роль играют признаки сравнения, которые мы сформулируем ниже. Первый признак сравнения. Пусть имеются непрерывные при Тогда, 1) если 2) если
Второй признак сравнения. Пусть имеются непрерывные при Для несобственных интегралов от знакопеременных функций часто бывает полезен следующий факт. |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 176. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , то сходится интеграл от самой этой функции
, то сходится интеграл от самой этой функции  .
. , где
, где  .
. ;
; . (Докажите самостоятельно непосредственным вычислением)
. (Докажите самостоятельно непосредственным вычислением)  .
. . При больших значениях
. При больших значениях 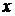 имеем
имеем .
. .
. и
и  .
. сходится, так как
сходится, так как 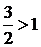 .
.
 .
.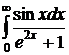 .
. . Поскольку
. Поскольку  , то
, то  .
. .
. .
. , то, и силу первого признака сравнения,
, то, и силу первого признака сравнения,  определяется аналогичным образом, а именно
определяется аналогичным образом, а именно 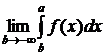 .
. ), определяется равенством
), определяется равенством .
.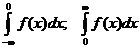 ) в правой части. Если хотя бы один из этих интегралов расходится, то
) в правой части. Если хотя бы один из этих интегралов расходится, то  .
. .
. , но могли взять и любое другое число, например ноль.)
, но могли взять и любое другое число, например ноль.)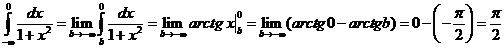 .
. .
. .
. .
. .
.
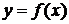 непрерывна на полуинтервале
непрерывна на полуинтервале  , а в точке
, а в точке  имеет особенность. (Например,
имеет особенность. (Например,  .)
.)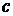 существует определенный интеграл
существует определенный интеграл 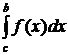 .
. определим следующим образом:
определим следующим образом: .
. , а в точке
, а в точке  имеет особенность, то несобственный интеграл
имеет особенность, то несобственный интеграл 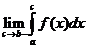 .
. , а в точках
, а в точках  имеет особенности, то несобственный интеграл
имеет особенности, то несобственный интеграл 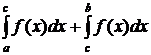 , где
, где  имеет особенности в точках
имеет особенности в точках  , где
, где  , то несобственный интеграл
, то несобственный интеграл  .
. для любых
для любых  .
. функции
функции  . При этом
. При этом  при
при  тоже сходится, при этом
тоже сходится, при этом  .
.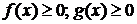 при
при  . Тогда либо оба интеграла
. Тогда либо оба интеграла