
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Отметим, что при замене переменной меняется не только подынтегральное выражение, но и пределы интегрирования.Стр 1 из 4Следующая ⇒ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
Московский государственный университет Приборостроения и информатики
Кафедра высшей математики ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ (решение задач) Учебное пособие для студентов всех форм обучения для самостоятельной подготовки к выполнению контрольных работ.
Москва 2005
Составитель: к.ф.м.н., доцент Выборнов А.Н..
В пособии рассмотрено понятие определенного интеграла, методы вычисления определенных интегралов, а также несобственные интегралы, геометрические и механические приложения определенных интегралов. Пособие составлено на основе пособия МГУПИ для заочного отделения (авторы: Баланкина Е.С., Головешкин В.А., Каримова Н.А., Меренкова Т.В., Соркина Л.И., Якобовская И.М.) Составителем отредактировано изложение теоретических положений и некоторых методов решения задач. Пособие может использоваться как дополнительное пособие по развитию навыков решения задач.
Прежде чем перейти к непосредственному решению примеров, напомним некоторые факты теоретического курса. Начнем с самого понятия определенного интеграла.
Фиг.1
Пусть на отрезке Обозначим  Теперь перейдем к более строгим рассуждениям. Назовем интегральной суммой Заметим, что значение интегральной суммы зависит и от способа разбиения и от способа выбора точек
Определение. Если существует предел интегральных сумм при Таким образом Возникает естественный вопрос, а существуют ли вообще такие функции, для которых это понятие имеет смысл. Мы не будем приводить доказательство, а просто сформулируем известный факт: «Всякая функция, непрерывная на отрезке, является интегрируемой по этому отрезку». (Отметим, что непрерывными функциями не исчерпывается класс интегрируемых функций.) Сформулируем свойства определенного интеграла. При формулировке свойств мы будем предполагать, что речь идет о функциях, интегрируемых по отрезку. 1. 2. 3. Кроме того, по определению полагают
Далее перейдем к формуле Ньютона-Лейбница, которая устанавливает связь между неопределенным и определенным интегралом. Пусть функция Тогда
- это соотношение и называется формулой Ньютона-Лейбница . Символически это часто записывается следующим образом Если Запись
Следовательно, при известной первообразной вычисление определенного интеграла не должно представлять принципиальных затруднений, если не считать, конечно, таковыми подстановку чисел в известную формулу.
Найти. (Мы использовали то, что функция Приведем еще два метода, которые используются достаточно часто при вычислении определенных интегралов.
Формула интегрирования по частям.
Напомним, что в случае неопределенного интеграла формула интегрирования по частям записывалась в виде Для определенного интеграла имеем Формула замены переменной. Пусть требуется вычислить Тогда Отметим, что при замене переменной меняется не только подынтегральное выражение, но и пределы интегрирования. Далее перейдем к решению задач.
Пример. Вычислить Найдем первообразную функции
Отметим, что при вычислении определенного интеграла значение произвольной постоянной не играет роли, поэтому мы положили ее значение равным нулю. Тогда = На всякий случай, напомним: 1) Пример. Вычислить При решении этого примера воспользуемся методом интегрирования выражений вида
= Следовательно Пример. Вычислить При решении этого примера воспользуемся методом интегрирования выражений вида Сделает замену переменных Следовательно, = Пример. Вычислить Воспользуемся методом интегрирования выражений вида Определим новые пределы интегрирования: Следовательно Пример. Вычислить Данный интеграл перепишем в виде Следовательно Выражение
Приводя левую и правую части к общему знаменателю и, отбрасывая его, получаем
Для определения неизвестных коэффициентов получаем систему уравнений
Решая эту систему, получаем Тогда
Следовательно
= Пример. Сделаем замену переменной Получаем
= (Мы воспользовались: 1) формулой суммы кубов Пример. Вычислить Воспользуемся формулой интегрирования по частям. Пусть Получаем
Воспользуемся еще один раз формулой интегрирования по частям: Имеем
=
=
Пример. Вычислить Воспользуемся формулой интегрирования по частям. Пусть
Получаем
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ Рассматриваются два типа несобственных интегралов – несобственные интегралы первого и второго рода. К несобственным интегралам первого рода относят интегралы с бесконечными пределами интегрирования. Поясним суть этого понятия. Пусть функция Рассмотрим
Пример. Вычислить несобственный интеграл или доказать его расходимость Решение. =
Пример. Вычислить несобственный интеграл или доказать его расходимость Решение. Воспользуемся формулой интегрирования по частям.
= Пример. Вычислить несобственный интеграл или доказать его расходимость Решение.
Следовательно, данный интеграл расходится. При исследовании несобственных интегралов первого рода очень часто основную роль играет вопрос, сходится ли данный интеграл или он расходится. В решении этого вопроса полезно учитывать, что вопрос сходимости или расходимости несобственного интеграла первого рода определяется поведением подынтегральной функции на бесконечности. Это означает, что любой конечный отрезок влияет лишь на значение интеграла, но не влияет на вопрос его сходимости. То есть при исследовании сходимости интеграла Для несобственных интегралов от неотрицательных функций важную роль играют признаки сравнения, которые мы сформулируем ниже. Первый признак сравнения. Пусть имеются непрерывные при Тогда, 1) если
2) если
Второй признак сравнения. Пусть имеются непрерывные при
Для несобственных интегралов от знакопеременных функций часто полезен следующий факт. |
|||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 239. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |



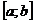 задана функция
задана функция 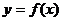 . Разобьем отрезок
. Разобьем отрезок  частей (фиг.1) точками
частей (фиг.1) точками  (
( 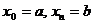 ).
). 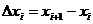 , где
, где 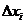 - длина отрезка
- длина отрезка 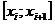 . На отрезке
. На отрезке 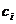 . Вычислим значение функции
. Вычислим значение функции 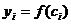 . Интуитивно понятно, что величина
. Интуитивно понятно, что величина 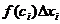 при малом значении
при малом значении 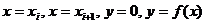 . Тогда сумма таких площадей по всем отрезкам разбиения
. Тогда сумма таких площадей по всем отрезкам разбиения 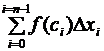 будет близка к площади криволинейной трапеции, ограниченной линиями
будет близка к площади криволинейной трапеции, ограниченной линиями 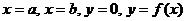 .
.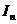 сумму вида
сумму вида 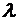 , где
, где 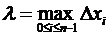 .
.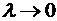 , и этот предел не зависит ни от способа разбиения, ни от способа выбора точек
, и этот предел не зависит ни от способа разбиения, ни от способа выбора точек 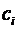 , то функция
, то функция 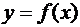 называется интегрируемой на отрезке
называется интегрируемой на отрезке 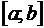 , а значение предела называется определенным интегралом от данной функции по отрезку
, а значение предела называется определенным интегралом от данной функции по отрезку 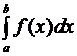 .
.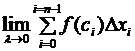 .
. , где А – постоянная величина.
, где А – постоянная величина.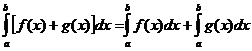 .
.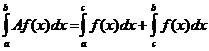 .
.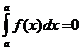 .
. при
при 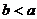 .
.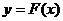 является первообразной для функции
является первообразной для функции 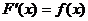 .
.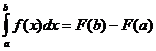
 .
.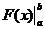 -читается «эф от икс в подстановке от а до бэ», а математически эта подстановка означает
-читается «эф от икс в подстановке от а до бэ», а математически эта подстановка означает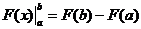 .
.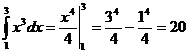 .
.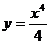 является первообразной для функции
является первообразной для функции 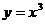 .)
.)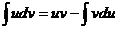 .
. .
.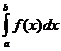 и сделана замена переменной интегрирования
и сделана замена переменной интегрирования 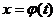 , где
, где 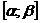 , имеющая непрерывную производную на этом отрезке.
, имеющая непрерывную производную на этом отрезке.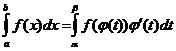 .
.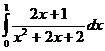
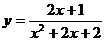 . При ее вычислении воспользуемся методом интегрирования выражений, содержащих квадратный трехчлен в знаменателе.
. При ее вычислении воспользуемся методом интегрирования выражений, содержащих квадратный трехчлен в знаменателе.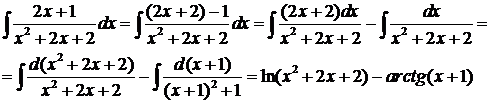
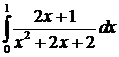 =
= 
 .
.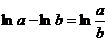 ; 2)
; 2) 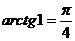 .
.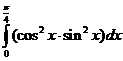 .
.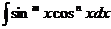 в случае, когда оба показателя степени четные.
в случае, когда оба показателя степени четные.
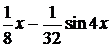 .
.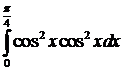 =
= 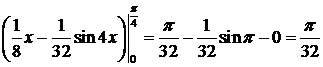 .
. .
.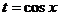 . Тогда
. Тогда  ,
, 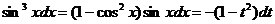 . Определим новые пределы интегрирования. Имеем:
. Определим новые пределы интегрирования. Имеем:  ,
, 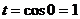 ;
; 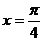 ,
, 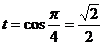 .
.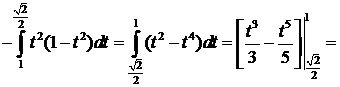
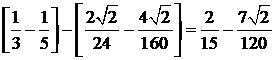 .
.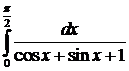 .
. и сделаем замену переменной
и сделаем замену переменной 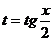 . Тогда
. Тогда 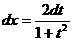 ,
, 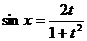 ,
, 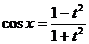 .
.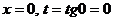 ;
; 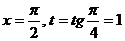 .
. .
.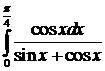 .
. и сделаем замену
и сделаем замену 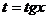 . Тогда
. Тогда 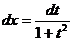 . Определим новые пределы интегрирования:
. Определим новые пределы интегрирования: 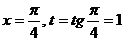 .
.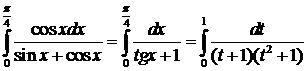 .
.
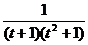 является правильной рациональной дробью, и может быть представлено как сумма простейших рациональных дробей в виде:
является правильной рациональной дробью, и может быть представлено как сумма простейших рациональных дробей в виде: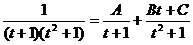 .
.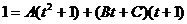 .
.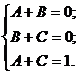
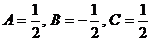 .
.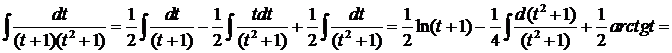
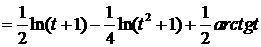 .
.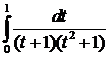 =
= 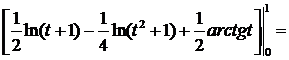
 .
.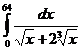 .
. ,
,  . Тогда
. Тогда 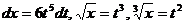 . Определим пределы интегрирования:
. Определим пределы интегрирования: 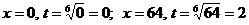 .
.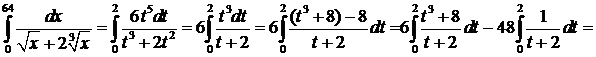
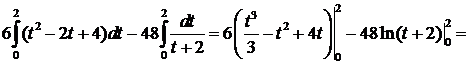
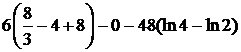 =
= 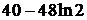 .
.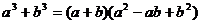 , в данном примере
, в данном примере  ; 2) свойством логарифма
; 2) свойством логарифма 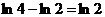 ).
).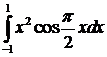 .
.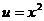 ,
, 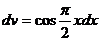 , тогда
, тогда 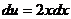 ,
, 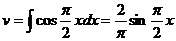 .
.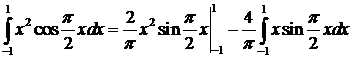 .
.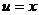 ,
, 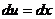 ;
; 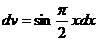 ,
, 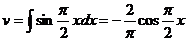 .
.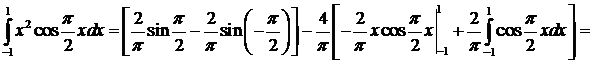
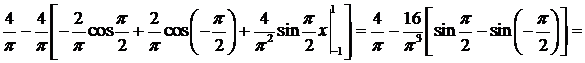
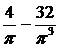 .
. .
.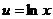 ,
, 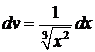 , тогда
, тогда 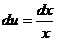 ,
, 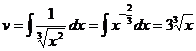 .
.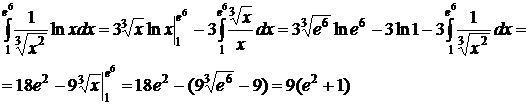
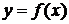 определена и непрерывна при всех
определена и непрерывна при всех 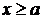 . Тогда для любого числа
. Тогда для любого числа 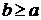 существует определенный интеграл вида
существует определенный интеграл вида  . Ранее мы имели дело с определенными интегралами, в которых пределы интегрирования были конечными числами. Теперь попытаемся расширить наши возможности в том плане, что пределы интегрирования могут быть бесконечными.
. Ранее мы имели дело с определенными интегралами, в которых пределы интегрирования были конечными числами. Теперь попытаемся расширить наши возможности в том плане, что пределы интегрирования могут быть бесконечными.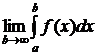 . Этот предел может быть конечным числом, может быть бесконечным, может вообще не существовать. Так вот если
. Этот предел может быть конечным числом, может быть бесконечным, может вообще не существовать. Так вот если  называется сходящимся и равным этому пределу, а если
называется сходящимся и равным этому пределу, а если 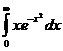 .
.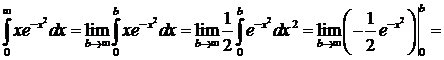
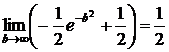 .
. .
.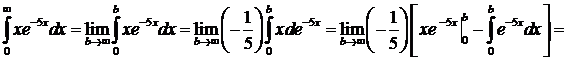
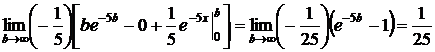 .
.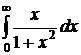 .
.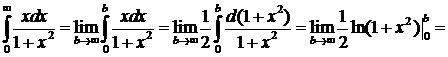
 .
.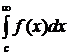 для любых
для любых 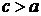 .
. . Пусть при этом
. Пусть при этом  при всех
при всех 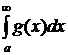 тоже сходится, при этом
тоже сходится, при этом 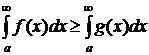 .
.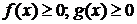 при
при 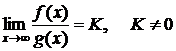 . Тогда либо оба интеграла
. Тогда либо оба интеграла