Институт прикладного психоанализа

ИЛЛЮСТРАТИВНЫЙ МАТЕРИАЛ К ДОКЛАДУ

ПО ВЫПУСКНОЙ КВАЛИФИКАЦИОННОЙ РАБОТЕ

На тему:____________________________________________________________________

___________________________________________________________________________

                                                                                                                НАУЧНЫЙ РУКОВОДИТЕЛЬ

______________________________

                                                                                                                          (должность, ученая степень,

______________________________

                                                                                                                                 ученое звание, Ф.И.О.)

                                                                              СТУДЕНТ

                                                                                                                                      _____________________________                                                                                                                                                                         

                                                                                                                                              Ф.И.О.

                                                                                                                        _____________________________

                                                                                                                                               группа

Санкт-Петербург

2018 г.

                                                      Приложение 8                                                                                    

Рис. 1. Динамика изменения интегрального показателя умственной работоспособности у операторов 1-3 групп

Таблица 1

                         Структура психических расстройств в Петербурге (в %)

Таблица 24.

Психофизиологические показатели у больных группы 4 (М+m).

Примечание. * - различия достоверны , p<0,05.

Приложение 9

«Методы математической обработки в психологии»

1. Измерительные шкалы

     Измерение – это приписывание чисел объектам и их свойствам в соответствии с определенными правилами.

     Шкала наименований предусматривает группировку предметов по классам на основании наличия у них общего признака или свойства. Классам дается наименование и присваивается значение.

     Шкала порядка (порядковое измерение) – измерение, позволяющее обнаружить в предметах различие степеней признака или свойства (ранжирование).

     Шкала интервалов (интервальное измерение) – это присвоение объектам чисе6л, при котором равные разности чисел соответствуют равным разностям значений измеряемого признака или свойства объектов.

     Особенность: произвольность выбора нулевой точки на шкале, которая вовсе не указывает на полное отсутствие признака (шкала летоисчисления, температурная шкала).

     Измерение отношений – измерение, при котором нулевая точка не произвольна, а указывает на полное отсутствие данного свойства (шкала роста, веса).

     Важным свойством шкал является их иерархичность. Шкалы более высокого уровня включают в себя свойства шкал более низкого уровня. Все математические операции, выполняемые для шкал более низкого уровня допустимы и для шкал более высокого уровня.

     Числа, представляющие собой результаты измерений в статистике называют вариантами и обозначают Хi.

Все замеры, расположенные в один ряд в порядке возрастания или убывания, образуют вариационный ряд.

Количество повторяющихся замеров в составе вариационного ряда называется частотой.

Частотное распределение ответов на вопросы анкеты.

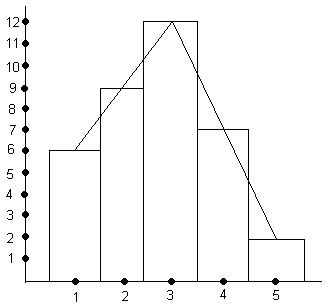
Вариационный ряд: 111 111 222222222 333333333333 4444444 55

Информацию, содержащуюся в таблице частотного распределения можно представить в виде кривой распределения.

Кривая полигона частот и гистограмма.

График, на котором связь частоты и вариант изображена столбцами и при этом соблюдены необходимые пропорции, называется гистограммой частот.

Среднее арифметическое (среднее значение, выборочное среднее)

      Х1+Х2+Х3…..Хi+Хn

Xср = —————————

                     N

Хср – среднее арифметическое,

Хi – значения вариант,

N – количество членов вариационного ряда.

       1 N

Хср = — å Xi

       N I=1

          Х1 К1+Х2 К2+Х3+К3

Xср = ———————————

                   К1+К2+К3

Кn – частота вариант.

Если измерение выполнено на шкале порядка, то среднее арифметическое вычислять нельзя. В этом случае находят медиану.

Медиана – это результат, который делит вариационный ряд пополам, причем одна половина значений лежит справа от неё, другая – слева.

Место медианы определяется по формуле:

                          N+1

место медианы = —— , где N – число членов ряда.

                           2

Медиана – это средний член вариационного ряда.

Если данные содержат нечетное число значений, например: 12,9,7,6,2, то медиана есть среднее значение для случая, когда они упорядочены, то есть медиана равна 7.

Если данные содержат четное число значений, например: 5,7,11,12, то медиана есть точка, лежащая посредине между двумя центральными значениями, когда они упорядочены.

Медиана не обладает недостатками среднего арифметического ( не выводит из масштаба измерения и не чувствительна к отскакивающим значениям)

Интересна при использовании порядковых шкал.

Например, группе из 5 испытуемых предложили оценить значимость некоторых ценностей.

При проведении номинальных измерений находят моду.

Мода – это такое значение вариационного ряда, которое встречается наиболее часто. Это варианта, частота которой максимальна.

Например: 11, 222, 333333, 444. Мода: 3.

В случае, когда все значения встречаются наиболее часто, принято считать, что вариационный ряд не имеет моды.

11, 22, 33, 44

Вариационный ряд может быть бимодальным, если два несмежных значения имеют равные значения частоты и они больше частоты других значений. Например: 11, 222, 33333, 444, 55555, 6.

Модами будут 3 и 5.

Мода используется при оценке распределении. В бимодальном ряде и может быть нормального распределения.

В нашем примере мода может быть использована для оценки единодушия.

В данном случае наиболее однозначно оценивается значимость денег, мода – 4, примерно одинакова по частоте других ценностей.

Размах выборки – разность между max и min значениями показателя.

Хmin<Хср, Хmed<Xmax

Самый грубый показатель разброса.

На примере Равенна: 35,35, 41,44,53,53,53,53,60

Размах выборки 60-34=26 условных значений.

Для измерения вариации оценок внутри выборки пользуются другими характеристиками вариационного ряда – дисперсией и средним квадратическим отклонением (стандартным отклонением). Вычисление этих значений позволяет сравнивать между собой результаты, полученные на разных выборках.

Вычисление дисперсии

Дисперсия определяется как средний квадрат отклонения варианты от ее среднего арифметического и обозначается G² или S².

Она определяется по формуле:

          1    N            2    Σ(Хi-Xср)

G² = ———— Σ (Xi-Xср) = ——————, где

       (N-1) i=1                           N-1

Хср – среднее арифметическое значение вариационного ряда,

Xi – значение каждой отдельной варианты,

N – количество вариант в вариационном ряду,

Отклонение показателя от среднего возводится в квадрат, чтобы избавиться от знака и избежать нулевых значений, т.к. он отклоняется как влево, так и вправо.

Большая дисперсия. G² = 1114.28

Малая дисперсия.

Среднее арифметическое плохо отражает среднюю тенденцию.

Измерение поляризовано. Выборка не однородна.

Если размах более 3 G, то есть отскакивающие значения.

        G

ν = ———— ×100%

          Xср

5-10% - малый разброс

Если ν (вариация) более 100, процентов, то разброс очень большой и данные использовать нельзя.

Квадратный корень из дисперсии определяется как среднее квадратическое отклонение (стандартное отклонение и обозначается буквой G сигма)

      2

G=√ G

Данная мера широко применяется при сравнении разбросов в различных группах.

Частотное распределение данных с одним и тем же средним значением, но разным разбросом.

1- большой разброс данных,

2- малый разброс данных.

Распределение, характеризующееся большими индивидуальными различиями, имеет большой разброс данных.

2. Статистическая проверка научной гипотезы.

Для определения статистической значимости полученных результатов могут использоваться различные критерии.

Параметрические критерии – включают в формулу расчета параметры распределения, то есть средние и дисперсии (t - критерий Стьюдента, критерий F и другие)

Непараметрические критерии – не включают в формулу расчета параметров распределения и основанные на оперировании частотами или рангами (критерий Q Розенбаума, критерий T Вилкоксона и другие).

t критерий Стьюдента

Используется для оценки статистической достоверности разницы между средними показателями. (Х1ср-Х2ср).

t = _Х1ср-Х2ср__ ,

         2 2

  √m1-m2

где Х1ср и Х2ср – средние арефметические

m1 и m2 – величины средних ошибок.

    G

m = —— - ошибка среднего

   √N

     G 1.63

m1 = — = ——— = 0.62

    √n  √7

     G 1.41

m2 = — = ——— = 0.53

    √n  √7

   Х1ср – Х2ср               7-4                3       3

t = ——————— = ——————— = ——— = —— = 3.69

          2    2                   2       2   √0.66 0.81

   √ m1 + m2         √ 0.62 + 0.53

Далее по специальным таблицам определяется уровень достоверности (значимости).

Пятипроцентный Р = 0.05

Однопроцентный Р = 0.01

Однопромильный Р = 0.001

Для того, чтобы найти величину уровня значимости, нужно сначала определить число степеней свободы, которые определяются по формуле:

ν = N1 + N2 – 2 , где ν – число степеней свободы.

N1 и N2 – число замеров в первом и втором рядах.

ν = 7+7-2= 12

При 12 степенях свободы tкрит. при р≥0.01=3.055

3.055<3.69. Это значит, что данная закономерность имеет место при уровне значимости 0.01.

Статистически значимые различия:

р≤0.05; р≤0.01; р≤0.001

Незначимые различия обозначаются:

р≥0.05; р≥0.01; р≥0.001

[1] Приложение является необязательным элементом и может вводиться автором в случае необходимости.

[2] Как правило, цель ставиться одна, в исключительных случаях допускается постановка 2-3 целей. Все решаемые вопросы, которые находятся в рамках основной цели, являются задачами работы.

[3] Сроки прохождения отдельных этапов выполнения ВКР, указанные в данном разделе, могут уточняться в соответствии с графиком прохождения итоговой аттестации выпускников, формируемым деканатом.