
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Как математически моделируется скорость роста усталостных трещин?Для случая циклического нагружения (усталости) скорость роста трещины может быть представлена в виде dl/dN, т.е. как изменение длины трещины за соответствующее число циклов нагружения. Представление поцикловой скорости dl/dN (равной приращению длины трещины за один цикл) условно, т.к. реально на разных стадиях трещина может прирастать не за один цикл, а за несколько циклов. Скорость приращения усталостной трещины зависит главным образом от размаха циклического изменения коэффициента интенсивности напряжений ∆К=Кmax- Kmin=Кmax(1-r) Где r= Kmin/ Кmax-коэффициент асимметрии цикла. Величина ∆К аналогична величине Если исследуется та же задача, но вместо постоянной нагрузки действует циклическая, то следует использовать выражение. Увеличение длины трещины 2l приводит к соответствующему увеличению ∆К, поскольку рост трещины происходит в процессе циклического нагружения при постоянной величине ∆σ. По достижении величиной ∆К величины вязкости разрушения Кlc(1-r), характерной для данного материала, длина трещины подрастает к критической, и происходит хрупкий долом. В первом приближении критическую длину трещины можно определить из статического критерия разрушения Кlc(1-r). Однако в процессе циклического нагружения материал портится, величина Кlc снижается, и поэтому вводят циклическую вязкость разрушения Кfc, которая меньше статической Кlc.  Назовите основные области диаграммы усталостного роста трещины. На диаграмме скорости роста усталостной трещины Где n- угол наклона кривой В области III уровень К настолько близок к Кlc, что в течение каждого цикла происходит приращение длины трещины и по прошествии некоторого времени достигается величина Кlc (или Кfc) и происходит окончательный долом образца. Эта последняя область имеет малое практическое значение для анализа срока службы при усталостном характере нагружения. Заметим, что более удобная формула Где
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 393. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
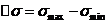 , которая обычно используется при анализе усталости образцов без трещины. Выражение для коэффициента К выбирают применительно к конкретной геометрии образца или детали и способа нагружения. Для расчета ∆К надо коэффициент К заменить на ∆К, а вместо
, которая обычно используется при анализе усталости образцов без трещины. Выражение для коэффициента К выбирают применительно к конкретной геометрии образца или детали и способа нагружения. Для расчета ∆К надо коэффициент К заменить на ∆К, а вместо 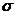 подставить величину размаха напряжений ∆
подставить величину размаха напряжений ∆ 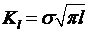
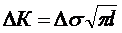
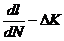 можно выделить три характерные области. Область I малого размаха ∆К, в которой имеющиеся в образце трещины растут медленно. Уровень ∆К, ниже которого трещина не растет, называют пороговым ∆Кth. Далее следует область I I, в которой соблюдается линейное соотношение между lg
можно выделить три характерные области. Область I малого размаха ∆К, в которой имеющиеся в образце трещины растут медленно. Уровень ∆К, ниже которого трещина не растет, называют пороговым ∆Кth. Далее следует область I I, в которой соблюдается линейное соотношение между lg 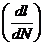 и lg(∆К) в широком диапазоне размаха ∆К. Это соотношение справедливо для большинства конструкционных материалов( формула Париса)
и lg(∆К) в широком диапазоне размаха ∆К. Это соотношение справедливо для большинства конструкционных материалов( формула Париса)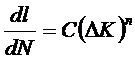
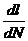 как функции
как функции 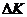 , в логарифмических координатах, 2≤n≤8 (большие величины n отвечают более хрупкому состоянию материала); С- эмпирическая константа для участка кривой, где справедливо линейное соотношение. Размерность этой константы-
, в логарифмических координатах, 2≤n≤8 (большие величины n отвечают более хрупкому состоянию материала); С- эмпирическая константа для участка кривой, где справедливо линейное соотношение. Размерность этой константы- 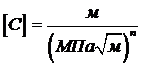
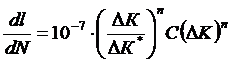 (м/цикл),
(м/цикл),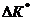 =
= 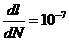 м/цикл
м/цикл