
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Связь отображений с разбиением множества на классы ⇐ ПредыдущаяСтр 4 из 4 Рассматриваемое понятие отображения тесно связано с понятием разбиения множества на классы (см. п. 3.3. раздела 3). Пусть F — отображение множества X в множество Y. Собрав в один класс все элементы из X, образы которых в Y совпадают, мы получим, очевидно, некоторое разбиение множества X. Обратно, рассмотрим произвольное множество X и некоторое его разбиение на классы. Пусть Y — совокупность тех классов, на которые разбито множество X. Ставя в соответствие каждому элементу x
Примеры 6.1.8.
1) Спроектируем плоскость XOY на ось х. Прообразы точек оси х — вертикальные прямые. Следовательно, этому отображению отвечает разбиение плоскости на параллельные прямые.
2)Разобьем все точки трехмерного пространства на классы, объединив в один класс точки, равноудаленные от начала координат. Каждый класс представляет собой сферу некоторого радиуса. Совокупность всех этих классов можно отождествить с множеством всех точек, лежащих на луче [0, +∞). Итак, разбиению трехмерного пространства на концентрические сферы отвечает отображение этого пространства на полупрямую.
3) Объединим в один класс все действительные числа с одинаковой дробной частью. Этому разбиению отвечает отображение прямой линии на окружность единичной длины (это отображение можно представить как результат наматывания нити (числовой прямой) на катушку с единичной длиной окружности катушки. Тогда каждой точке (дробной части) на катушке будет соответствовать множество точек на «намотанной» на катушку прямой). Вопросы для самоконтроля: 1. Дайте определение отображения 2. Приведите свои примеры отображений, заданных на числовых и нечисловых множествах 3. Дайте определение функции, последовательности, тождественного и постоянного отображений 4. Приведите пример отображения, для выбранного отображения укажите образы и прообразы выбранных точек и множеств. 5. Являются ли биективными отображения y = sin x, y = x+2, y = x4 ? 6. Сформулируйте и докажите признак обратимости отображений 7. Сформулируйте основные свойства отображений. Приведите примеры 8. Как связаны отображения и разбиение множества на классы?
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 331. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
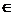 X тот класс (т.е. элемент из Y), к которому x принадлежит, мы получим отображение множества X на множество Y.
X тот класс (т.е. элемент из Y), к которому x принадлежит, мы получим отображение множества X на множество Y.