
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Понятие отображения. Примеры (частные случаи) отображенийСтр 1 из 4Следующая ⇒ Раздел 6. Введение в математический анализ.
Тема 6.1. Отображения
6.1.1.Понятие отображения. Примеры (частные случаи) отображений 6.1.2.Сложное отображение. Сужение отображения 6.1.3. Образ и прообраз точки и множества при отображении. 6.1.4. Обратимое отображение. Обратное отображение 6.1.5.Сюръективное и инъективное отображения. Биекция 6.1.6.Критерий обратимости отображений 6.1.7.Основные свойства отображений 6.1.8. Связь отображений с разбиением множества на классы
Программные положения Понятие отображения является одним из ключевых в математическом анализе. С другой стороны без понятия отображения в психологии невозможно, например, создание корректно работающих тестов.
Методические рекомендации Внимательно ознакомьтесь с текстом лекции. Приведите свои примеры разных видов отображений. Обратите внимание, что отображение– это не один объект, а три, причем для равенства отображений необходимо совпадение всех трех. Примите к сведению, что функция – один из видов отображений, но не единственный, соответственно, понятие отображения является более общим.
Рекомендуемая литература
Контрольные вопросы 1. Дайте определение отображения 2. Приведите свои примеры отображений, заданных на числовых и нечисловых множествах 3. Дайте определение функции, последовательности, тождественного и постоянного отображений 4. Приведите пример отображения, для выбранного отображения укажите образы и прообразы выбранных точек и множеств. 5. Являются ли биективными отображения y = sin x, y = x+2, y = x4 ? 6. Сформулируйте и докажите признак обратимости отображений  7. Сформулируйте основные свойства отображений. Приведите примеры 8. Как связаны отображения и разбиение множества на классы?
Понятие отображения. Примеры (частные случаи) отображений Наряду с понятиями множества и элемента в математике первичным понятием является понятие соответствия. Это понятие неявным образом присутствует и в понятии множества, поскольку понятие множества предполагает, что каждый элемент данного множества обладает определенным свойством, отличающим его от элементов, не входящих в это множество. Иначе говоря, каждому из рассматриваемых элементов поставлено в соответствие некоторое свойство, позволяющее судить о том, является этот элемент элементом данного множества или нет. Среди всевозможных соответствий важную роль в математике играют соответствия, называемые отображениями. Опишем эти соответствия. Определение 6.1.1. Отображение F множества X в множество Y - это правило, которое каждому элементу x , принадлежащему множеству X , сопоставляет некоторый, но единственный для данного х , элемент y из множества Y. x называется аргументом отображения (независимой переменной), а F(x)=y – его значением (соответственно, зависимой переменной. Множества X и Y необязательно являются числовыми.
Обозначения: F : X→Y («F действует из множества X в множество Y») y = F(x) x {F(x)} Синонимами отображения являются «правило, сопоставляющее…», «оператор», «морфизм», «семейство», «оператор», «функционал», «функция» (используется в частных случаях). Иногда, как например в классическом учебнике А.Н.Колмогорова и С.В.Фомина «Элементы теории функций и функционального анализа», термин «функция» используется в широком смысле вместо или параллельно с термином «отображение» . В этом случае отображения обозначаются, как традиция предписывает для функций, строчными латинскими буквами: f : X→Y («f действует из множества X в множество Y») y = f(x).
Примеры 6.1.1.
1) Х = { множество студентов 1 курса ВЕИП отделения дистанционного обучения} Y = {2, 3, 4, 5} F(x) – экзамен по курсу «Высшая математика» 2) X={1, 2, …n } Y={ множество студентов 1 курса ВЕИП отделения дистанционного обучения } F(x) – нумерованный список студентов, расположенных, например, по алфавиту 3) X = { множество студентов 1 курса ВЕИП отделения дистанционного обучения } Y = {множество преподавателей ВЕИП} F(x) – научный руководитель 4) X = Y = (- ∞, ∞), F(x) = 5x + 4 5) X и Y – множества непрерывных функций, F – оператор дифференцирования
Замечания 6.1.1. 1) Задать отображение - значит задать 3 объекта: X – множество задания отображения, Y – множество его значений и F – собственно правило. То есть, задать (X,Y,F). 2) Если у нас имеется другое отображение , то есть другая тройка (X’, Y’ F’), то совпадать они будут только в случае равенства всех трех элементов троек: X = X’ они заданы на одном множестве Y = Y’ они действуют в одно и то же множество F = F’ действуют одинаково, то есть Например, пусть 1.X = Y = (- ∞, + ∞) F(x) = |x| 2.X’ = Y’ = (- ∞, + ∞) F’(x) = эти два отображения совпадают 3. Отображение F’’(x) = 3) Отображение F можно определить и как бинарное отношение (то есть множество упорядоченных пар (x, y)
Частными случаями отображений являются:
1. Функции Функция – это отображение (X,Y,F), где множество Y – числовое, то есть
2. Последовательности Последовательность – это отображение (X,Y,F), где множество Х – множество натуральных чисел. Чтобы задать такую последовательность, достаточно задать таблицу
Такая таблица однозначно определяет отображение, задающее совокупность {F(1),F(2),F(3),…, F(n),… }, она же { F1 , F2, F3, …, Fn, …}. Если же множество Y является числовым, последовательность называется числовой и может рассматриваться как частный случай функции. Примером может служить, скажем, арифметическая прогрессия, каждый элемент которой выражается через его порядковый номер n: an = a1 + (n – 1)d Вообще, любую последовательность чисел a1, a2, a3, . . . можно рассматривать как множество значений некоторой функции y = F(n), причем областью изменения независимого переменного при этом является множество натуральных чисел. Только ради сокращения записи принято обозначать n-й член последовательности символом an, вместо того чтобы употреблять более отчетливое функциональное обозначение F(n). Выражения S1(n) = 1 + 2 + . . . + n = n(n + 1) S2(n) = 12 + 22 + . . . + n2 = n(n + 1)(2n + 1) S3(n) = 13 + 23 + . . . + n3 = n2(n + 1)2 являются функциями целого переменного n.
3. Конечные упорядоченные наборы Конечный упорядоченный набор – отображение, в котором в роли множества X выступает отрезок натурального ряда. X = {1, 2, 3, …, m} Соответствующая ему таблица имеет вид:
Если m = 2 X = {1, 2} и (F1 , F2) – упорядоченная пара, m = 3 X = {1, 2, 3} и (F1 , F2, F3) – упорядоченная тройка, И т.д Не стоит путать эти наборы с конечными множествами, поскольку они, в отличие от множеств, являются упорядоченными
4. Тождественные отображения Тождественное (идентичное) отображение – это (X, Y, F), где X=Y и F(x) = x, Обозначение: отображение F = idX – тождественное на X, idX (x) = x , x
5. Постоянные отображения Постоянное отображение – это отображение, ставящее любому аргументу в соответствие одно и то же значение F: X Y
6. Семейство Семейство – совокупность {F(x)}
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 446. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
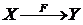
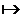 F(x)
F(x)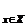 , X- множество индексов, x – значок, индекс
, X- множество индексов, x – значок, индекс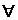 x
x 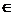 X F(x) = F’(x)
X F(x) = F’(x)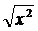
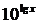 с ними не совпадает, поскольку X’’ = (0, + ∞)
с ними не совпадает, поскольку X’’ = (0, + ∞)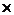 Y), которое удовлетворяет следующему условию: для любого x
Y), которое удовлетворяет следующему условию: для любого x 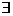 y0
y0