
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Сложное отображение. Сужение отображенияОпределение 6.1.2. (1) Пусть F: X → Y G: Y → Z, то есть отображение G определено на области значений Y отображения F Тогда отображение H: X →Z по правилу H(x) = G(F(x)) = G[F(x)] называется сложным отображением или суперпозицией (композицией) отображений F и G (обратите внимание: именно в таком порядке!) и обозначается H (x)= (G ◦ F)(x)
Операцию композиции иногда приходится проводить несколько раз подряд. Заметим, что эта операция ассоциативна, то есть, H ◦(G◦ F) = (H ◦G) ◦F
H ◦ G ◦F (x) = H((G ◦ F)(x) = H(G(F(x))) = (H ◦ G)(F(x)) = ((H ◦G)◦ F)(x)
Пример 6.1.2 (1). Пусть X={1,2,…,n} Y={студенты 1 курса ВЕИП отделение дистанционного обучения} Z = {темы курсовых работ студентов 1 курса} F(x) – каждому номеру ставится в соответствие фамилия студента, например по алфавитному принципу, т.е. формируется список G(y) – каждому студенту ставится в соответствие тема курсовой работы Тогда композиция отображений H (x)= (G ◦ F)(x) – нумерованный список тем курсовых работ Определение 6.1.2 (2) Пусть отображение F: X →Y, Отображение Примеры 6.1.2 (2). 1) Пусть X={1,2,…,n} Y={студенты 1 курса ВЕИП отделение дистанционного обучения} F(x) – нумерованный алфавитный список студентов.
2) X = Y=(-∞, +∞), F(x) = x2 .
Образ и прообраз точки и множества при отображении. Определения 6.1.3. 1)Если а — элемент из X, то отвечающий ему элемент b = F(a) из Y называется образом точки а (при отображении F). 2)Совокупность всех тех элементов а из X, образом которых является данный элемент b  3)Пусть А — некоторое множество из X, совокупность {F(а): а 4) В свою очередь для каждого множества В из Y определяется его полный прообраз F-1(B), а именно: F-1(B)есть совокупность всех тех элементов из X, образы которых принадлежат В. (см.рис.6.1.3.)
Может оказаться, что ни один элемент b из В не имеет непустого прообраза, тогда и прообраз F-1(B)будет пустым множеством. Примеры 6.1.3. 1)Пусть X = Y = (- ∞ , + ∞), F(x) = x3 . a = 2 b=64 A= [2,4], B = F(A) = [8, 64] – образ множества А при отображении F
Обратимое отображение. Обратное отображение Определение 6.1.4. Отображение F называется обратимым, если существует отображение G такое, что: Такое отображение G называется обратным (к) отображению F и обозначается G = F-1 (обратите внимание: (-1) – не показатель степени, а специальное обозначение для обратного отображения).
Замечания 6.1.4. 1) G – обратное к F , это означает, что G ◦ F = idX , F ◦ G = idY 2) F-1 (B) – прообраз множества B при отображении F, в то же время F-1 (B) – образ множества B при обратном отображении F-1 . Формально они разные, но всегда совпадают.
Сюръективное и инъективное отображения. Биекция Определения 6.1.5. 1) Сюръекция Отображение 2)Инъекция Отображение 3) Биекция (биективное отображение, взаимно однозначное соответствие) Отображение называется биекцией, если оно является одновременно и инъекцией, и сюръекцией . То есть, F переводит разные элементы множества X в различные элементы множества Y, кроме того, полным образом множества X является множествоY . Функция
Примеры 6.1.5. 1)Англо-русский словарь устанавливает соответствие между множеством английских и русских слов. Это соответствие не является функциональным (так как одному английскому слову, как правило, ставится в соответствие несколько русских слов); кроме того, оно практически никогда не является полностью определенным: всегда можно найти английское слово, не содержащееся в данном словаре. 2) Позиция на шахматной доске представляет собой взаимно однозначное соответствие между множеством оставшихся на доске фигур и множеством занятых ими полей. 3)Различные виды кодирования — кодирование букв азбукой Морзе, представления чисел в различных системах счисления, секретные шифры, входящие и исходящие номера в деловой переписке и др. — являются соответствиями между кодируемыми объектами и присваиваемыми им кодами. Эти соответствия, как правило, обладают всеми свойствами взаимно однозначного соответствия, кроме, быть может, одного — сюръективности. Единственность образа и прообраза в кодировании гарантирует однозначность шифровки и дешифровки. Отсутствие сюръективности означает, что не всякий код имеет смысл, т. е. соответствует какому- либо объекту. Например, кодирование телефонов г. Санкт-Петербурга семизначными номерами не сюръективно, так как некоторые семизначные номера не соответствуют никаким телефонам. |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 438. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 .
.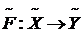 называется сужением отображения F , если
называется сужением отображения F , если  выполняется
выполняется  . Обозначение
. Обозначение  .
.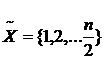 ([n/2], если n – нечетное)
([n/2], если n – нечетное) - список первой половины курса
- список первой половины курса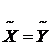 = [0, +∞),
= [0, +∞), 
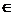 Y, называется прообразом (или, точнее, полным прообразом) элемента b и обозначается F-1(b).
Y, называется прообразом (или, точнее, полным прообразом) элемента b и обозначается F-1(b). Рис. 6.1.3.
Рис. 6.1.3. G(F(x)) = x
G(F(x)) = x F(G(y)) = y
F(G(y)) = y называется сюръективным (или сюръекцией, или отображением на
называется сюръективным (или сюръекцией, или отображением на  ), если каждый элемент множества
), если каждый элемент множества  , то есть
, то есть  . Для случая числовых функций это выражается как «функция, принимающая все возможные значения».
. Для случая числовых функций это выражается как «функция, принимающая все возможные значения». множества
множества  ) называется инъекцией (или вложением), если разные элементы множества
) называется инъекцией (или вложением), если разные элементы множества 
 называется биекцией (и обозначается
называется биекцией (и обозначается  ), если она:
), если она: .
. .
.