
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Критерий обратимости отображенийТеорема 6.1.6. Критерий обратимости отображений F: X→Y. Отображение F обратимо тогда и только тогда, когда F является биекцией. Иными словами, отображение F обратимо (т.е. Пример 6.1.6. Пусть X={1,2,…,n} Y={студенты 1 курса ВЕИП отделение дистанционного обучения} F(x) – каждому номеру ставится в соответствие фамилия студента, например по алфавитному принципу, т.е. формируется список. Для того, чтобы стало возможным обратное действие, т.е. определение номера по фамилии студента, необходимо и достаточно, чтобы: - разным номерам соответствовали разные студенты (по одному студенту на номер) - у каждого студента был свой номер Доказательство 1) F обратимо
G(F(x1)) = x1 G(F(x2)) = x2, x1 ≠ x2 (по определению обратимого отображения), т.е. в разных точках F(x1 ) и F(x2)отображение G имеет разные значения,
2) F обратимо Отображение F – биекция, то есть оно сюръективно и инъективно F – сюръективно, значит F – инъективно, поэтому такой x единственный, то есть, Тем самым определено отображение G: Y→ X Проверим, что это обратное отображение: F(G(y)) = F (xy ) = y для G(F(x)) = G(y) = x, так как G(y) – единственное решение уравнения F(x)=y (из определения отображения G), а равенство G(y) другому значению x’ приводит к противоречию:  G(y) = x’≠x Тем самым теорема доказана. Основные свойства отображений Теорема 6.1.7.(1) Прообраз суммы двух множеств равен сумме их прообразов: F-1(A U В) = F-1(A) U F-1(В) Доказательство. Пусть элемент x принадлежит множеству F-1(A U В). Это означает, что F(x) Обратно, если х из множеств F-1(A) или F-1(В), т.е. F(x) принадлежит хотя бы одному из множеств А или В, следовательно, F(x) Теорема 6.1.7.(2) Прообраз пересечения двух множеств равен пересечению их прообразов: F-1(A ∩ В)= F-1(A) ∩ F-1(В) Доказательство. Если х F(x) х Обратно, если х то F(x) х
Теорема 6.1.7.(3) Образ суммы двух множеств равен сумме их образов F(A U В) = F(A) U F(В) Доказательство. Если у Обратно, если у Теорема 6.1.7.(4) Образ пересечения двух множеств, вообще говоря, не совпадает с пересечением их образов. (Замечание: Оборот «вообще говоря» используется в математических выкладках в смысле «как правило», «обычно», «обратное нетипично».) Приведем контрпример, подтверждающий утверждение. Рассмотрим, например, отображение - проектирование плоскости на ось x. Тогда отрезки (0≤x≤1, y = О) и (0≤x≤1 , y = 1) не пересекаются, а в то же время их образы совпадают. |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 808. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 F – биективное отображение (т.е. F является сюръективным и инъективным). То есть, необходимо доказать по сути четыре утверждения
F – биективное отображение (т.е. F является сюръективным и инъективным). То есть, необходимо доказать по сути четыре утверждения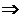 F биекция
F биекция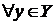 определим
определим  Тогда F(x) =F(G(y)) = y (по определению обратимого отображения). Таким образом,
Тогда F(x) =F(G(y)) = y (по определению обратимого отображения). Таким образом, 
 такой, что F(x)=y, т.е. F – сюръекция (по определению)
такой, что F(x)=y, т.е. F – сюръекция (по определению) , и является инъективным
, и является инъективным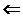 F биекция
F биекция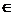 A U В, т.е. F(x)
A U В, т.е. F(x) 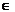 А и F(x)
А и F(x)