
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Подобие гидромеханических процессовСтр 1 из 4Следующая ⇒ Лекция 4 Моделирование технологических процессов
Для проектирования новых и оптимизации существующих аппаратов необходимо знание в них полей w, р, Т и сi. Определить эти поля можно было бы двумя способами: теоретическим и экспериментальным. Теоретический способ – решение дифференциальных уравнений, составляющих исчерпывающие описание процессов переноса. Задача труднодостижимая. Экспериментальный способ дорогой, трудоемкий и технически сложный. В связи с этим в инженерной практике получил подход, называемый моделированием. Моделирование– это изучение объекта-оригинала с помощью замещающей его модели, включающей построение модели, ее исследование и перенос полученных результатов на объект - оригинал. Объект-оригинал – объект, свойство которого подлежат изучению методом моделирования. Модель – объект, отражающий свойства оригинала и заменяющий его при проведении исследований. Наибольшее распространение в инженерной практике получила математическое и физическое проектирование.
Математическое моделирование
Математическое моделирование – исследование процессов или явлений на основе математических моделей. Математической моделью процессов является исчерпывающее математическое описание процессов переноса. Но эти модели сложные, уравнения, в основном, не решаются. Поэтому их упрощают, путем оценки значимости членов. Если этот способ невозможен (члены уравнения одного порядка), то сознательно огрубляют исчерпывающие описание процесса. Например: трехмерное описание приводит к одномерному – от входа в аппарат к выходу. При этом коэффициенты переноса заменяются на некие параметры модели. Описание этих параметров, т.е. идентификация модели, проводят путем сопоставления результатов физического и численного экспериментов.  Любая модель неполно отображает оригинал. Поэтому следующим этапом моделирования является проверка адекватности модели - соответствия ее моделируемому объекту. Это достигается путем сопоставления результатов моделирования с численным либо физическим экспериментом. Если модель в недостаточной степени соответствует оригиналу, проводят ее коррекцию. Конечным этапом математического моделирования является использование полученной модели для описания объекта, либо уже существующего, либо проектируемого. Итак, этапы математического моделирования: - составление математической модели; - идентификация модели; - проверка адекватности модели, при необходимости коррекция; - использование модели для описания объекта-оригинала. Современное материальное обеспечение математического моделирования – компьютеры, возможности которых велики. Физическое моделирование
Физическое моделирование проводится на основе экспериментального изучения материальных моделей объекта. При этом возникают три проблемы: - какую модель использовать (форма, размер, среда), - какие характеристики измерять, - как перенести результаты исследования с модели на объект. Эти проблемы решаются с помощью теории подобия, являющейся теоретической основой физического моделирования.
Теория подобия
Подобие в широком смысле – это возможность распространения результатов экспериментов с модели на оригинал. В узком смысле подобие – это тождественность описания полей соответствующих величин модели и оригинала в обобщенных переменных или, по-другому, постоянство отношения сходственных величин модели и оригинала. Далее подобие будем понимать в узком смысле. Подобные объекты описываются одной системой дифференциальных уравнений и имеют подобные условия однозначности (геометрическое подобие, временное подобие, подобие физических величин, подобие начальных и граничных условий). Геометрическое подобие – постоянство отношения всех сходственных линейных размеров модели и оригинала.
где Временное подобие (гомохранность) – постоянство отношения сходственных интервалов времени модели и оригинала:
Если Подобие физических величин – постоянство отношения физических величин для модели и оригинала в сходственных точках в сходственные моменты времени:
Подобие модели и объекта предполагают подобие полей физических величин:
Подобие начальных условий – подобие полей всех физических величин в начальный момент времени. Подобие граничных условий – постоянство отношения соответствующих величин на границах модели и оригинала. Константа подобия – отношения одноименных величин модели и оригинала. Они постоянны для различных сходственных точек подобных систем. Инварианты подобия – безразмерные отношения величин, характеризующих модель или оригинал. Инварианты подобия – еще называют обобщенными или безразмерными переменными. Симплексы подобия – инварианты подобия, представляющие собой отношения однородных величин:
Критерии подобия – инварианты подобия, представляющие собой отношения разнородных, сложных величин: Например
Определяющие критерии подобия составлены из величин, входящих в условия однозначности. Определяемые критерии подобия содержат величины, которые необходимо определить. Наиболее простой метод получения критериев подобия заключается в следующем: дифференциальные уравнения приводятся к безразмерному виду делением всех членов на один из них. Полученные комплексы являются критериями подобия. Теоремы подобия: 1. Подобные объекты характеризуются численно равными критериями подобия. 2. Решение дифференциального уравнения (уравнений) описывающего объект, может быть представлено в виде зависимости между критериями подобия. 3. Объекты подобны, если они описываются одной системой дифференциальных уравнений, имеют подобные условия однозначности и их определяющие критерии равны. Математическая зависимость между критериями и симплексами подобия, характеризующая данный процесс переноса субстанции, называется критериальным уравнением:
φ
Если определяемый критерий
Обычно критериальные уравнения имеют вид степенной зависимости:
Величины А, а1, а2, …, в1, в2 … - определятся экспериментально. Если какой-либо из определяющих критериев слабо влияет на определяемый критерий, то его исключают из уравнения.
Подобие гидромеханических процессов
Запишем для вертикальной оси z уравнения Навье – Стокса:
Уравнение (2.96) преобразуем следующим образом: отбросив знаки математических операторов, делим одну часть уравнения на другую и находим критерии подобия.
ρg, (III)
Члены в правой части уравнения разделим на
где Fr – критерий Фруда. Этот критерий отражает влияние сил тяжести на движение жидкости, является мерой отношения сил инерции и тяжести.
где Eu– критерий Эйлера. Критерий Эйлера является мерой отношения сил поверхностного давления и инерции.
где Re – критерий Рейнольдса. Критерий Рейнольдса является мерой отношения сил инерции и вязкого трения. Внутри левой части уравнения имеем:
где Но – критерий гомохронности (для неустановившегося движения). Все критерии, симплексы, константы подобия безразмерные величины. Для гидродинамического подобия двух явлений требуется:
Гi =idem (i=1,2,3…n),
Re = idem, Eu = idem, Fr = idem, Ho = idem. (2.101)
Решение уравнения Навье – Стокса может быть представлено критериальным уравнением вида:
f(Re, Ho, Eu,Fr)=0. (2.102)
В ряде случаев (течение жидкости по трубе, например) последнее уравнение должно быть дополнено симплексами подобия:
f(Re, Ho, Eu, Fr, Гi)=0. (2.103)
Обычно определяют Δp, тогда
Eu= f(Re, Ho, Fr, Гi). (2.104)
Для установившихся процессов критерий гомохронности Ho = 0 и должен быть исключен из уравнений, а критерием Fr можно пренебречь вследствие того, что сила тяжести мала по сравнению с силами инерции и вязкого трения. Таким образом, зависимость (2.104) сводится к виду:
Eu = f(Re, Гi). (2.105)
При развитых турбулентных режимах, в зоне автомодельности сопротивления трения по критерию Re, зависимость еще более упрощается и принимает вид:
Eu= f(Гi). (2.106)
Результаты экспериментальных данных обрабатываются, обычно, в виде степенной зависимости:
Константы A, ai определяются экспериментально.
Рассмотрим подобие граничных условий. Вязкий поток импульса через границу раздела фаз
Тот же поток можно выразить в виде линейной зависимости от разности wx на границе и в ядре потока среды:
где γ – коэффициент импульсоотдачи. Тогда получим:
Проведя формальное преобразование получим:
где l – характерная линейная величина, Гидродинамический критерий Нуссельта является безразмерной формой коэффициента импульсоотдачи. Поскольку поле скорости wx однозначно определяет коэффициент γ, решение уравнений Навье – Стокса можно представить следующим образом:
Для многих практически важных случаев число определяющих критериев может быть сокращенно. Влияние силы тяжести на wx зачастую можно пренебречь и исключить критерий Фруда. Для стационарных процессов исключается критерий гомохронности. Процесс импульсоотдачи может стать автомодельным и по отношению к критерию Рейнольдса.
Подобие тепловых процессов Для полного описания конвективного переноса теплоты необходимо присоединить к уравнению Фурье-Кирхгофа уравнение Навье-Стокса и неразрывности, а также алгебраическое уравнение зависимости вязкости от температуры. Однако, это трудно разрешимая задача. Поэтому рассмотрим подобие. Критерии подобия тепловых процессов выводятся из уравнения Фурье-Кирхгофа:
Преобразуем уравнение Фурье-Кирхгофа формальным, но простым способом, отбрасывая знаки математических операторов:
Далее, разделив одну часть уравнения на другую, находим критерии подобия.
Критерий Фурье
Критерий Пекле Pe характеризует отношение между интенсивностью переноса теплоты конвекцией и теплопроводностью в движущемся потоке. Рассмотрим подобие граничных условий. Тепловой поток на границе раздела фаз можно выразить с помощью уравнения Фурье:
Тот же поток можно выразить в виде линейной зависимости от разности температур на границе и в ядре потока жидкости
где α – коэффициент теплоотдачи. Тогда получим:
Проведя формальное преобразование (2.118) имеем:
Критерий Нуссельта Nu характеризует отношение суммарного переноса теплоты конвекцией и теплопроводностью (т.е. теплоотдачей) к теплоте , передаваемой теплопроводностью. Для подобия процессов теплообмена необходимо Кроме того, необходимым условием подобия процессов переноса теплоты является соблюдение и гидродинамического подобия. Тогда критериальное уравнение теплоотдачи имеет вид:
или
Критерий Эйлера в уравнение не вошел, т.к. Eu=f(Re) . Преобразование критерия Пекле дает:
Критерий Прандтля Pr=ν/a – характеризует подобие физических свойств теплоносителей. Для газов Pr≈1, жидкостей Pr=10 - 100 . Для установившегося процесса теплообмена:
При вынужденной теплоотдаче критерием Fr можно пренебречь:
Обычно критериальное уравнение представляют в виде степенной зависимости:
Здесь А, а1-6 – экспериментально определяемые коэффициенты.
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 199. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , (2.88)
, (2.88)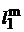 и
и  - сходственные линейные размеры модели и объекта;
- сходственные линейные размеры модели и объекта;  - константа геометрического подобия.
- константа геометрического подобия. . (2.89)
. (2.89) =1, то имеем синхронность.
=1, то имеем синхронность. . (2.90)
. (2.90) - гидродинамическое подобие (подобие полей скоростей);
- гидродинамическое подобие (подобие полей скоростей); - тепловое подобие (подобие полей температуры);
- тепловое подобие (подобие полей температуры); - концентрационное подобие (подобие полей концентраций).
- концентрационное подобие (подобие полей концентраций). . (2.91)
. (2.91) . (2.92)
. (2.92) . (2.93)
. (2.93) , то получаем:
, то получаем: . (2.94)
. (2.94) . (2.95)
. (2.95) (2.96)
(2.96)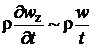 , (I)
, (I) ~
~  , (II)
, (II) , (IV)
, (IV) . (V)
. (V) :
: ,
, 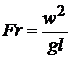 , (2.97)
, (2.97)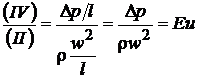 ,
,  , (2.98)
, (2.98) ,
,  , (2.99)
, (2.99)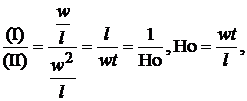 (2.100)
(2.100) . (2.107)
. (2.107) можно определить по закону Ньютона:
можно определить по закону Ньютона: . (2.108)
. (2.108) , (2.109)
, (2.109) . (2.110)
. (2.110) , (2.111)
, (2.111) - гидродинамический критерий Нуссельта.
- гидродинамический критерий Нуссельта. . (2.113)
. (2.113) (I),
(I),  , (II)
, (II)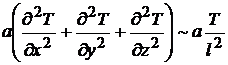 . (III)
. (III) , (IV)
, (IV)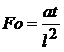 . (2.114)
. (2.114)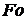 характеризует распространение теплоты теплопроводностью при изменении температуры во времени, является аналогом критерия гомохронности Ho.
характеризует распространение теплоты теплопроводностью при изменении температуры во времени, является аналогом критерия гомохронности Ho.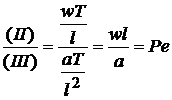 ,
, 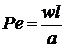 . (2.115)
. (2.115) . (2.116)
. (2.116)
 , (2.117)
, (2.117)
 . (2.118)
. (2.118) , (I)
, (I)  , (II)
, (II) ,
, 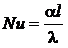 . (2.119)
. (2.119) ,
,  ,
,  .
. , (2.120)
, (2.120) . (2.121)
. (2.121) . (2.122)
. (2.122)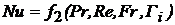 . (2.123)
. (2.123) . (2.124)
. (2.124) . (2.125)
. (2.125)