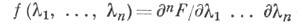Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Свойства взаимной корреляционной функции ⇐ ПредыдущаяСтр 4 из 4 1. 2.Прибавление к случайным функциям неслучайных слагаемых не меняет взаимной корреляционной функции, то есть: 3.Неслучайные множители с1 (t) и с2 (t) случайных функций X (t) и Y (t), соответственно, можно следующим образом выносить за знак взаимной корреляционной функции: 4. Доказательства всех свойств совершенно аналогичны доказательствам свойств корреляционной функции одной случайной функции. Нормированной взаимной корреляционной функцией случайных функций X (t) и Y (t) называется: Замечание. Свойства нормированной взаимной корреляционной функции отличаются от свойств исходной взаимной корреляционной функции так же, как свойства нормированной корреляционной функции одной случайной функции отличаются от ее ненормированного аналога. Теорема. Корреляционная функция суммы двух случайных функций Доказательство.По определению корреляционной и взаимной корреляционной функций, а также на основе свойства 3 математического ожидания имеем: Следствие. Корреляционная функция суммы двух некоррелированных случайных функций Пример 1.3 Найти взаимную корреляционную функцию случайных функций Спектральная плотность СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ стационарного случайного процесса или однородного случайного поля в n-мерном пространстве - преобразование Фурье ковариационной функции стационарного в широком смысле случайного процесса или однородного в широком смысле случайного поля. Стационарные случайные процессы и однородные случайные поля, преобразование Фурье ковариационной функции которых существует, наз. процессами, имеющими спектральную плотность.  Пусть есть n-мерный стационарный случайный процесс, а - его спектральное представление (Ф k - спектральная случайная мера, отвечающая k-й компоненте Xk(t) многомерного случайного процесса X(t)); интегрирование здесь проводится в пределах если все элементы спектральной меры В частности, если для процесса X(t), Где - ковариационная функция процесса X(t), то X(t) имеет спектральную плотность и Аналогично обстоит дело и в случае процессов X(t) с непрерывным временем t. Спектральная плотность и |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 198. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
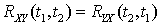 .
.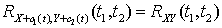 .
.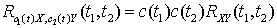 .
.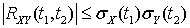 .
.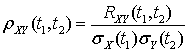 .
.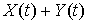 равна:
равна: 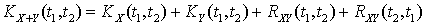 .
.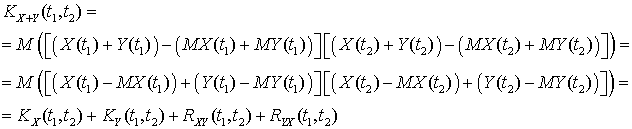 .Применяя первое свойство взаимной корреляционной функции к последнему слагаемому, можем переписать выражение в виде:
.Применяя первое свойство взаимной корреляционной функции к последнему слагаемому, можем переписать выражение в виде: 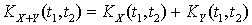 .
.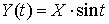 и
и 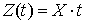 , где X — случайная величина с MX = 3 и DX = 2.Используя свойства взаимной корреляционной функции случайных функций, рассмотренные выше, имеем:
, где X — случайная величина с MX = 3 и DX = 2.Используя свойства взаимной корреляционной функции случайных функций, рассмотренные выше, имеем: 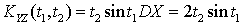 .
.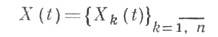
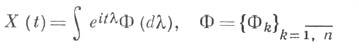
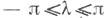 в случае дискретного времени tи в пределах
в случае дискретного времени tи в пределах 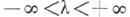 в случае непрерывного времени t. Процесс X(t) имеет спектральную плотность.
в случае непрерывного времени t. Процесс X(t) имеет спектральную плотность.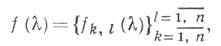
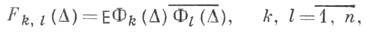
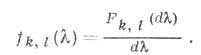 абсолютно непрерывны и
абсолютно непрерывны и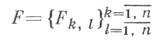
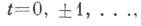 выполняется соотношение
выполняется соотношение 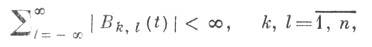
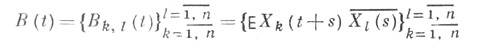
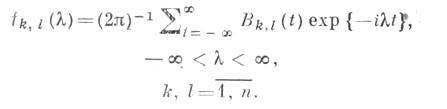
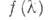 иногда наз. спектральной плотностью 2-го порядка, в отличие от старших С. п. Однородное n-мерное случайное поле X(t1, . . ., tn) имеет С. п.
иногда наз. спектральной плотностью 2-го порядка, в отличие от старших С. п. Однородное n-мерное случайное поле X(t1, . . ., tn) имеет С. п.  если его спектральная функция
если его спектральная функция 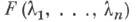 обладает тем свойством, что ее смешанная производная
обладает тем свойством, что ее смешанная производная 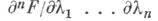 существует почти всюду, причем
существует почти всюду, причем