Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
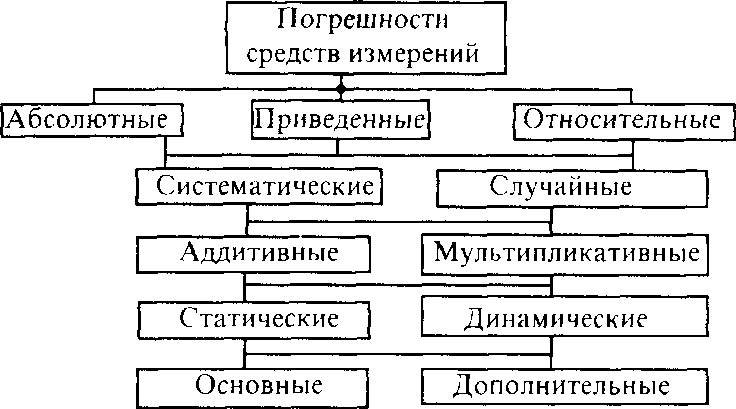
ПОГРЕШНОСТИ ИЗМЕРЕНИЙ. ОБРАБОТКА И ПРЕДСТАВЛЕНИЕ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙПогрешности средств измерений и погрешности измерения. Каждое средство измерения, в том числе и электроизмерительный прибор, характеризуется тем, что отсчитанные по его шкале значения физических величин отличаются от их истинных значений. Разность между этими значениями называется погрешностью средств измерении. Погрешность характеризует точность средства измерения, отражающую близость действительного значения физической величины к обозначенной в паспорте или на шкале прибора. Погрешности средств измерений классифицируют по способу выражения, характеру проявления, зависимостям от текущего значения и режима изменения измеряемой величины, условиям возникновения (рис. 1.2)
Рис. 1.2. Классификация погрешностей средств измерения.
По способу выражения погрешности средств измерений подразделяют на абсолютные, относительные и приведенные. Абсолютная погрешность
Относитечьная погрешность
Приведенная погрешность
Нормирующее значение принимают равным:
а) верхнему пределу рабочей части шкалы для приборов, у которых нулевая отметка находится на краю шкалы или вне ее;  б) арифметической сумме конечных значений диапазона измерений, если нулевая отметка находится внутри шкалы; в) номинальному значению, если прибор предназначен для измерения величин, имеющих номинальные значения; г) длине всей шкалы для приборов с логарифмической или гиперболической шкалой. По характеру проявления погрешности средств измерения подразделяют на систематические и случайные. Систематическая погрешность — погрешность, остающаяся постоянной или изменяющаяся по определенному закону. Ее значение всегда можно учесть введением соответствующих поправок. Случайная погрешность — погрешность, изменяющаяся не по определенному закону, а как центрированная случайная величина. Случайные погрешности нельзя исключить опытным путем. По зависимости от текущего значения измеряемой величиныпогрешности средств измерения делятся нааддитивныеимультипликативные. Аддитивные погрешности не зависят от значения измеряемой величины в пределах диапазона измерения. Источниками их могут быть напряжение смещения в усилителях постоянного тока, шумы элементов схемы, внешние наводки и утечки в схемах, термоЭДС и др. Мультипликативные погрешности пропорциональны текущему значению измеряемой величины. Источниками их являются нестабильность коэффициента передачи отдельных функциональных узлов средств измерения. По зависимости от режима изменения во времени измеряемой величины различают статические и динамические погрешности средств измерения. Статические погрешности возникают при измерении постоянной во времени измеряемой величины (измерение постоянного напряжения, частоты переменного напряжения и т.д.). Динамические погрешности возникают при измерении изменяющихся во времени величин. Причина их появления заключается в инерционности средств измерения, а значение определяется характером изменения измеряемой величины. По зависимости от условий возникновения различают основные и дополнительные погрешности средств измерения.
Основная погрешность — погрешность средств измерения, находя- щихся в нормальных условиях эксплуатации, под которыми понимают нормируемые стандартами температуру внешней среды, влажность, атмосферное давление, напряжение и частоту питания, внешние электрические и магнитные поля и др. Дополнительная погрешность — погрешность средств измерения, возникающая при отклонении одной или более влияющих величин от нормального значения. Обобщенной характеристикой средств измерения, отражающей уровень их точности, является класс точности, определяемый пределами допускаемых основной и дополнительной погрешностей. Следует иметь в виду, что класс точности не является непосредственным показателем точности измерения, выполненного с помощью данного средства. Для электроизмерительных приборов, класс точности которых выражен одним числом[1], основная приведенная погрешность в рабочем диапазоне шкалы, выраженная в процентах, не превышает значения, соответствующего классу точности. Основная абсолютная и относительная погрешности в этом случае представляются в виде
Для приборов, класс точности которых выражается дробью, относительную погрешность определяют по формуле
где с и d — постоянные числа; c/d — класс точности, Измерение любой физической величины сопровождается погрешностями измерения — отклонениями результата измерения от истинного значения измеряемой величины. Численно погрешности измерения выражаются, так же как и погрешности средств измерения, абсолютными
где Погрешности измерения возникают вследствие несовершенства метода измерения, ограниченной точности средств измерений, индивидуальных особенностей экспериментатора. В первом случае погрешности измерения называют методическими. Они являются следствием недостаточной разработанности теории явлений, положенных в основу метода измерения, неточности соотношений, используемых для нахождения измеряемой величины, влияния на режим работы объекта подключаемых средств измерения и др. Во втором случае погрешности измерения называются инструментальными, т.е. погрешностями средств измерения. В третьем случае погрешности измерения называются субъективными Связаны они, как правило, с особенностями органов чувств экспериментатора, его тренированностью и опытом. Любая из перечисленных погрешностей измерения содержит систематическую и случайную, аддитивную и мультипликативную составляющие. Обработка результатов измерений. Обработка результатов измерений имеет цель дать оценку истинному значению измеряемой величины и определить степень достоверности этой оценки. Наиболее достоверным значением измеряемой величины А при наличии только случайных погрешностей и многократном измерении ее является среднеарифметическое
где Оценить точность измерения при этом можно, зная закон распределения случайных погрешностей. Закон нормального распределения случайных погрешностей, наиболее распространенный в практике измерений, математически описывается выражением
Поскольку среднеарифметическое значение А обладает некоторой слу- чайной погрешностью, вводят понятие среднеквадратическои погреш- ности среднеарифметического значения
характеризующее погрешность результата измерения. Из (1.9) видно, что увеличение количества повторных измерений приводит к уменьшению среднеквадратической погрешности Задача 1.1. Аналоговым вольтметром измерено напряжение на выходе двухполюсника и получен отсчет a = 81,6 делений. Выходное сопротивление Температура среды, в которой проводилось измерение, находилось в пределах 20 ± 10°С. Вольтметр имеет следующие характеристики: диапазон измерений от 0 до 10 В; класс точности 0,5; шкала содержит 100 делений; входное сопротивление Решение. Цена деления вольтметра составляет
Отсчет соответствует значению напряжения
Предельное значение модуля основной погрешности
где
Предельное значение абсолютной дополнительной погрешности
Методическая погрешность (погрешность от взаимодействия вольтметра с источником измеряемого напряжения)
Максимальное значение
Минимальное значение
Результирующая предельная погрешность измерения
Ответ.U =8,16 В; Задача 1.2* Аналоговым прибором измеряются напряжение и ток, получен отсчет а. Выходное сопротивление двухполюсника Температура среды, в которой проводились измерения Ɵ. Вольтметр и амперметр имеют следующие характеристики: Таблица 1.1
Задача 1.3. Какие сопротивления можно измерять с погрешностью 1% по схемам рис. 1 3, если сопротивление амперметра не более 10 Ом, а сопротивление вольтметра не менее 10 кОм. Ответ:по схеме рис. 1.3,a Задача 1.4, При поверке амперметра методом сличения (рис.1.4,а)поверяемый прибор показал I = 5,00 А, а образцовый I0 = 5,12 А Нормирующее значение шкал Iном=10 А. Найти абсолютную и приведенную погрешности поверяемого прибора. Ответ Задача 1.5, Результат поверки вольтметра методом сличения (см. рис. 1.4,6) получена табл. 1.2. Определить класс точности поверяемого вольтметра, если его предел измерения U = 150 В
Таблица1.2
Ответ: К=2,5.
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 529. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||
 — разность между показанием прибора А и действительным значением измеряемой величины А:
— разность между показанием прибора А и действительным значением измеряемой величины А: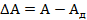 (1.1)
(1.1) — отношение абсолютной погрешности
— отношение абсолютной погрешности  .Обычно относительную погрешность, так же как и приведенную, выражают в процентах:
.Обычно относительную погрешность, так же как и приведенную, выражают в процентах: (1.2)
(1.2) (в процентах) — отношение абсолютной погрешности
(в процентах) — отношение абсолютной погрешности  .
. (1.3)
(1.3) (1.4)
(1.4) (1.5)
(1.5) (1.6)
(1.6)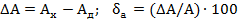 ,
, — действительное значение измеряемой величины;
— действительное значение измеряемой величины;  — результат измерения.
— результат измерения. (1.7)
(1.7) — результаты отдельных измерений; п — число измерений.
— результаты отдельных измерений; п — число измерений. (1.8)
(1.8) — плотность вероятности случайной абсолютной погрешности
— плотность вероятности случайной абсолютной погрешности  —среднеквадратическое отклонение;
—среднеквадратическое отклонение;  — случайное отклонение результата наблюдения от среднеарифметического. Значение
— случайное отклонение результата наблюдения от среднеарифметического. Значение  (1.9)
(1.9) результата измерений, что позволяет дать количественную оценку степени достоверности результата измерения.
результата измерений, что позволяет дать количественную оценку степени достоверности результата измерения. = (10 ± 0,1) кОм. Необходимо представить результат измерения.
= (10 ± 0,1) кОм. Необходимо представить результат измерения. В. ?
В. ? В.
В. ,
, примем равной четверти деления:.
примем равной четверти деления:.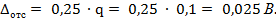
 вызванной отклонением температуры среды от 20°С, согласно ГОСТ 22261-82 не должно превышать основную погрешность на каждые 10°С:
вызванной отклонением температуры среды от 20°С, согласно ГОСТ 22261-82 не должно превышать основную погрешность на каждые 10°С: В.
В.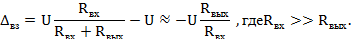
 равно
равно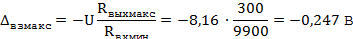
 соответственно будет равно
соответственно будет равно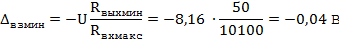
 при вероятности Р = 1 находится как арифметическая сумма составляющих
при вероятности Р = 1 находится как арифметическая сумма составляющих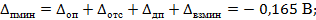
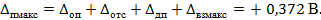
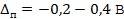 .
. , класс точности,число делений шкал; входные сопротивления
, класс точности,число делений шкал; входные сопротивления  ,
В,А
,
В,А
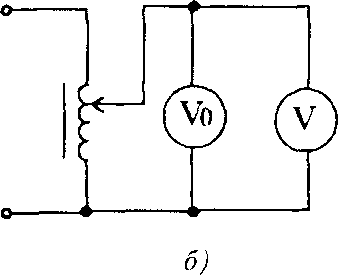
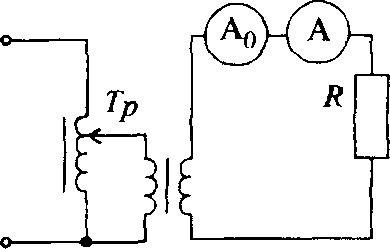
 кОм;по схеме рис 1.3,б
кОм;по схеме рис 1.3,б  0,1 кОм.
0,1 кОм. = — 0,12 А, γ = 1,2%
= — 0,12 А, γ = 1,2%