
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основы теории предельного напряженного состояния (ТПНС) и определение второй критической (предельной) нагрузки
При значительном развитии областей сдвигов, когда грунт близок к разрушению, использование уравнений ТЛДС (4.1) уже невозможно. Здесь необходимо использовать более общие соотношения – дифференциальные уравнения равновесия грунта в точке. Для условий плоской задачи, используя схему и обозначения на рис. 4.2 и приравнивая нулю суммы проекций на координатные оси, получаем: К уравнениям (4.6) присоединяется условие предельного равновесия (2.16), которое следует записать, как и (4.6), через компоненты σx, σz, τ:
Уравнения (4.6) и (4.7) составляют систему уравнений ТПНС для условий плоской задачи. Отыскание напряжений, удовлетворяющих уравнениям (4.6, 4.7), позволяет находить предельную нагрузку на основание, устанавливать устойчивость откосов, определять давление грунта на подпорные стены и т.п. Весь этот круг задач составляет область приложения ТПНС. Задачи ТПНС решаются различными методами: аналитически, с помощью приближенных инженерных приемов и численными методами с преобразованием системы (4.6, 4.7) и заменой производных конечными разностями. Соответствующие решения получены Соколовским В.В., Березанцевым В.Г. и др. Формулы для определения второго критического давления приводятся обычно к трехчленной форме, как и (4.5).  На основе анализа и обобщения решений ТПНС с учетом опытных данных в нормах проектирования принята следующая формула для предельного давления на основание внецентренно нагруженного фундамента произвольной формы: где Nγ, Nq, Nc – коэффициенты несущей способности, определяемые по табл. 4.1 в зависимости от расчетного значения φI и угла наклона равнодействующей нагрузки к вертикали δ; γI и γ΄I – расчетные значения удельного веса грунта под подошвой в пределах глубины заложения фундамента d; ξγ, ξq, ξc – коэффициенты формы подошвы фундамента (для ленточного фундамента ξγ=ξq=ξc=1); b΄ – приведенная ширина подошвы фундамента. Таблица 4.1 Значения коэффициентов несущей способности в формуле (4.8)
где При возможности возникновения нестабилизированного состояния основания коэффициенты Nγ, Nq, Nc в (4.8) берутся при φI = 0.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 345. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 (4.6)
(4.6)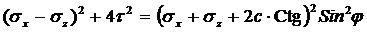 . (4.7)
. (4.7)
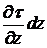



 , (4.8)
, (4.8)




 ,
где b΄,ℓ΄– приведенные, т.е. уменьшенные на величину двойного эксцентриситета нагрузки размеры подошвы фундамента:
b΄= b-2ex ; l΄= l-2ey,
где ex, ey – эксцентриситеты (рис. 4.3)
Коэффициенты формы определяются по формулам:
,
где b΄,ℓ΄– приведенные, т.е. уменьшенные на величину двойного эксцентриситета нагрузки размеры подошвы фундамента:
b΄= b-2ex ; l΄= l-2ey,
где ex, ey – эксцентриситеты (рис. 4.3)
Коэффициенты формы определяются по формулам:


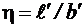 – отношение приведенных сторон подошвы.
– отношение приведенных сторон подошвы.