
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Напряжения от полосовой равномерно распределенной нагрузки
Грунт работает в условиях плоской задачи. При этом нормальное напряжение вдоль оси у постоянно, касательные в плоскости xz отсутствуют и напряженное состояние в осях xoz характеризуется: Очевидно, что для этого случая можно также использовать формулу (3.3), принимая α по последнему столбцу табл. 3.2. Однако здесь целесообразно привести простые формулы для главных напряжений
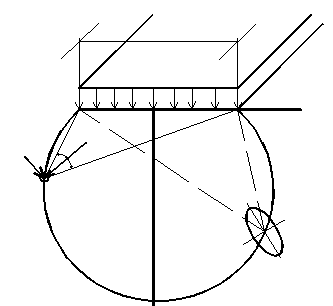
При этом в точках на осевой вертикали в силу симметрии будет где 2β – угол, под которым видны края полосы из т. М (угол видимости). Большее напряжение Из формулы (3.4) очевиден вид изолиний главных напряжений: это окружности с центром на оси z , проходящие через т. М и края полосы. Во всех точках 2β = const, поскольку угол опирается на одну и ту же хорду – загруженную полосу шириной b. Напряженное состояние в любой точке удобно характеризовать эллипсом напряжений (см. рис. 3.4). Если сравнить изменение напряжений с глубиной от одинаковой нагрузки р, действующей на квадратной или круговой площадке и на полосе той же ширины, то обнаруживается более медленное затухание (убывание) напряжений от полосовой нагрузки (рис. 3.4). Учет этого фактора особенно важен, если на некоторой глубине в основании оказывается прослоек слабого грунта. 
Напряжения от собственного веса грунта
Напряжения, рассчитанные по приведенным ранее формулам, добавляются к природным напряжениям от собственного веса грунта. Вертикальное сжимающее напряжение в грунте с удельным весом γ на глубине z определяется по формуле: Если основание слоистое и удельный вес каждого слоя γi, а мощности слоев hi , то напряжения по (3.5) суммируются, так что на подошве i-го слоя σi будет равно: Эпюра напряжений представляется ломаной; точки излома – на границе слоев. Ниже уровня подземных вод следует в (3.6) удельный вес γзв принимать по (1.7) с учетом взвешивания грунта. На кровле подстилающего водонепроницаемого слоя (водоупора) в этом случае эпюра Горизонтальные нормальные напряжения определяются по формуле:
 , (3.7) , (3.7)
где ξ – коэффициент бокового давления, зависящий от вида и состояния грунта. Обычно принимается значение ξ по (2.3), а для мягко-, текучепластичных глинистых грунтов можно принять ξ=1.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 371. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,
,  ,
,  . Такое напряженное состояние возникает под ленточными фундаментами стен, насыпями земляного полотна и др. Расчетная схема приведена на рис. 3.4. Требуется определить напряжения в произвольной точке М.
. Такое напряженное состояние возникает под ленточными фундаментами стен, насыпями земляного полотна и др. Расчетная схема приведена на рис. 3.4. Требуется определить напряжения в произвольной точке М. ,
,  .
.
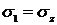 и
и  . Главные напряжения равны:
. Главные напряжения равны: , (3.4)
, (3.4)
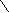

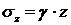 . (3.5)
. (3.5) . (3.6)
. (3.6)







