
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Основні геометричні параметри циліндричних зубчастих передач
Розглянемо основні елементи зубчастого колеса (рис. 9.5, а). Циліндрична поверхня (1), що відокремлюєзубці від тіла зубчастого колеса, називається поверхнею западин зубців. Циліндрична поверхня (2), що обмежує зуби по висоті – поверхня вершин зубців. Простір між двома сусідніми зубцями (3) – западина. Поверхня, що обмежує зуб зі сторони западини (4), називається бічною поверхнею зуба.
а) б) Рис. 9.5
Бічна поверхня складається із головної (5) та перехідної (6) поверхонь. Головна поверхня – це та частина бокової поверхні зуба, яка взаємодіє з головною поверхнею іншого зуба і при цьому забезпечує задане передаточне відношення. Перехідна поверхня з’єднує головну поверхню з поверхнею западин. Головною поверхнею, як зазначалось вище, найчастіше є евольвентна поверхня. Її можна подати як сукупність цілком однакових евольвент, що розміщені у площинах, перпендикулярних до осі колеса. Ці евольвенти є траєкторіями точок твірної прямої На рис. 9.6 зображено зубчасте колесо із зовнішніми зубцями. При розгляді зубчастих коліс зазначають чотири кола: – коло вершин (виступів, зовнішнє коло), – коло западин, – основне коло,  – ділильне коло, Рис. 9.6 Коли мова йде про зачеплення зубчастих коліс, розрізняють ще початкове коло. Початкове коло – це поняття кінематичне і у окремо взятого колеса такого кола не має. Початкові кола, як вже відмічалось, це центроїди у відносному русі зубчастих коліс, тобто кола, якими зубчасті колеса у відносному русі перекочуються одне по одному без ковзання. Для зачеплення нормальних, нульових коліс, радіуси початкових кіл дорівнюють радіусам ділильних кіл, Відстань між однойменними точками профілів двох сусідніх зубців по дузі концентричного кола зубчастого колеса називається коловим кроком зубців і позначається р (з індексом відповідного кола). Розрізняють ділильний р, початковий рw, основний рb та інші колові кроки зубців, що відповідають ділильному, початковому, основному та іншим концентричним колам зубчастого колеса. Крок зубців по будь-якому колу можна представити як суму товщини зуба s та ширини западини е; тобто р=s+e; рі=sі+еі Дуги р, рb, рw та рі відповідають одному і тому ж кутовому кроку
Центральний кут, що опирається на дугу кола зубчастого колеса, яка дорівнює коловому кроку називається кутовим кроком. Кутовий крок можна виразити і так
Важливим елементом зубчастого колеса є крок по ділильному колу. Виразимо довжину ділильного кола через крок р і число зубців z: 2p r = p z або
Відношення р /p позначають буквою m і називають модулем. Це зв’язано з тим, що p – число ірраціональне (3,1459…), і відношення р /p не може бути точно пораховане. Цей факт ускладнює підбір розмірів зубчастих коліс при проектуванні коліс та практичний їх вимір. З іншого боку, зубці коліс нарізаються на спеціальних станках ріжучим інструментом, розміри і форма якого залежать від величини модуля. Щоб не мати на заводах надмірної кількості ріжучого інструменту, домовились для деякого кола, що називається ділильним, вибирати модулі із ряду раціональних чисел. Модулі зубців стандартизовані. У ГОСТ 9563 наведено значення модулів, починаючи від 0,05 до 100 мм, у вигляді двох рядів (основного та допоміжного). До цих значень можуть заокруглюватись модулі, що отримані при розрахунку. Модуль є основною характеристикою зубчастих коліс. Через модуль виражають розміри зубчастих коліс, передач та зубонарізного інструменту. Модуль – це крок на ділильному колі, поділений на p. Одиниця модуля – мм. Стандартні модулі від 1 до 5 мм такі: 1-й ряд: 1 1,25 1,5 2 2,5 3 4 5 2-й ряд: 1,125 1,375 1,75 2,25 2,75 3,5 4,5 5,5 Радіальна відстань h між колами вершин та западин є висотою зуба; вона складається із двох частин: висоти головки ha та висоти ніжки hf. Тобто, h = ha+hf. Визначимо розміри зубчастих коліс, у яких ділильні кола співпадають з початковими; такі колеса будемо називати нульовими. Ці розміри, як зазначалося, можуть бути завжди виражені у функції модуля. Наприклад, ділильний діаметр d = mz. Діаметр вершин
Діаметр западин
Тут враховано, що висота ha головки зуба та висота hf ніжки зуба переважно приймаються рівними ha=m, hf=1,25m. Більший розмір ніжки у порівнянні з головкою забезпечує зазор між головкою зуба одного колеса та впадиною іншого. Відзначимо, що деколи застосовуються колеса з вкороченими зубцями, для яких ha=0,8m, hf=m. Міжосьова відстань
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 412. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


 , що належить площині Н, яка перекочується по основному циліндру без ковзання (рис. 9.5, б).
, що належить площині Н, яка перекочується по основному циліндру без ковзання (рис. 9.5, б).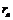 – коло, що належить поверхні вершин;
– коло, що належить поверхні вершин; – коло, що належить поверхні западин;
– коло, що належить поверхні западин; – коло, яке є базою для побудови евольвентного профілю зубців. Діаметр основного кола – єдиний параметр, що визначає форму евольвенти, оскільки кожному конкретному колу відповідає одна певна евольвента;
– коло, яке є базою для побудови евольвентного профілю зубців. Діаметр основного кола – єдиний параметр, що визначає форму евольвенти, оскільки кожному конкретному колу відповідає одна певна евольвента;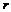 – коло, яке є базою для визначення розмірів елементів зубців. Ділильне коло, це коло, що перетинає профіль зуба в точці, для якої кут профілю дорівнює стандартному куту, a=20° (куту нахилу зуба інструментальної рейки). Нагадаємо, гострий кут у поперечному перерізі зубця, між дотичною до профілю зубця у даній точці та лінією, що проходить через цю точку і центр колеса, називається кутом профілю зубця. Кут профілю зубця у т.К, яка знаходиться на ділильному колі, стандартизований і дорівнює 20°. Ділильне коло ділить зубець на дві частини – головку
– коло, яке є базою для визначення розмірів елементів зубців. Ділильне коло, це коло, що перетинає профіль зуба в точці, для якої кут профілю дорівнює стандартному куту, a=20° (куту нахилу зуба інструментальної рейки). Нагадаємо, гострий кут у поперечному перерізі зубця, між дотичною до профілю зубця у даній точці та лінією, що проходить через цю точку і центр колеса, називається кутом профілю зубця. Кут профілю зубця у т.К, яка знаходиться на ділильному колі, стандартизований і дорівнює 20°. Ділильне коло ділить зубець на дві частини – головку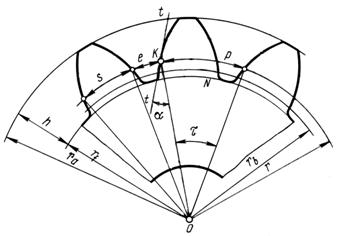 та ніжку.
та ніжку.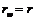 .
. .
. .
. .
. .
. .
. між центрами коліс О1 та О2 також може бути виражена через m
між центрами коліс О1 та О2 також може бути виражена через m .
.