
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Евольвента кола, її властивості та рівняння
Евольвентою кола називається крива, яку описує будь-яка точка прямої, що перекочується по колу без ковзання. Пряму, що перекочується, називають твірною або відтворюючою прямою, вона являє собою рухому центроїду, а коло, відповідно, є нерухомою центроїдою. При перекочуванні за годинниковою стрілкою дотичної прямої n-n по колу Детально побудову евольвенти основного кола rв,при перекочуванні по ньому твірної прямої n-n, розглянемо на занятті з курсового проектування при побудові картини зубчастого зачеплення. Рівняння евольвенти. Із умови утворення евольвенти довжина відрізка КуNу (радіус кривини евольвенти в т. Кy) повинна бути рівна дузі, що розгортається NyKy= rв(qу+aу)=rвtgaу, або inv aу=qу=tgaу-aу, (3) де aу – кут профілю, гострий кут між дотичною до евольвенти (до профілю зуба) у т. Ку і її радіусом вектором ОКу; qу – евольвентний кут – кут, утворений початковим радіус-вектором ОК0 та біжучим радіус-вектором ОКу. Тригонометричну функцію кута aу – qу=tgaу-aу називають евольвентною функцією, позначають скорочено inv (інвалюта) та використовують при геометричному розрахунку евольвентних зубчастих коліс. Для спрощення розрахунків значення invaу наводяться у таблицях для різних значень кута aу. 
Рис. 9.4
Будь-яка т. Ку евольвенти повністю визначається двома параметрами: радіус-вектором ry та евольвентним кутом qу. Зв’язок між ry та кутом aу встановлюється з DNyОКу залежністю ry=rв/соsaу (4) Формули (3) та (4) визначають рівняння евольвенти в полярних координатах ry і qу. Ці рівняння, після виключення параметра aу, вказують на те, що евольвента повністю визначається основним колом. Для теорії зачеплення важливе значення мають такі основні властивості евольвенти: - евольвента являє собою симетричну криву, що має дві вітки, які збігаються у початковій точці К0, розміщеній на основному колі. Отже, евольвента не має точок всередині основного кола; - точки Nу є миттєвими центрами швидкостей твірної прямої n-n і центрами кривини евольвенти у точках Ку. Отже, нормалі до евольвенти в будь-якій точці є прямі, що дотичні до основного кола у відповідних точках; - основне коло є геометричним місцем центрів кривини евольвенти, що описують твірні прямі, тому відрізки NуКу є радіусами кривини евольвенти у відповідних точках Ку; - кут профілю aу та радіус кривини ry евольвенти у початковій точці К0 дорівнюють нулю. По мірі віддалення точок евольвенти від основного кола, кут профілю збільшується, кривина евольвенти зменшується, тобто радіус кривини збільшується; - при збільшенні радіуса основного кола евольвентний профіль поступово втрачає свою кривину і при rв=¥ евольвента перетворюється на пряму лінію. Отже, щоб визначити радіус кривини евольвенти (зубця) у певній точці треба провести від неї дотичну до основного кола.
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 380. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , т. К0 вказаної прямої опише евольвенту К0Ку (рис. 9.4). Зазначимо, що при перекочуванні даної прямої у протилежному напрямі т. К0 опише також евольвенту,
, т. К0 вказаної прямої опише евольвенту К0Ку (рис. 9.4). Зазначимо, що при перекочуванні даної прямої у протилежному напрямі т. К0 опише також евольвенту,  (точніше ліву вітку евольвенти). Оскільки пряма перекочується без ковзання, справедлива рівність NнKy=
(точніше ліву вітку евольвенти). Оскільки пряма перекочується без ковзання, справедлива рівність NнKy= 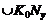 . Наведемо також інші визначення. Геометричне місце центрів кривини якої-небудь кривої називається еволютою, а сама крива по відношенню до еволюти – розгортка або евольвента. Отже, евольвента кола є крива, центри кривини якої лежать на колі. В теорії зачеплення це коло називають основним, оскільки воно служить основою для побудови евольвенти, і позначають завжди з індексом в, тобто, rв. Отже, основне коло – коло, евольвентою якого є профіль зуба.
. Наведемо також інші визначення. Геометричне місце центрів кривини якої-небудь кривої називається еволютою, а сама крива по відношенню до еволюти – розгортка або евольвента. Отже, евольвента кола є крива, центри кривини якої лежать на колі. В теорії зачеплення це коло називають основним, оскільки воно служить основою для побудови евольвенти, і позначають завжди з індексом в, тобто, rв. Отже, основне коло – коло, евольвентою якого є профіль зуба.